Los sólidos platónicos

Los sólidos platónicos son poliedros convexos en los que todas sus caras son polígonos regulares iguales entre sí, y en los que sus ángulos son iguales. Reciben este nombre en honor al filósofo griego Platón a quien se le atribuye el hecho de haberlos estudiado en primera instancia.

En todos los vértices de un sólido platónico existen el mismo número de caras y de aristas. Además, todas las aristas de un sólido platónico tienen la misma longitud. Estos cinco sólidos son: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro.

El tetraedro

El tetraedro es un sólido platónico que tiene todas sus caras con forma triangular. Esta figura también es conocida como pirámide triangular. Los cuatro vértices del tetraedro se encuentran a la misma distancia los unos de los otros.

El tetraedro

El cubo

El cubo es un sólido platónico que tiene todas sus caras con forma cuadrada. Tiene seis caras idénticas,12 aristas y 8 vértices. Las caras opuestas de un cubo son paralelas entre sí.

El cubo

El octaedro

El octaedro es un sólido platónico que tiene todas sus caras con forma triangular.  Un octaedro tiene 8 caras triangulares, 12 aristas y 6 vértices. Esta figura tiene la forma de una pirámide cuadrada doble. Cada una de las caras del octaedro se encuentra con otras tres caras. Además, cuatro caras confluyen en cada vértice.

El octaedro

El dodecaedro

El dodecaedro tiene todas sus caras con forma pentagonal. Un dodecaedro tiene 12 caras, 30 aristas y 20 vértices. Tres caras pentagonales se encuentran en cada vértice.

El dodecaedro

El icosaedro

El icosaedro tiene todas sus caras con forma triangular. Los icosaedros tienen 20 caras, 30 aristas y 12 vértices. Es el sólido platónico con el mayor número de caras.

El icosaedro

 

PROPIEDADES SIMÉTRICAS

Los sólidos platónicos tienen algunas características simétricas:

• Tienen un punto (centro de simetría) que equidista de sus caras, de sus vértices y de sus aristas.
• Disponen de simetría axialrespecto a una serie de ejes de simetría que pasan por el centro de simetría anterior.
• Todos ellos tienen también simetría especular respecto a una serie de planos de simetría que los dividen en dos partes iguales.

 

LAS RAZONES DE SU RECONOCIMIENTO

Estas cinco figuras son quizá las más conocidas de todas las que existen en el mundo de la geometría tridimensional. Hay varias razones por las que se han hecho muy famosas y vamos a intentar exponer los diferentes puntos por los que han sido tan conocidas.

1. Simetría y estética: los sólidos platónicos son altamente simétricos y tienen formas geométricas muy armoniosas. Esta simetría ha fascinado a matemáticos, artistas y arquitectos a lo largo de la historia.

2. Historia y filosofía: su estudio se remonta a la antigua Grecia, donde Platón los asoció con los elementos fundamentales del universo. Esta conexión filosófica les otorgó un significado profundo en la cosmología y la filosofía de la época.

3. Matemáticas y geometría: los sólidos platónicos son un tema central en la geometría, y su estudio ha contribuido a muchas áreas de las matemáticas.  Son ejemplos de poliedros regulares, lo que significa que sus caras son polígonos regulares idénticos y tienen la misma disposición en cada vértice.

4. Cultura popular: los sólidos platónicos han aparecido en diversas formas en la cultura popular, desde el arte hasta los videojuegos, lo que ha contribuido a su reconocimiento. Su formas icónicas son fácilmente reconocibles y se utilizan en diversas aplicaciones estéticas.

5. Educación: en la educación matemática, los sólidos platónicos son una herramienta útil para enseñar conceptos de geometría, simetría y poliedros.

6. Simbolismo geométrico: los sólidos platónicos son vistos como representaciones de la armonía y el orden en el universo. Su perfección geométrica ha llevado a muchos a asociarlos con la idea de un cosmos ordenado y divino.

7. Conexiones místicas: en diversas tradiciones esotéricas y místicas, los sólidos platónicos son considerados portadores de significados profundos. Se les asocia con la meditación, la búsqueda de la verdad y la conexión con lo divino. En la geometría sagrada, se les atribuye un papel en la comprensión del universo.

8. Armonía musical: algunos estudiosos también han explorado la relación entre la geometría de los sólidos platónicos y las proporciones musicales, sugiriendo que su estructura puede reflejar principios de armonía que trascienden lo físico.

En resumen, la combinación de su perfección matemática, su conexión con los elementos naturales y su simbolismo en diversas tradiciones espirituales han hecho que los sólidos platónicos sean considerados como algo más que simples figuras geométricas, convirtiéndose en un puente entre la matemática, la filosofía, la naturaleza y la espiritualidad.

 

LOS CINCO SÓLIDOS PLATÓNICOS Y EL CUBO DE METATRON

Aparte de todas estas características que hemos nombrado, hay otra que relaciona a estos sólidos directamente con la geometría sagrada ya que todos estos sólidos platónicos se pueden dibujar remarcando algunos trazos existentes en el Cubo de Metatron.

Hemos visto en otros artículos como desde el Cubo de Metatron aparecían la Semilla de la vida, el Merkabah, la Estrella de David y el Rombo. Pero ahora podemos ir un poco más hacia adelante y comprobar como desde el Cubo de Metatron podemos obtener también la representación bidimensional de los cinco sólidos platónicos.

Para ello hemos de partir de la figura convencional del Cubo de Metatron (en la que podemos observar la estrella de David azul) y girarla 90º a la izquierda, con lo que obtendremos una estrella de David roja. A partir de aquí si fundimos la estrella azul y la roja, obtendremos una nueva figura geométrica que representa a los dos Cubos de Metatron girados 90º y unidos. Desde este nueva figura podremos trazar distintas líneas y encontrar con ello a la totalidad de los sólidos platónicos.

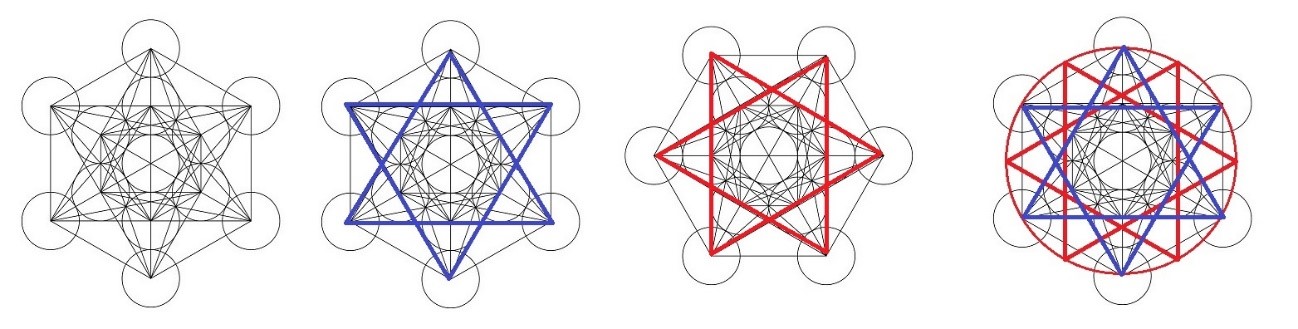
Los dos Cubos de Metatron unidos

Como vemos, la figura resultante de esta fusión es un doble Cubo de Metatron, en el que se construye una estrella de 12 puntas que será la que nos va a permitir encontrar a los cinco sólidos en su interior. Las tres primeras figuras de las cinco existentes las podemos hallar con la presencia de un solo Cubo de Metatron, pero para poder encontrar y dibujar a las dos últimas y más complejas, vamos a necesitar las líneas que nos proporcionan los dos Cubos de Metatron fusionados.

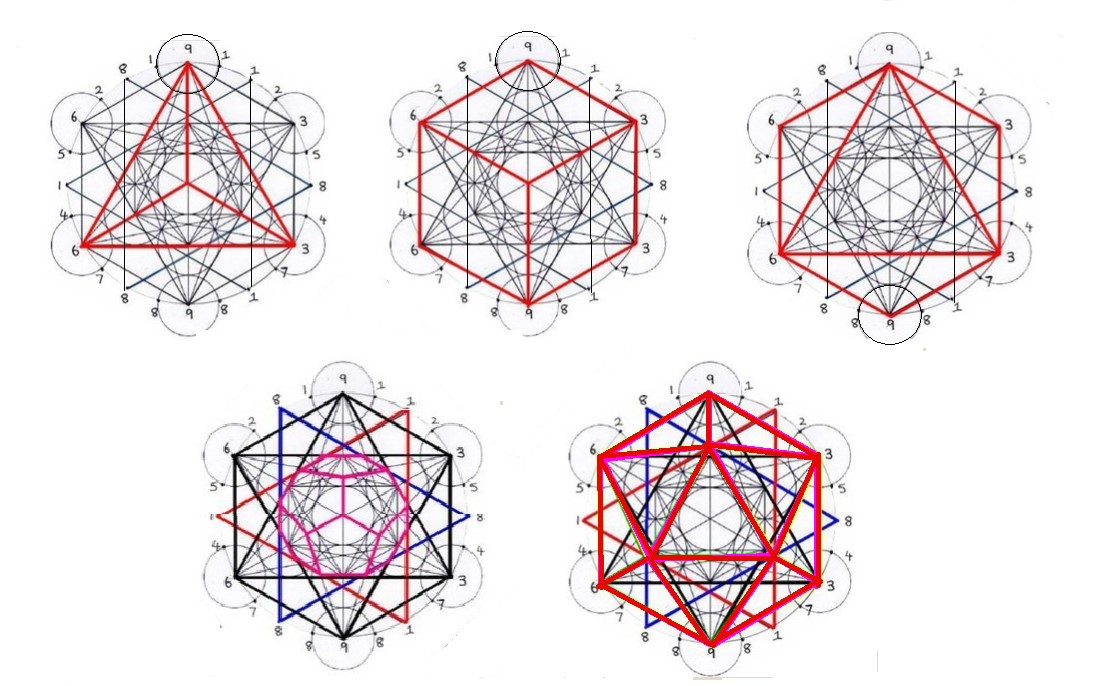
Los cinco sólidos platónicos dentro del doble Metatron

Para verlos de una manera más clara, pondremos en una misma imagen el sólido platónico dentro del esquema de la geometría sagrada en el que participa el Rombo y a su derecha, el dibujo más esquemático. En este primer ejemplo, podemos ver al tetraedro que emerge dentro del Cubo de Metatron y donde observamos también al Rombo y la Semilla de la vida.

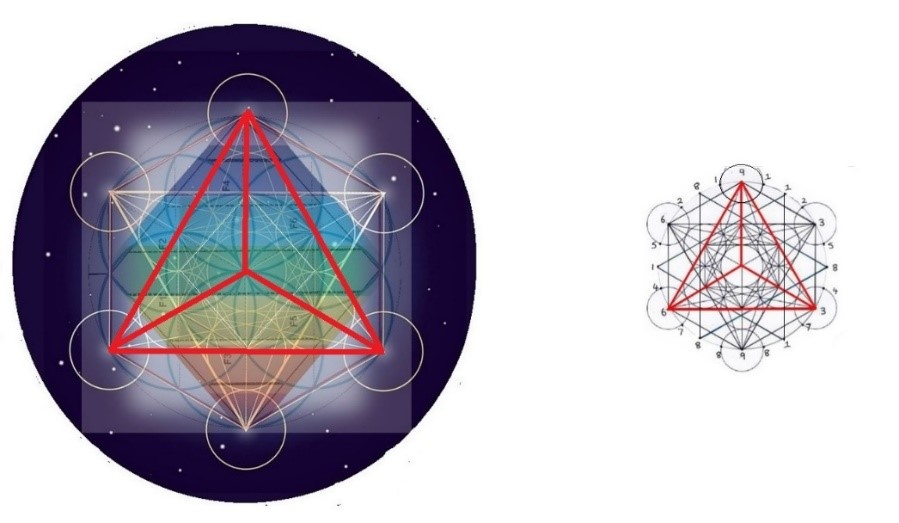
Tetraedro dentro del Cubo de Metatron

En este segundo dibujo, veremos cómo se origina el cubo utilizando algunos trazos dentro de la geometría compleja del Cubo de Metatron. También podemos ver a la figura simplificada a su derecha.

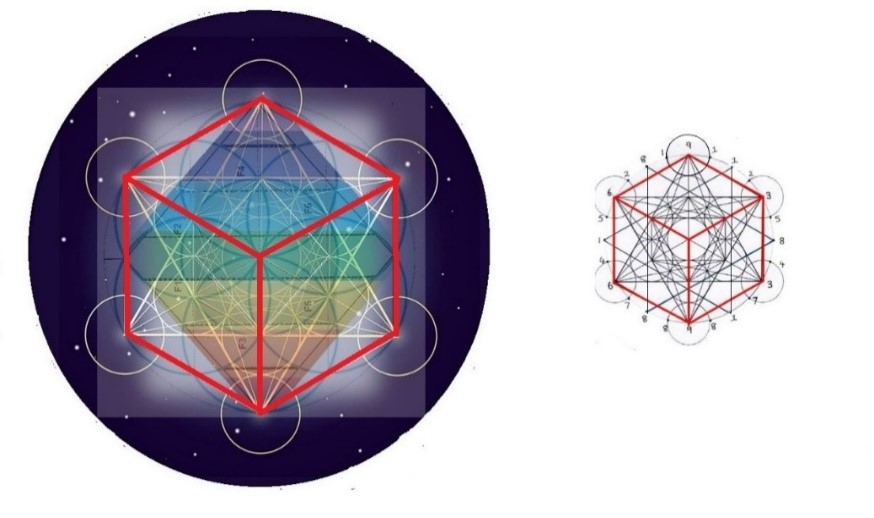
Cubo dentro de Metatron

El tercer dibujo de la serie es el que corresponde al octaedro. Como podemos ver, el octaedro se obtiene también con algunos trazos del Metatron inicial.

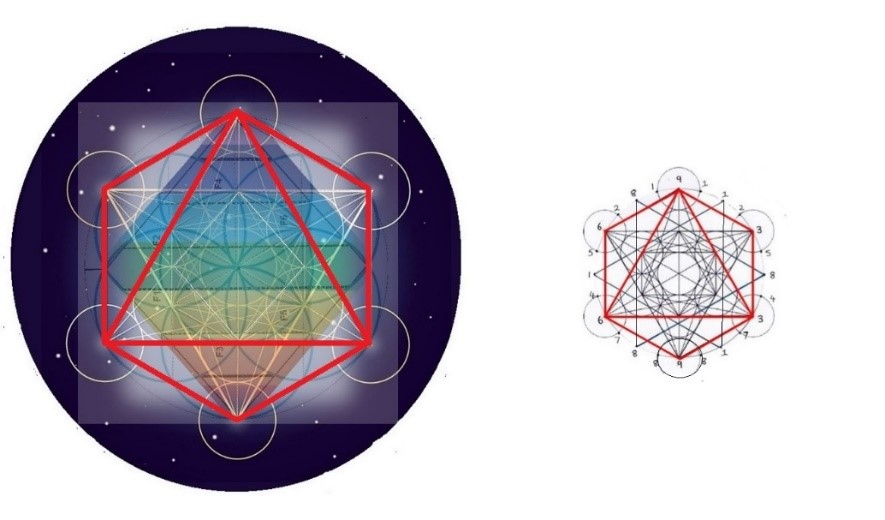
Octaedro dentro de Metatron

Y ahora toca empezar a trabajar con los sólidos más complejos. Para poder visualizar el dodecaedro y el icosaedro, debemos realizar la fusión de las dos estrellas de David y a partir de aquí, nos aparecerán todas las líneas que permitirán dibujar con posterioridad a estos sólidos en dos dimensiones. En las figuras anteriores que eran de más fácil construcción, no era necesario realizar esta fusión y se podían obtener desde un solo Cubo de Metatron.  A partir de ahora es preciso realizar esta unión para que aparezcan todas las líneas que van a permitir encontrar a estas dos figuras platónicas.

Empezaremos con el dodecaedro. Con un poco de paciencia iremos viendo como aprovechando algunos fragmentos de todas las líneas que aparecen, irán emergiendo todas las aristas del sólido tridimensional proyectado en dos dimensiones.

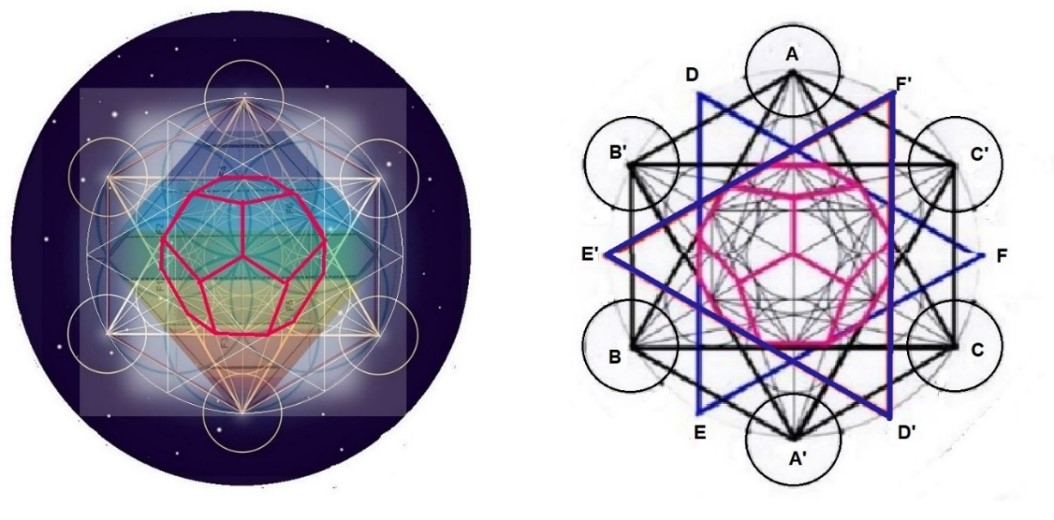
Dodecaedro dentro del doble Cubo de Metatron

Y por último nos aparecería el icosaedro, la figura más compleja de la serie para la cual también necesitamos de los dos Cubos de Metatron.

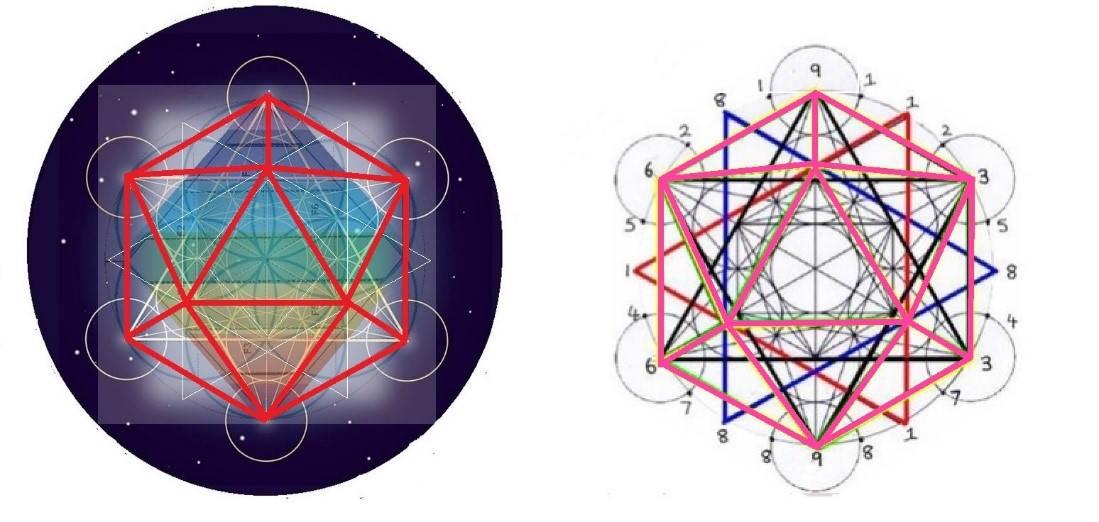
Icosaedro dentro del doble Cubo de Metatron

 

LA ESTRELLA DE 12 PUNTAS

La estrella de 12 puntas que aparece como el resultado de la fusión de dos Cubos de Metatron es de una belleza asombrosa. En esta unión se hace visible una curiosa figura romboidal situada en la parte central con cuatro aristas semi-arqueadas que recuerda a un cometa. Además, podemos ver también a los 12 círculos exteriores cuyos centros están en los 12 vértices de la estrella de 12 puntas.

También podemos apreciar un doble degradado cromático pues en el Rombo horizontal, el color rojo está a la izquierda y el violeta a la derecha. Y en el Rombo vertical, el color rojo se halla en la parte inferior y el violeta en la superior.

En la parte central de la figura podemos observar a una cruz que nos recuerda a la cruz de la vida en la que se observa el equilibrio entre arriba-abajo (Cielo-Tierra) y derecha-izquierda (Yin-Yang).

Y en la parte más central de la figura se observa esta preciosa margarita de 12 pétalos dentro de la cual existe otra margarita menor con la misma estructura dodecagrámica.

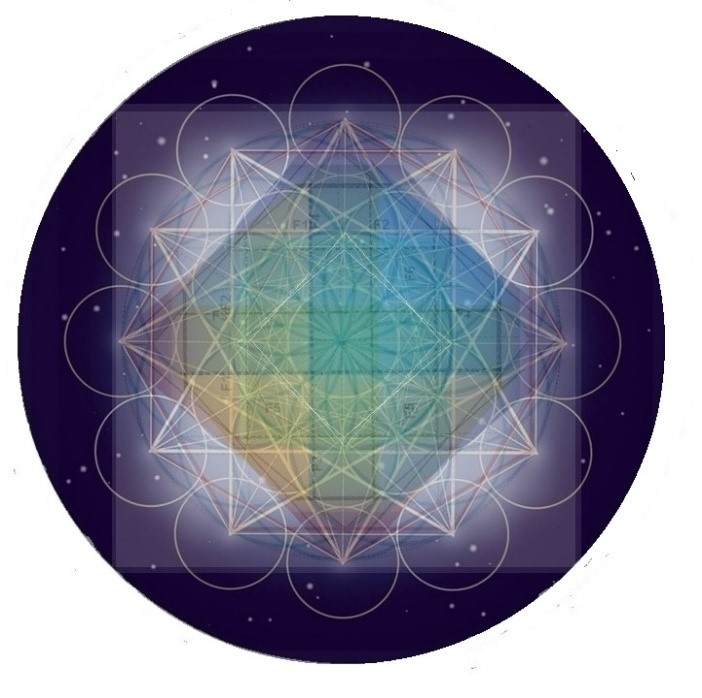
La complejidad del doble Metatron

Otra de las cuestiones que llama la atención en este doble Cubo de Metatron es que la circunferencia que lo contiene todo está constituida a su vez por 12 círculos menores exteriores que contactan el uno con el otro.

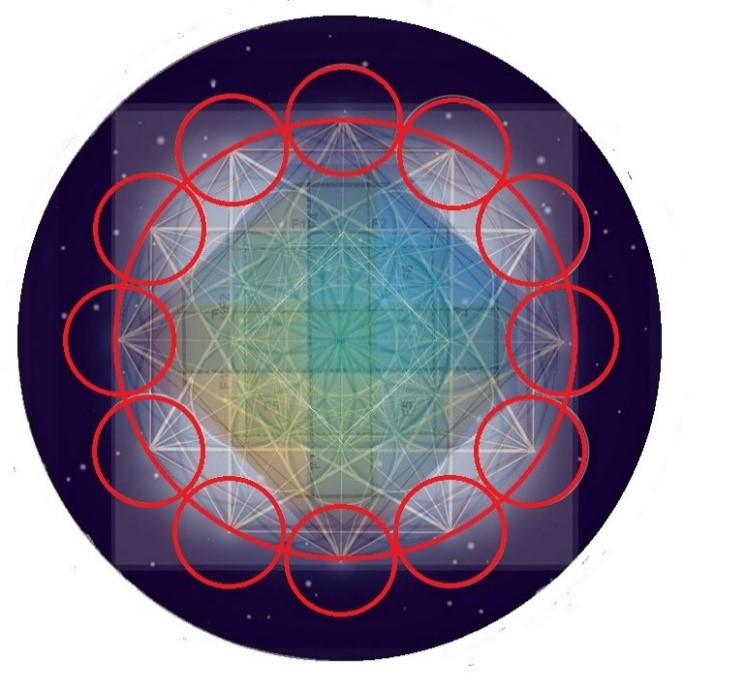
Las 12 circunferencias menores forman la mayor

Y si bien estas 12 circunferencias se encuentran en el exterior, también en el interior encontramos a otras 12 que están vinculadas geométricamente con las exteriores en relación 1:1.

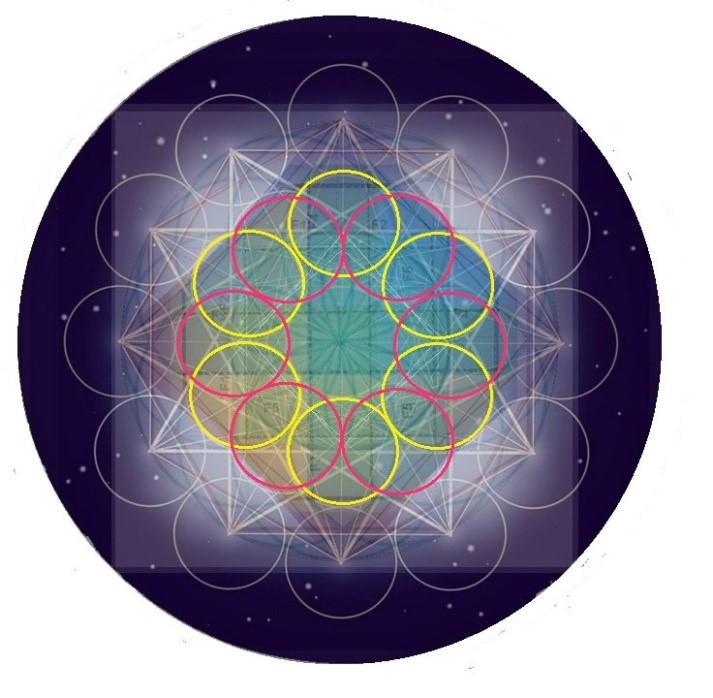
Las 12 circunferencias interiores

El número 12 es una cifra que está totalmente vinculada al Rombo desde sus inicios más remotos. El principio holográfico hace que dentro de cada unidad de esa docena primordial se encuentre a su vez otra docena interior en un proceso que se repite indefinidamente.

Por otro lado, el centro radial del que todo emana extiende sus 12 raíces que darán origen a todo lo creado. Por fuera de esta primera margarita enmarcada en el círculo dorado se encuentra otra margarita que la abraza y que parece ser otro nivel de expresión de esta misma estructura.

La estructura del centro

Todo parte del centro y desde la circunferencia exterior (su obra) y a través de la geometría se vuelve a llegar al centro y a descubrir la naturaleza creadora de ese centro radial. Esto es un bello principio filosófico y universal expresado de una manera hermosa y geométrica con los elementos más básicos de la geometría: la circunferencia y la línea.

La geometría habla en un lenguaje que no entiende de culturas, razas, credos o filosofías. Es un lenguaje universal y ciertamente puede ser difícil de entender para aquel que no sabe las claves de su lectura. Pero si por ventura se conoce el mensaje que se quiere transmitir con el dibujo, entonces se le puede ver allí, oculto, agazapado y hablando sutilmente entre el mar de líneas y circunferencias que construyen estas sagradas figuras geométricas. Son verdades expresadas en símbolos. Bellos mandalas que revelan conocimientos.

Los cinco sólidos platónicos, esas cinco figuras relacionadas con los elementos de la naturaleza, la creación, el Creador y su obra están totalmente vinculadas al Rombo. De alguna manera, estas cinco figuras debían hacerse visibles para poder ser observadas dentro del Rombo y las estructuras que lo mantienen, protegen y envuelven. Y hoy lo han hecho. Bienvenidas!

Geometría sagrada dentro de geometría sagrada.