18-19 (2ª parte)
Es un artículo que salió publicado en el 2010, aunque los 10 dibujos que componen la serie se realizaron cuatro años antes. No se publicaron en aquel momento, porque ya no eran necesarios para demostrar lo que se andaba buscando, que era el tamaño de la diagonal menor. Este dato en concreto se había conseguido ya con la primera serie de dibujos. Como parecía que estos segundos dibujos eran solamente un estudio estético y geométrico sin un valor claramente definido, se quedaron en un cajón a la espera de algún día, poder ser sacados a la luz.
Cuando escribí el artículo 18-19 1ª parte, me quedaron en el tintero algunos dibujos más por publicar. Estaban todos inacabados, porque el material del que disponía en el primer artículo, ya me sirvió suficientemente para aclarar la incógnita de la medida de la dimensión menor del Rombo. A partir de ese momento, los dibujos inconclusos, perdieron casi todo su valor de investigación. Algunos, ya sólo eran recreaciones geométricas que venían siempre a decir lo mismo. Todos hablaban de la estructura interna y me iban apareciendo los mismos datos que se iban repitiendo una y otra vez. Eran dibujos que ya habían conseguido su finalidad y no me aportaban nuevas conclusiones.
Fue por eso por lo que los dejé sin acabar. Se quedaron en una carpeta. Estaban prácticamente finalizados, pero no llegaron a ver la luz. Ahora, mucho más tarde, siento que deben aparecer. No todos seguramente, pero si, algunos de ellos. Estos dibujos, tienen más bien un valor anecdótico, lo sé, pero me sabe mal que se tiñan de amarillo con el paso del tiempo. Parece que reclamen el derecho a salir del ostracismo al que les llevó el éxito de sus hermanos.
A pesar de todo lo que he dicho, los dibujos, siguen aportando datos valiosos y alguno de ellos, plantea sugerencias muy interesantes respecto al funcionamiento de la SFR.
Ahora, os dejo en compañía de estos viejos amigos.
La estrella de mar
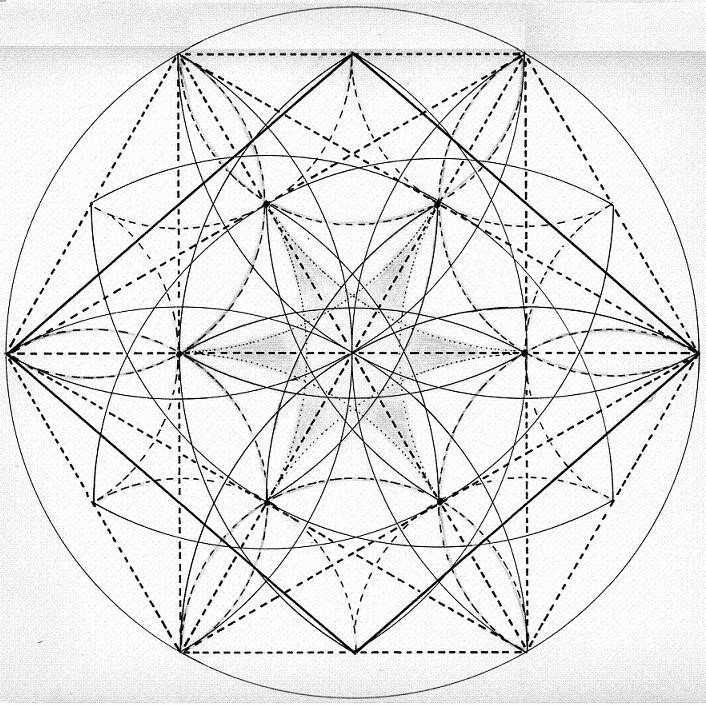
Dibujo
El hexágono interior se puede encontrar por las bisectrices del hexágono exterior. También se puede hallar a partir de los puntos medios del hexágono exterior. Incluso desde las aristas del hexágono exterior, o desde la rotación del Rombo tridimensional visto desde arriba, y que está representado por triángulos equiláteros.
Hexágonos concéntricos
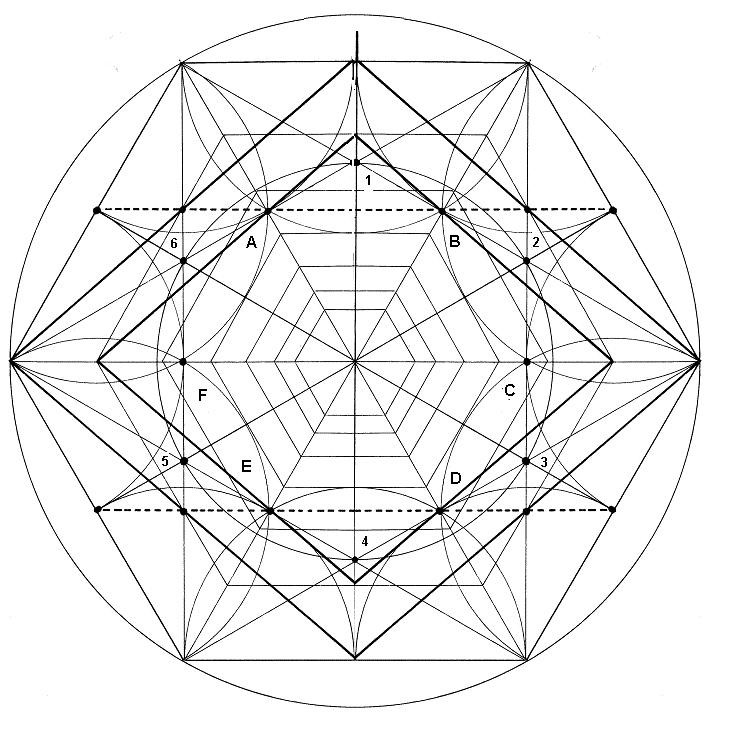
Dibujo
Creación del hexágono interior. Se puede conseguir desde el hexágono exterior y desde los triángulos que forma el rombo tridimensional visto desde arriba. Se observan también los ejes horizontales. Se construyen hexágonos concéntricos donde se puede construir el Rombo. Puede proporcionar una imagen de rombos concéntricos, crecientes o decrecientes.
Hexágonos concéntricos con color
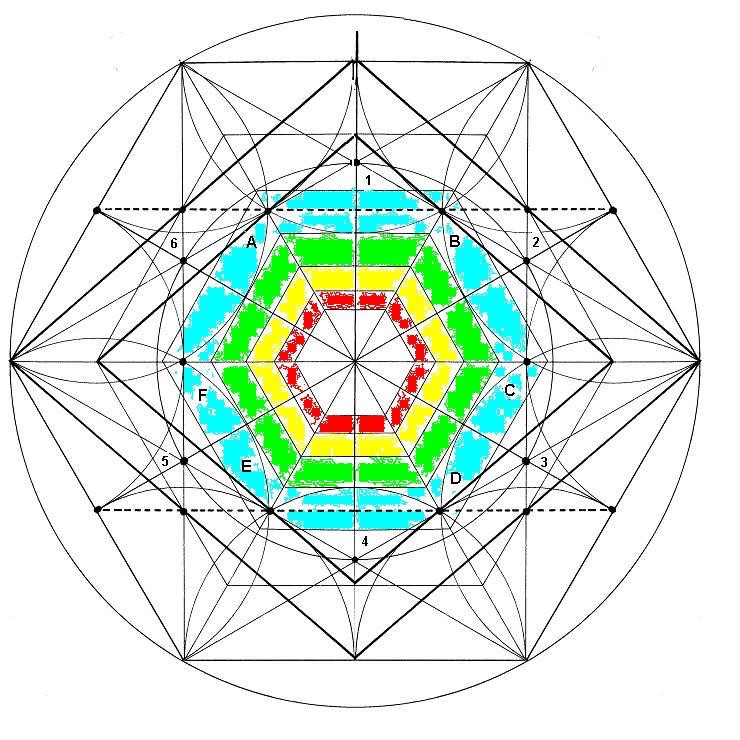
Dibujo
El color, intenta dar una idea de profundidad. A lo lejos, se ve el hexágono rojo, dentro del cual se puede dibujar un Rombo pequeño. A partir de aquí, por un crecimiento progresivo, se van desarrollando Rombos cada vez mayores, donde el más grande, abarca las informaciones de los más pequeños.
Los puntos medios de las dimensiones
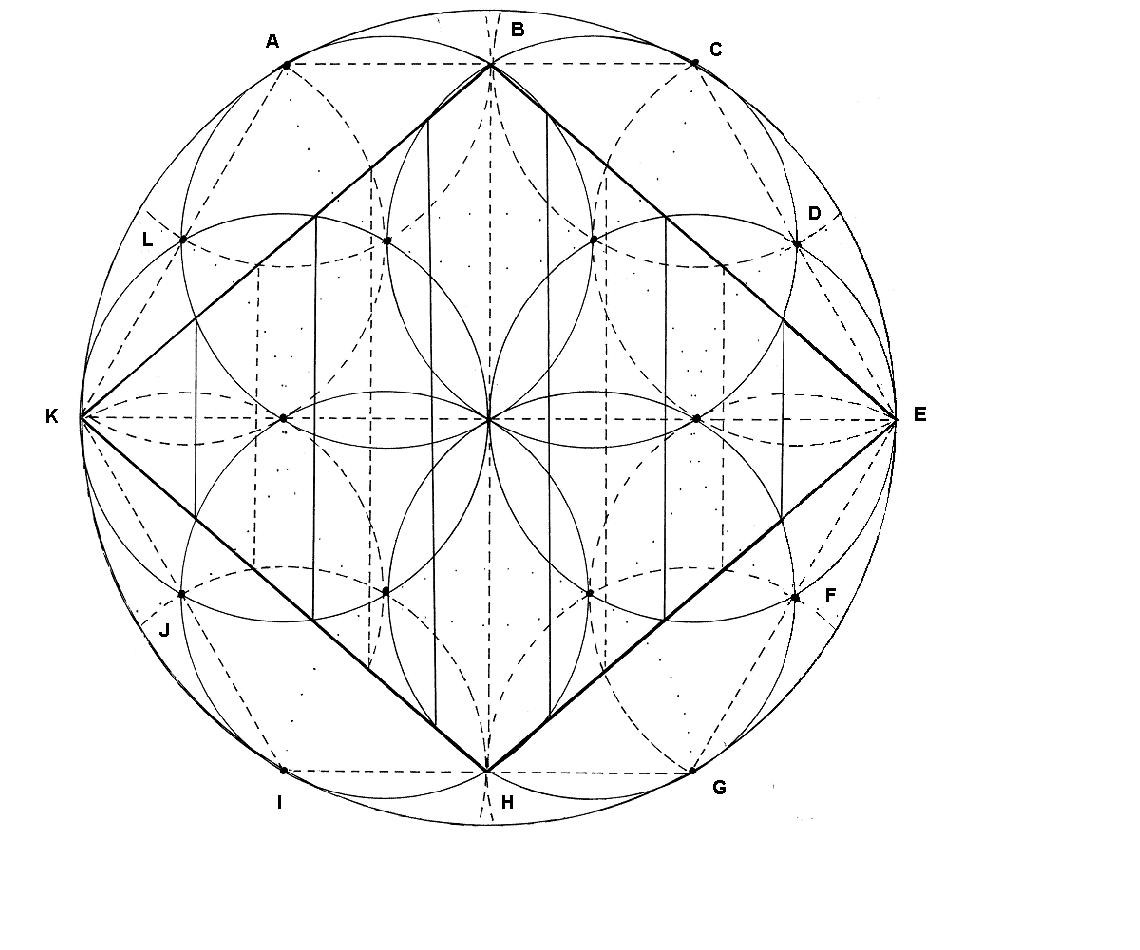
Dibujo
Desde las aristas del hexágono exterior, se marcan los puntos centrales de cada dimensión. Recordemos que los límites de cada dimensión se encontraban gracias a los focos, que están situados en las puntas de la margarita central. Es curioso observar que se puede encontrar por este sistema el punto medio de cada dimensión, a excepción de la primera y de la séptima.
Los puntos medios de las dimensiones con color
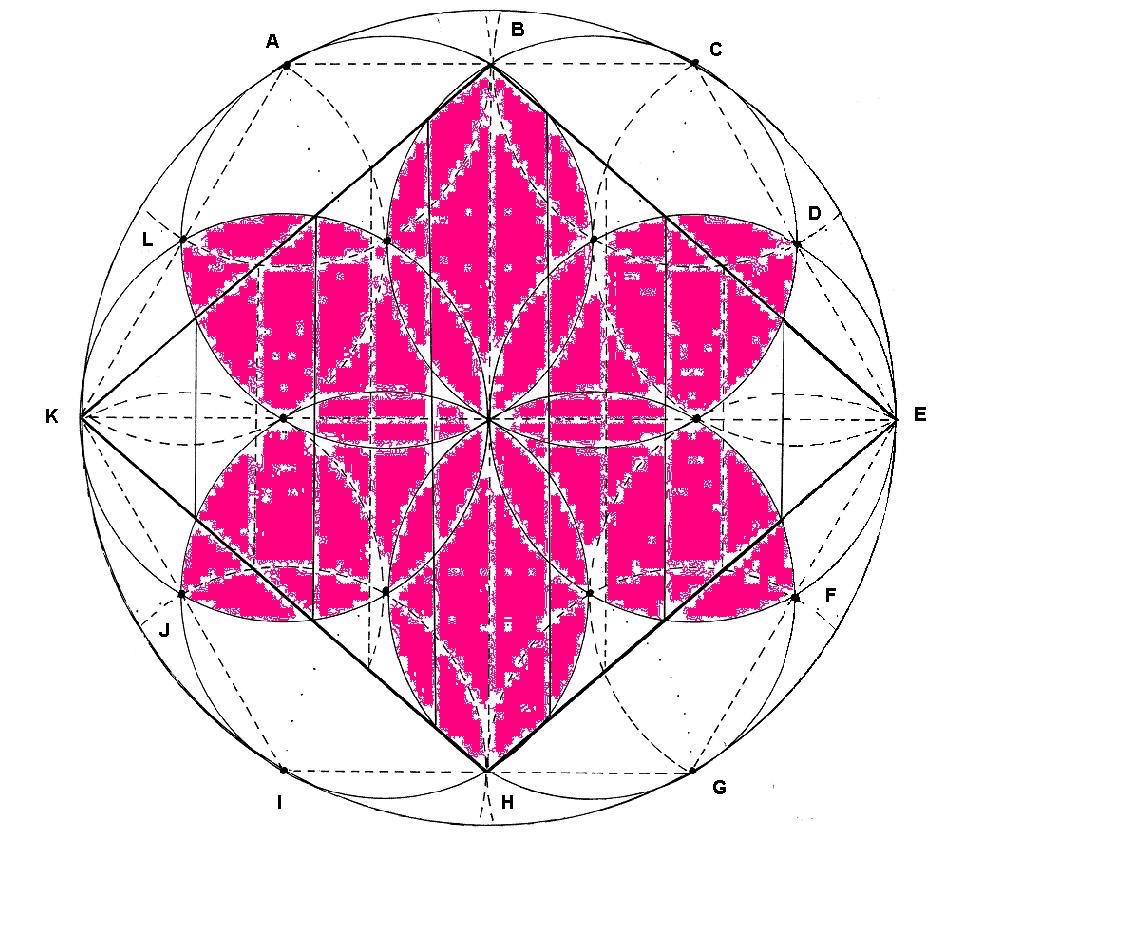
Dibujo
No lo parece, pero es la figura anterior coloreada. Las margaritas están ya muy vistas, pero esta nueva flor de seis pétalos, con cierto aire oriental, ya no tanto.
Las margaritas, nacen de la conjunción de dos pétalos consecutivos de la flor.
El timón
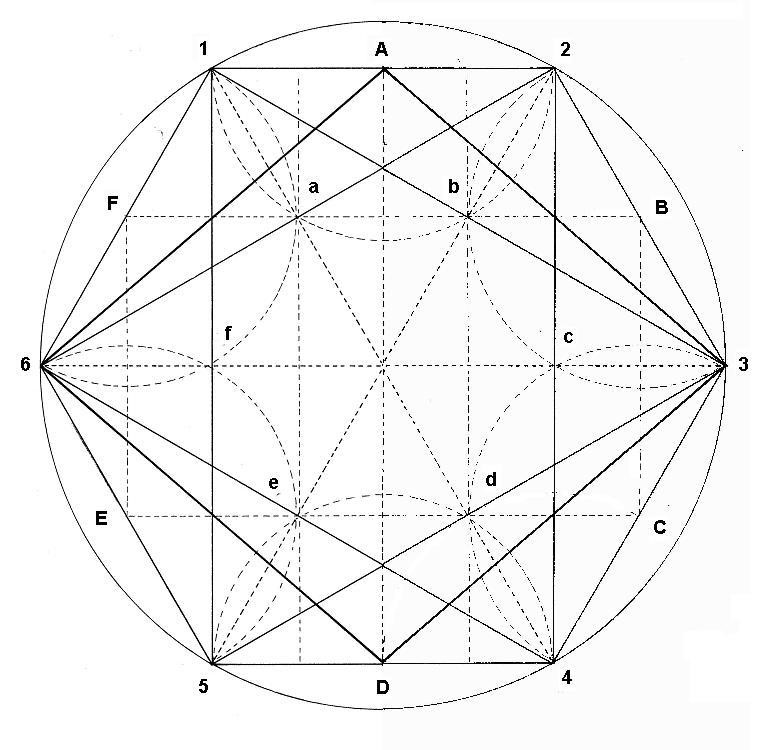
Dibujo
Tenemos por fuera el hexágono ABCDEF, con sus aristas 123456. Dentro, observamos el hexágono interior hallado desde el punto central de los lados del hexágono. Se ven también los triángulos 135 y 246, que son las dos representaciones desde arriba del Rombo tridimensional. Observamos también como el hexágono interior se puede construir desde los vértices de los triángulos equiláteros 135 y 246. En el centro aparece una figura que parece un cometa o un timón.
El timón coloreado
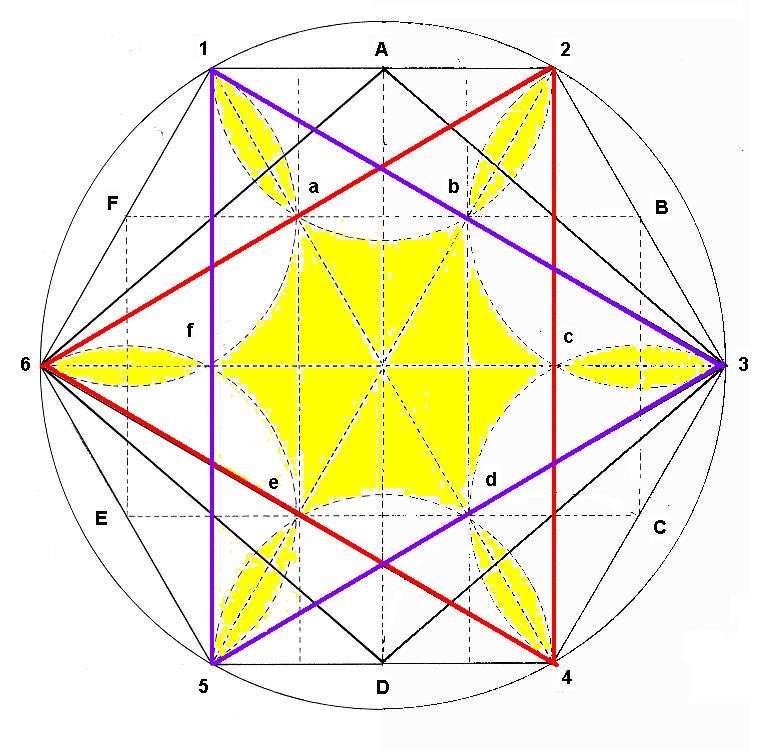
Dibujo
Es la figura anterior. Al pintarla de amarillo, se aprecia mejor la forma de timón o de cometa interior.
Los tres Rombos posibles
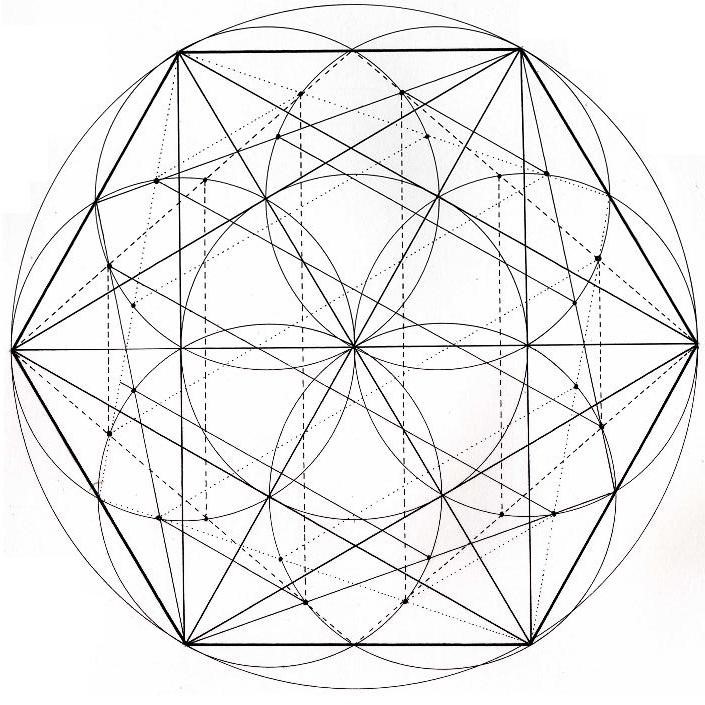
Dibujo
Dentro del hexágono, caben tres rombos posibles. Sus 6 focos son los vértices de las margaritas. Se observa como se comparten muchos puntos de límites de las dimensiones. En la figura en color, se observa con más detalle.
Los tres Rombos posibles coloreados
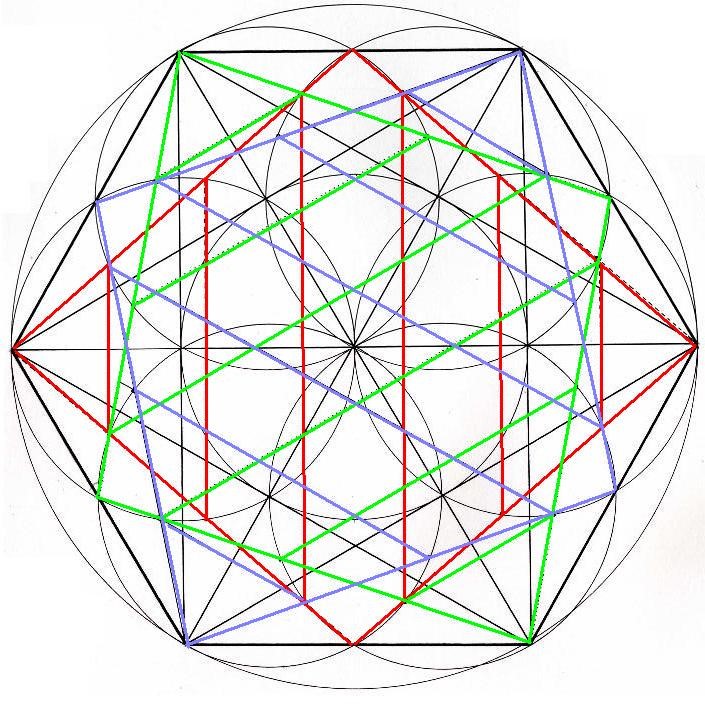
Dibujo
En rojo, verde y azul, los tres Rombos posibles. Si lo observamos con detenimiento, veremos que algunas líneas que marcan las dimensiones de un Rombo, están uniendo líneas de dimensiones de los otros dos Rombos. Los tres Rombos parece que están interconectados y se mantienen.
Si miramos bien, también aparecerá la flor oriental de 6 pétalos. Cada uno de los pétalos, acaba en la 4ª D.
El dibujo final
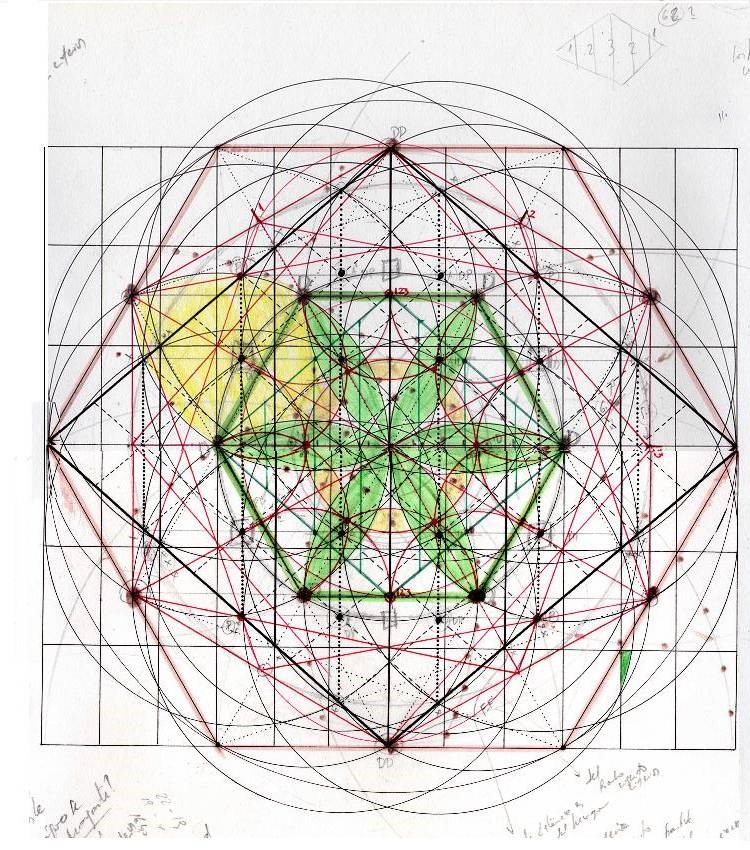
Dibujo
Este mismo, podría haber sido ser el último de la serie. Supongo que no lo pasé “a limpio”. Ahora lo miro y pienso cómo era posible que entendiera algo dentro de ese maremágnum de líneas y figuras. En este momento, me cuesta seguirlas, pero entonces no. Mientras tuve la necesidad de dibujar, lo hice con placer, pero cuando gracias a la primera serie de dibujos, conocimos los datos de la dimensión menor, el interés por hacer más series de dibujos desapareció casi por completo. No había un motivo evidente para seguir dibujando ni publicando y allí se quedaron estos dibujos, esperando su turno. Bueno, ahora, por fin, les ha llegado su hora. Aquí están.
En esta fase final de los dibujos, empecé también a buscar datos acerca del número Fi dentro del Rombo y de allí surgieron toda una serie de cálculos relativos a esta razón matemática. Pero este nuevo tema, el que hace referencia a la razón Phi, lo dejaremos para otra ocasión.