18-19 (1ª parte)

Hace unos 6 años estaba muy interesado en ese pequeño espacio situado en tierra de nadie, entre el 18 y el 19. De hecho, siempre me llamó la atención, porque nunca he entendido completamente un número así: 18-19. Así que un día pensé que la mejor manera de intentar rellenarlo de lógica era coger un compás, un juego de escuadras, un lápiz y una goma de borrar (esto sobre todo es muy importante).

Así que empecé a dibujar sin ninguna directriz y al cabo de poco tiempo, empezaron a surgir figuras y más figuras que parecían querer hablar. La primera que hizo acto de presencia es quizá la que tiene más valor de todas. Es la que aparece en la portada del artículo. De hecho, todo el trabajo   está basado en el descubrimiento y desarrollo de esta primera figura.

Cuando al cabo de un tiempo, completé estas primeras láminas, sentí la necesidad de hacerlo saber a todos los amigos del Rombo, porque pensaba que era un descubrimiento muy interesante y que podía aportar muchos datos acerca de la fisiología del Rombo, del tamaño de sus diagonales, del origen de las dimensiones, de la relación del rombo físico con el de los planos de conciencia y un largo etcétera.

Aparte de todo esto, me quedé maravillado por la belleza de las formas geométricas, de su armonía y de la relación entre la circunferencia, el hexágono, el rectángulo y el Rombo, figuras todas ellas que aparecían interrelacionadas y dependientes. Todo era muy bonito, demasiado hermoso para que fuera falso. El resultado del trabajo era que, aparentemente y de una forma lamentable, los dibujos, podían no ser considerados como pertenecientes al rombo canónico. Este debía tener una diagonal menor entre 18 y 19. De los dibujos realizados, se desprendía que existía un Rombo, cuya dimensión menor, llegaba hasta los 19’05 cm…y en principio, a pesar de su belleza, no parecía tener cabida dentro del Rombo convencional.

Este hecho tan obvio, me hizo pensar que quizá únicamente, se trataba de creaciones artístico-geométricas sin demasiado valor. Pero la estética y la cantidad de informaciones que salían de las figuras, sugerían que algo no andaba bien con el 18-19, y que tal vez, había algo que aclarar. El resultado del estudio aclaró con posterioridad, este hecho, y desveló la incógnita de la cifra. A partir de ese momento, todas las figuras, cobraron más valor, pero no nos adelantemos tanto y vayamos por partes.  

ESTUDIO GEOMETRICO DE LA FIGURA

Obtención del Rombo dentro del hexágono

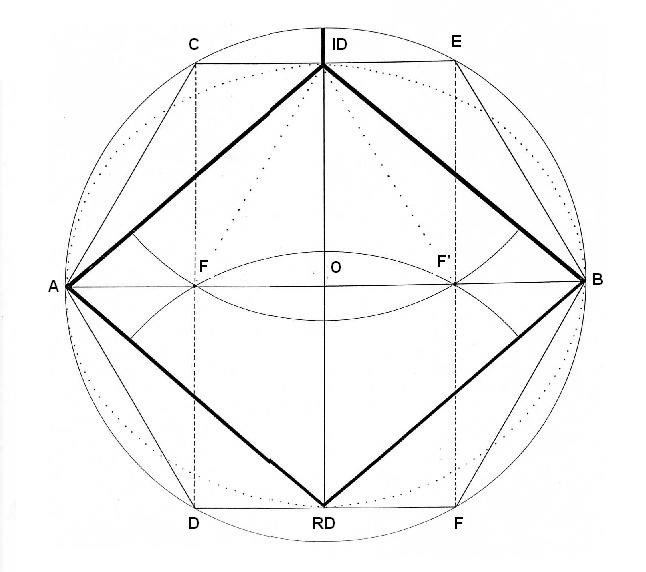
Dibujo 1

Dibujamos una circunferencia de 11 cm. de radio, (22 cm. de diámetro)

Con el mismo radio, dibujamos el hexágono. Unimos algunos puntos del hexágono y obtenemos un Rombo.

Desde ID y RD y con el mismo radio, obtenemos dos puntos de cruce en la diagonal mayor. Son los puntos F y F. (Focos de la elipse)

Unimos los vértices C-D y E-F y también obtenemos los focos

Trazamos la elipse a partir de estos dos puntos con el método del jardinero.

Constatamos la aparición del triángulo (F-ID – F’)

Observamos la línea de la ID. En este dibujo, tiene una longitud determinada, que es la distancia que va desde el Rombo a hexágono exterior.

Características de los focos

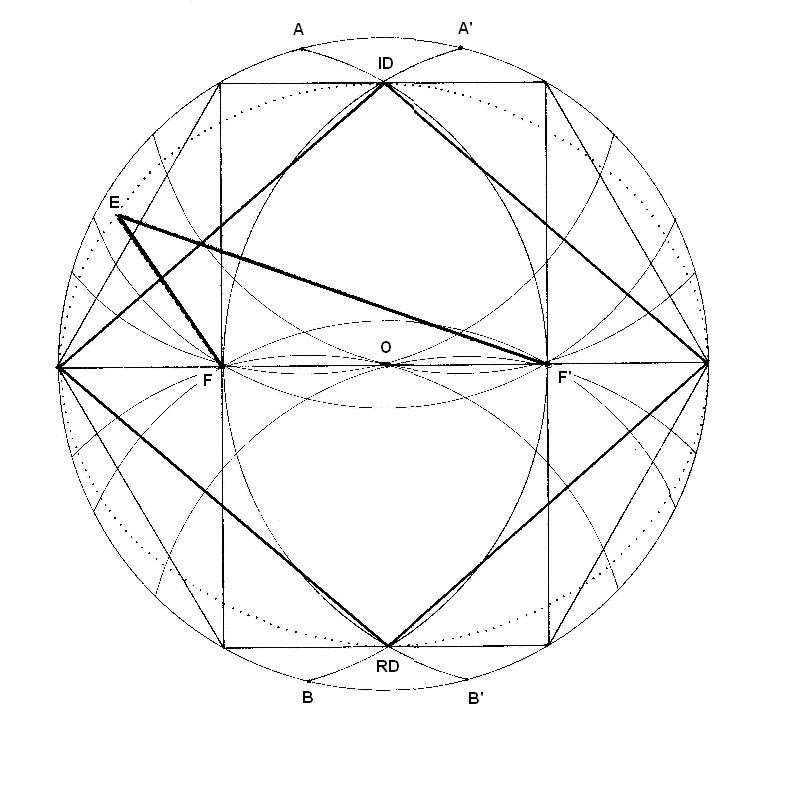
Dibujo 2

Con el radio, desde F y F, hacemos llegar curvas a la circunferencia exterior. Se crean los puntos A, A, B y B’.

Desde estos nuevos puntos y con el mismo radio, se crean semicírculos que unen focos y centro.

También se crean diversos puntos en la circunferencia exterior.

Desde los focos se dibuja la elipse. Un punto cualquiera de ella (E), está unido por un brazo corto y uno largo a los focos. Su suma es constante e igual a 22 cm.

Dibujo de los focos, excentricidad y elipse asociada

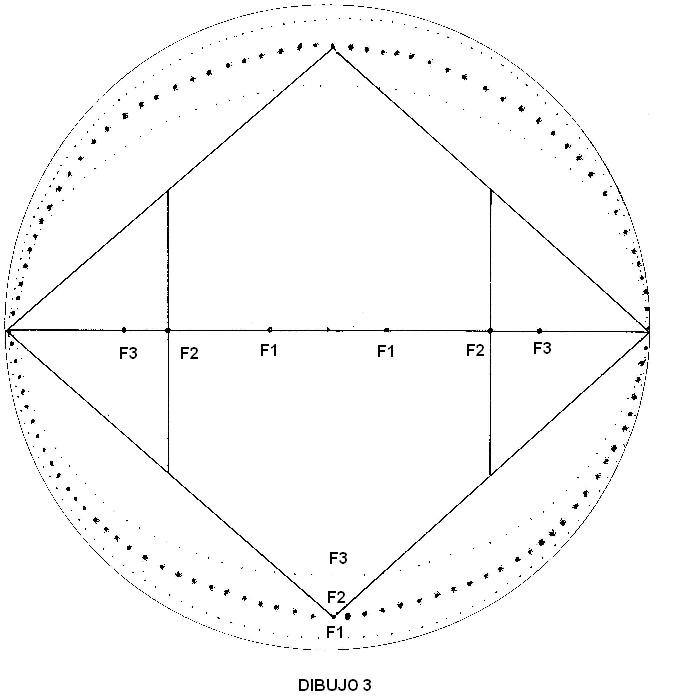
Dibujo 3

Dibujamos diversos modelos de excentricidad de elipse:

Con foco F1-F1 dibujamos la primera elipse y observamos que no llega al vértice de ID. (Elipse poco excéntrica)

Con foco F2-F2 (11 cm.), obtenemos una elipse justa, que toca exactamente los vértices de ID. Su excentricidad es de (22/11) = 0,5

Otra elipse es dibujada con foco F3-F3 y vemos que sobrepasa el límite.

(Elipse demasiado excéntrica)

Deducimos de todo esto que para cada diagonal menor, existe una elipse y un foco. Si la diagonal menor es inferior a un tamaño crítico (como veremos 19.05…), el foco se desplaza hacia los extremos y si es superior al tamaño crítico, el foco se desplaza hacia el centro. Solo existe un tamaño de la diagonal menor para el que el foco se sitúa en el centro geométrico del radio (19.05…)

Diagonal menor en el rombo inscrito en hexágono

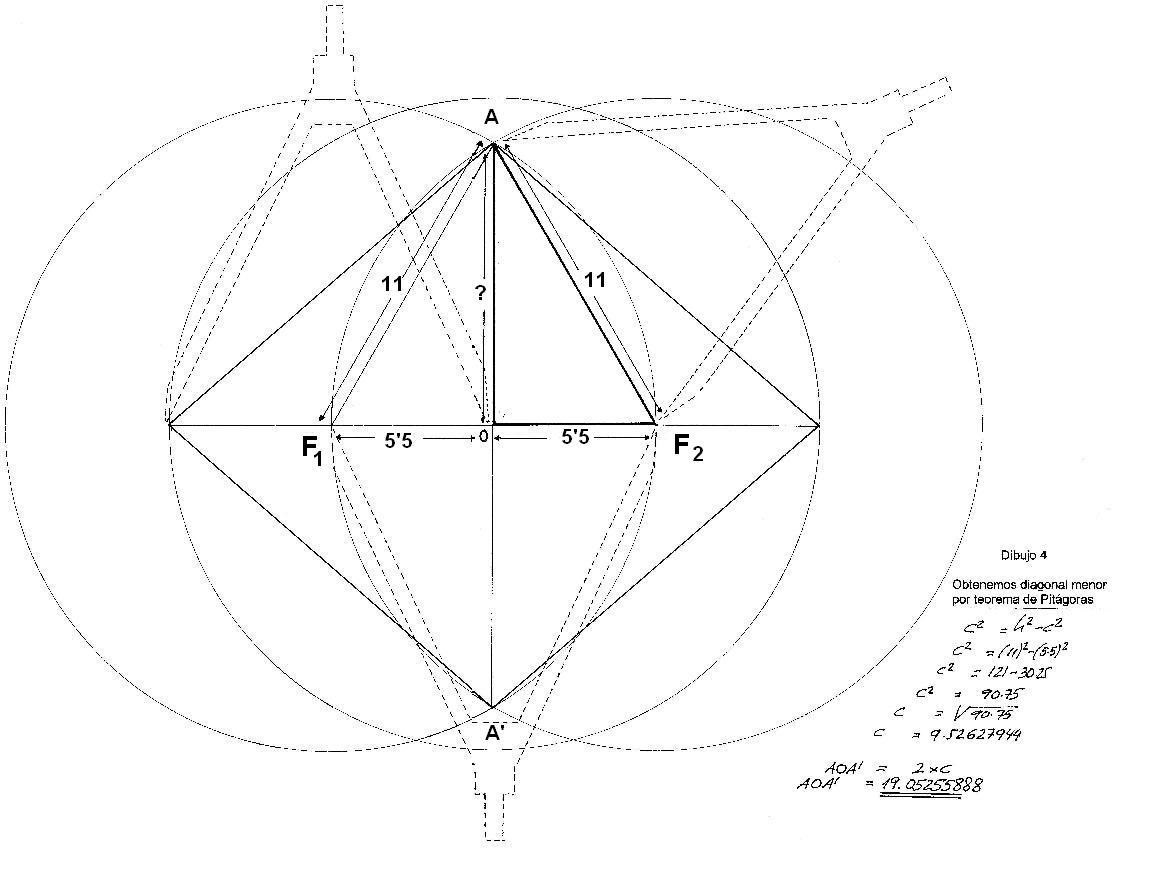
Dibujo 4

Conocemos un cateto, que es el foco. También tenemos el valor de la hipotenusa (que es el valor del radio de la circunferencia). Sólo nos falta el valor del otro cateto. Lo determinamos por la fórmula del teorema de Pitágoras

Al final de la operación, su valor es 19,05...........con este dato concreto, ya habría acabado el estudio de los dibujos que quería llevar a cabo, porque en definitiva es lo que buscaba cuando cogí el compás. Pero una vez se ha producido el descubrimiento, cuesta parar… así que seguí adelante con la serie.

El centro radial y las margaritas

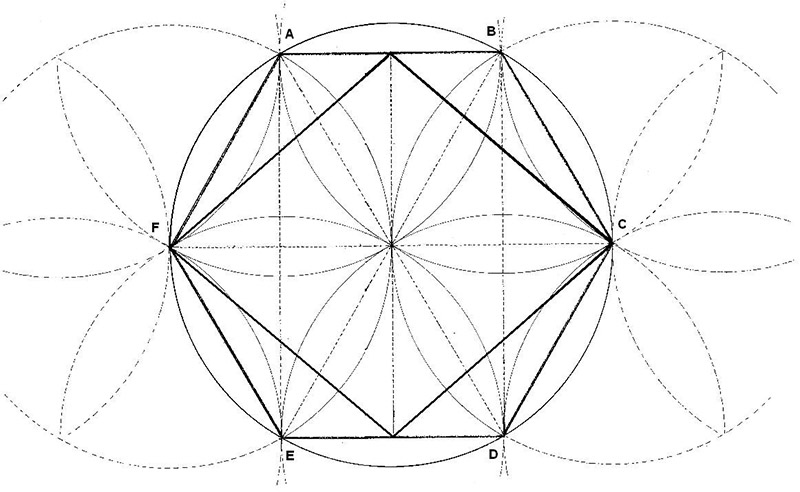
Dibujo 5

Desde los vértices del hexágono, trazamos círculos que se unen en el centro formando una margarita. Vemos también como pueden aparecer en los extremos, nuevas margaritas.

Los focos son también el centro

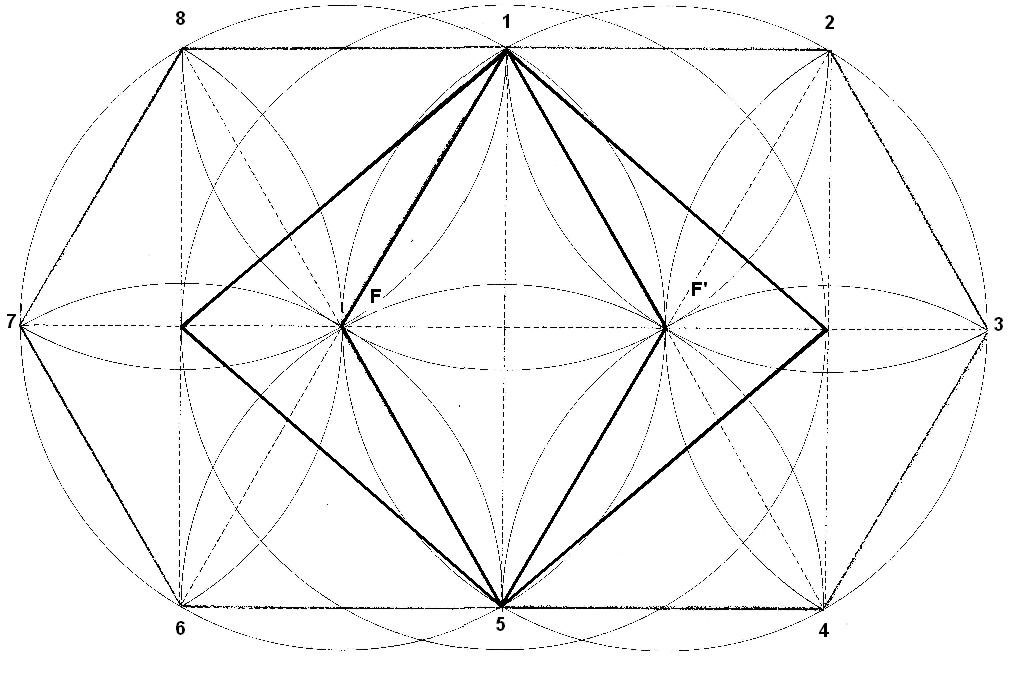
Dibujo 6

Dibujamos 2 hexágonos, uno dentro del otro. Ahora los centros de las margaritas están en los focos. El centro radial del hexágono se convierte en un foco. El foco tiene propiedades geométricas iguales a las del centro. El foco es un centro de equilibrio de la figura. De hecho, cuando estudiamos la cruz del Rombo, ya vimos que éste, se sustenta en tres puntos principales. Son el centro y los dos focos.

Las margaritas están en el centro y los focos

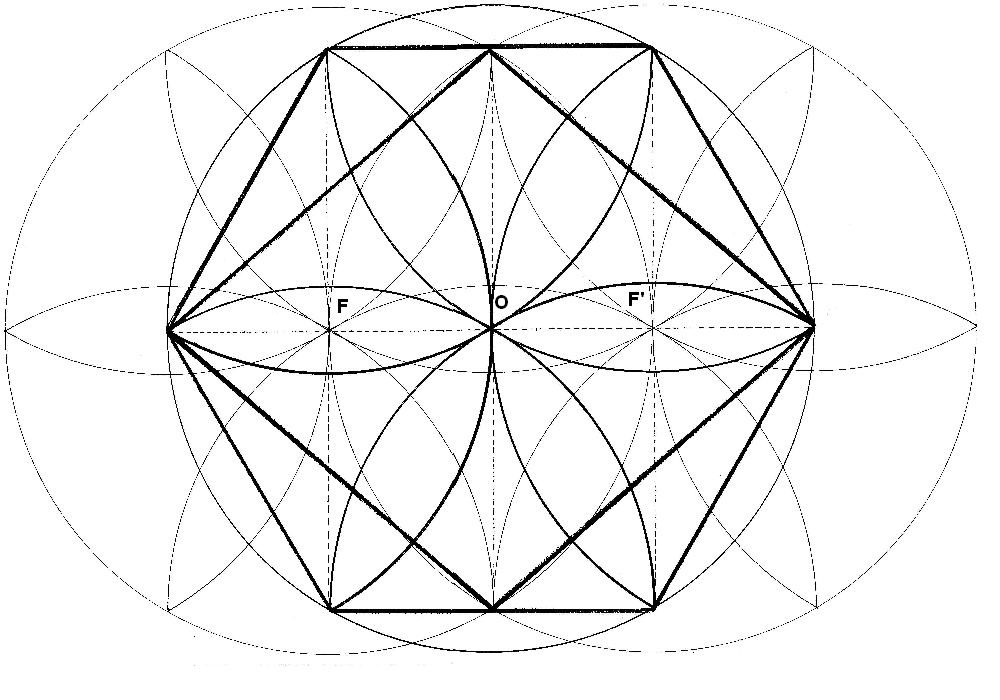
Dibujo 7

Se trata de una composición de dos los dibujos anteriores. Las margaritas están en el centro y los focos.

Los dos focos parecen ser la separación del centro hacia un lado y otro de la creación. Si el centro, se desplazara a ambos lados, se crearían los focos.

Si los focos se desplazaran hacia el centro, aparecería el centro O.

Es inevitable querer ver una movilidad desde el centro a los focos y viceversa.

Un mosaico de Rombos

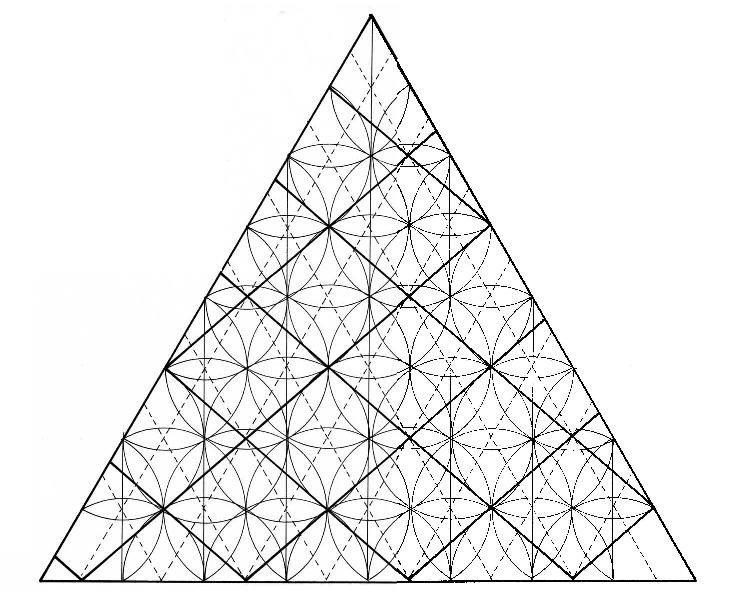
Dibujo 8

Este dibujo es un resumen de los anteriores. Tenemos una sucesión de rombos y observamos como las margaritas se distribuyen alternativamente. Aparecen unas líneas que unen focos y centros.

Mosaico de cuatro Rombos juntos y sus margaritas

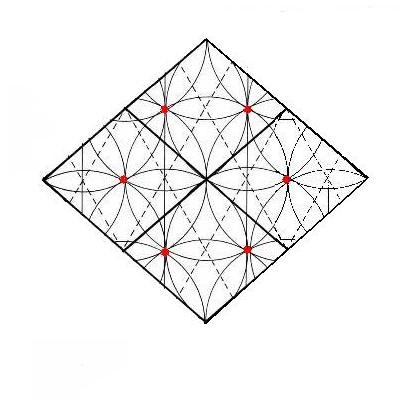
Dibujo 9

Se trata solamente de una ampliación del dibujo anterior. Hemos tomado 4 Rombos que aparecen formando un mosaico y obtenemos un Rombo mayor que los demás, con sus mismas proporciones. Si observamos los puntos centrales de las margaritas, obtendremos una figura que nos perseguirá continuamente en este ejercicio de dibujo. Se trata de un hexágono inscrito dentro del Rombo y que nos aportará datos muy curiosos.

Vemos en este dibujo una margarita interior, y cada uno de sus vértices es un punto vital para la geometría del Rombo

La Rotación del Rombo y el hexágono interior

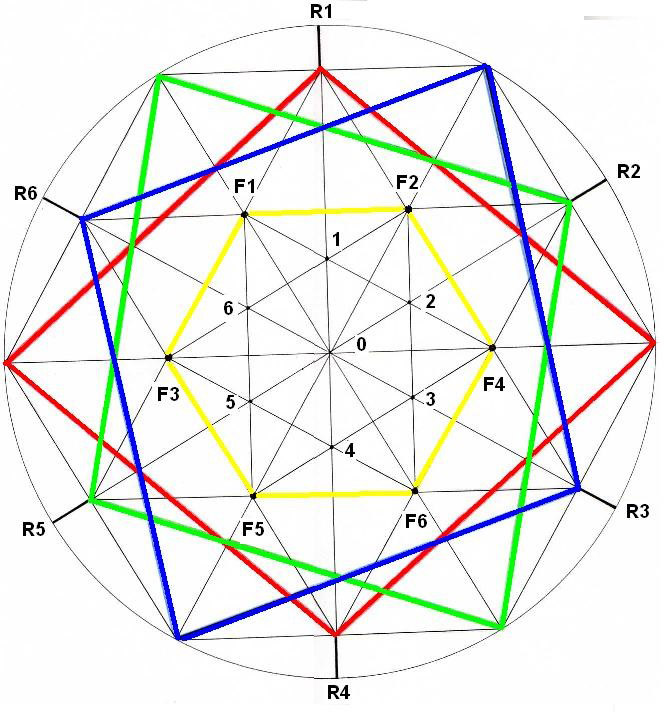
Dibujo 10

Hacemos las 6 rotaciones posibles del Rombo dentro del hexágono (R1, R2, R3, R4, R5 Y R6). Se obtienen 3 Rombos. (Rojo, verde, azul)

En cada posición del Rombo, obtenemos los dos focos ya conocidos. Al final obtenemos 6 focos que forman un hexágono interior que puede estar presente en cualquier Rombo de la rotación. Este hexágono interior, cuyo tamaño es la mitad que el exterior, está marcado por F1, F2, F3, F4, F5 Y F6 (color amarillo) y aparecerá en muchos dibujos. Este hexágono interno aparece ahora como el resultado mismo de la rotación del Rombo.

Dentro de este hexágono, a su vez, volvemos a obtener otro más pequeño,

(Marcado con los números 1-6)

El hexágono interior del Rombo

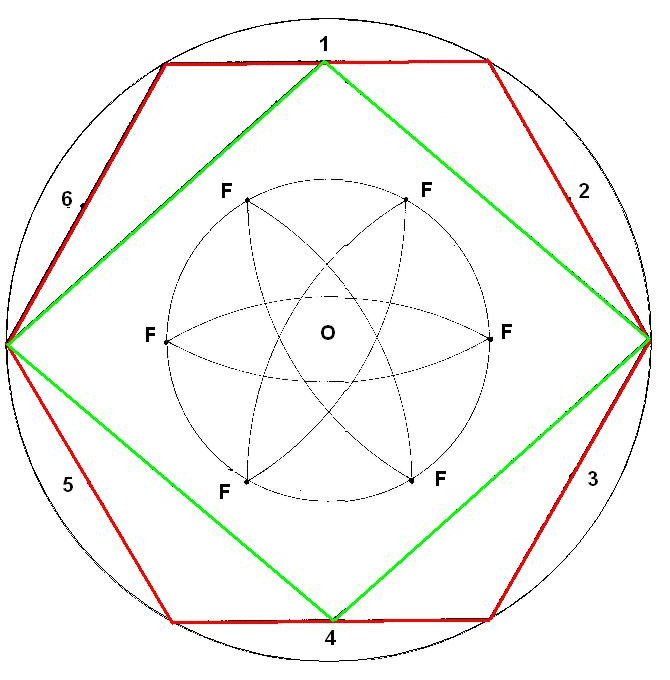
Dibujo 11

Este hexágono interior, como veremos, puede aparecer muchas veces y con distintos ejercicios de geometría. En este caso, se hace patente al hacer semicírculos desde los puntos medios de los lados del hexágono exterior.

(Desde los puntos 1, 2, 3, 4, 5, 6)

Los Focos originan las dimensiones del Rombo

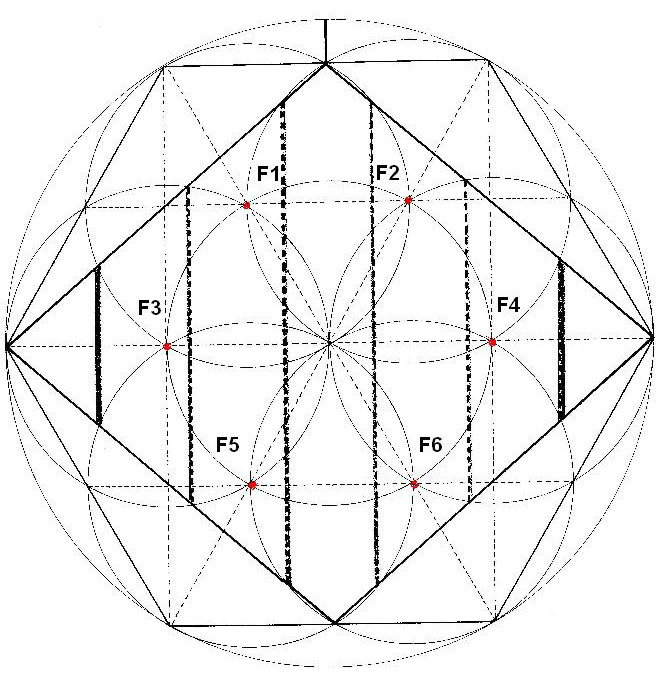
Dibujo 12

Otro modo de obtener estos 6 focos es uniendo algunos puntos del hexágono. Unimos los vértices del hexágono y nos aparecen los seis focos.

Si desde cada punto de este hexágono interior, y con radio 5´5 cm. es decir el foco, trazamos circunferencias, obtenemos puntos de corte en el Rombo.

Estas intersecciones de las circunferencias y el Rombo se dan con simetría arriba-abajo, y si las unimos, aparecen las dimensiones.

Esta figura, fue la que más me impresionó. Aparecían por fin las siete dimensiones, no por azar, sino por la misma construcción geométrica de la figura.

Las dimensiones, se muestran como un resultado inherente a la geometría interna del rombo. Los focos, que son la excentricidad del centro, construyen las dimensiones.

Las dimensiones son aproximadamente proporcionales a los focos

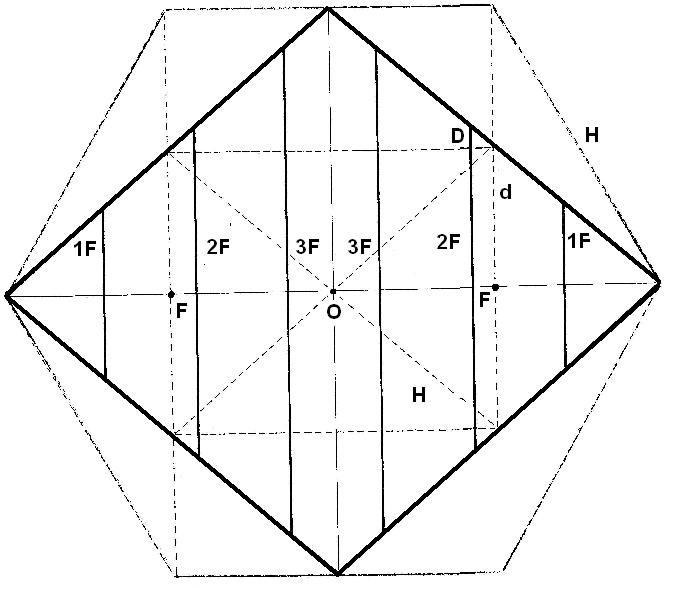
Dibujo 13

Las relaciones de los focos con las dimensiones no acaban aquí, ya que podemos ver que las distintas fronteras entre dimensiones tienen un tamaño que es aproximadamente un múltiplo del foco. La cifra no es exacta, pero este hecho, fue el que acercó a un estudio posterior, más exacto de la relación áurica de este valor. No debemos tomar el dibujo como exacto, sino como aproximado y punto de partida para cuando estudiemos el número F.

También observamos la misma longitud de las dos líneas H.

En el rectángulo central, otra figura importante, observamos sus dos lados, cuyas medidas son la mitad de las dimensiones menor (d) y mayor (D).

El rectángulo interior y la cruz horizontal

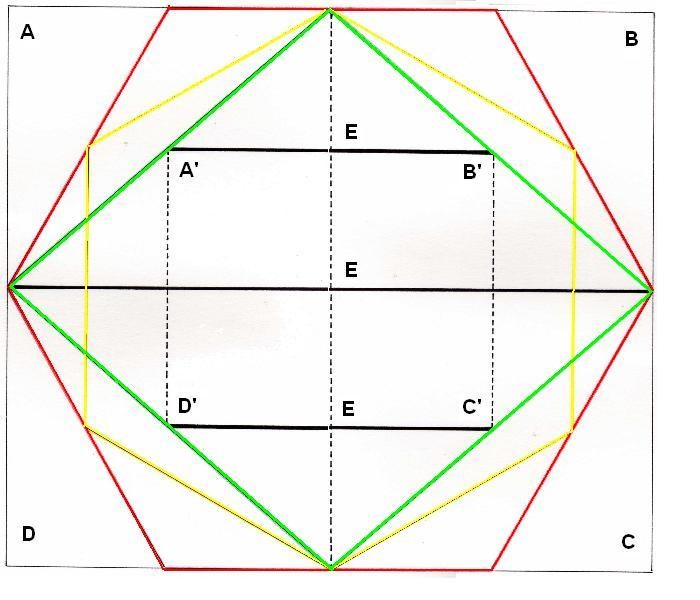
Dibujo 14

Aquí apreciamos un poco mejor el anterior dibujo y desarrollamos algunos conceptos nuevos. Tenemos por un lado el rectángulo exterior A, B, C, D, el hexágono inscrito, que a su vez tiene otro hexágono interior en rotación, el Rombo y el rectángulo interno A’, B’, C’, D’ (La mitad que el exterior)

Vemos que estos ejes horizontales señalan la unión de los dos hexágonos rotados. Esta nueva cruz guarda una relación con la ya conocida cruz vertical de los focos.  

El rectángulo interior y la cruz horizontal verticalizada

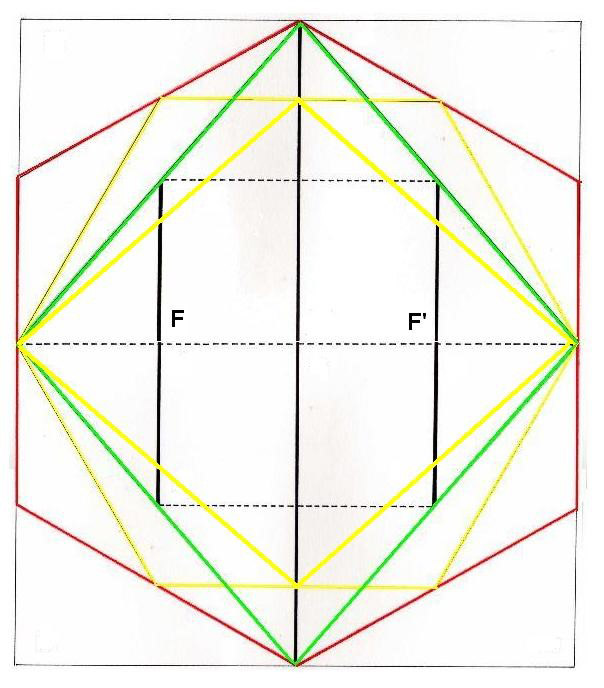
Dibujo 15

Es la misma figura anterior, pero sometida a un giro de 90º. Habíamos observado la cruz horizontal a la que mirábamos con cierto reparo, como sino la conociéramos, pero no es así. Observamos ahora, el hexágono y el Rombo amarillos inscrito en él. Vemos ahora claramente los tres brazos de la cruz. Un brazo central y dos más, situados en los focos. Estas líneas de foco que originan la cruz son lo que era antes, en el anterior Rombo (el verde) las líneas horizontales que creíamos no estaban relacionadas con nada.

El Rombo, tiene una cruz vertical, pero otra horizontal. Empezamos a ver las relaciones entre los hexágonos exteriores y los interiores.

El Rombo y las cruces

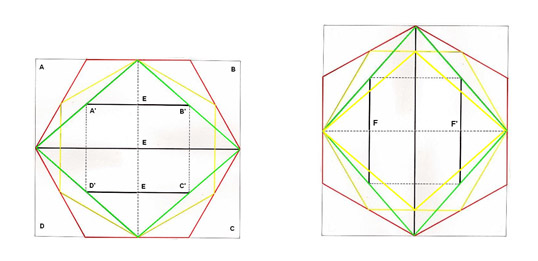
Dibujo 16

Aquí tenemos juntos a los dos dibujos. Para entenderlos, necesitamos un ligero giro del cuello y del globo ocular. Es un trabajo visual de rotación, pero nada más. El dibujo de la izquierda, más conocido para nosotros, nos presenta estas misteriosas cruces horizontales, a las que no se le daba hasta el momento, ningún valor conocido.

Si hacemos una rotación de la figura, nos aparece el Rombo de la derecha y vemos como las cruces horizontales, se transforman en las cruces verticales y conocidas del segundo Rombo.

Lo que sucede aquí es un fenómeno que veremos a menudo. Dentro de un Rombo, se inscribe otro Rombo en una rotación de 90º. Lo que era la Diagonal mayor en el Rombo exterior, se transmuta en la diagonal menor en el Rombo interior. Lo que, en un Rombo, era el eje de la 4º D, en el siguiente es el eje de planos de conciencia. Lo que en un Rombo era la cruz horizontal, en el siguiente es la cruz vertical.

El proceso se da, como imaginamos tanto en los procesos de contracción como en los de expansión.

Cada 90º, se produce una transmutación de propiedades. La verdad, es que solo de pensarlo, ya me mareo.

Teniendo en cuenta que un ciclo, son 360º, hemos de pensar que existen 4 fases de transmutación en cada situación. Son cuatro tiempos muy marcados y no creo que el hombre haya ignorado este fenómeno demasiado tiempo. De hecho, sin querer, pienso en las estaciones anuales.

Esbozos de la figura tridimensional

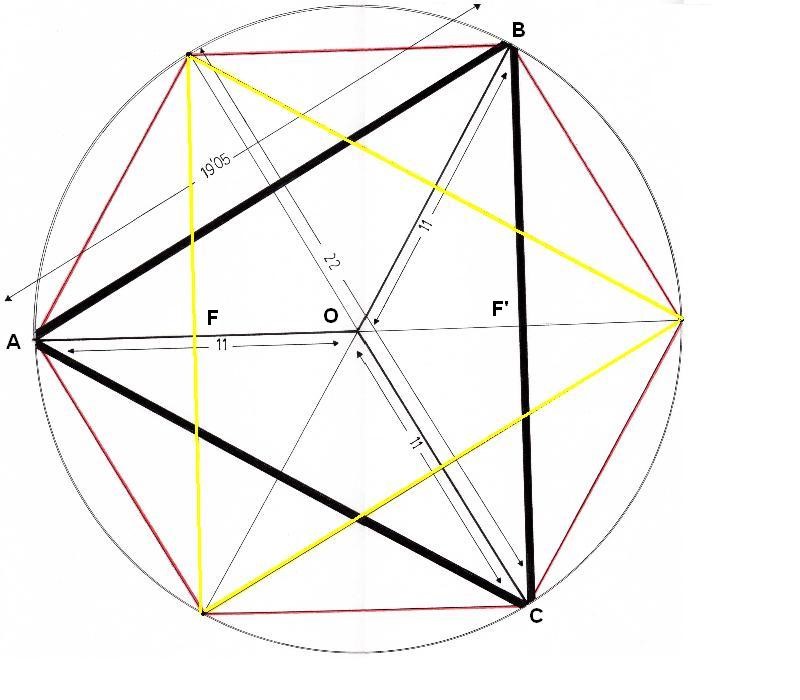
Dibujo 17

El hexágono permite construir en su interior dos triángulos equiláteros muy interesantes. Si miramos un triángulo A, B, C, veremos que uno de sus lados, formará un foco F del Rombo. El otro foco, F’, lo hará el otro triángulo.

Esta figura triangular permitirá construir la base para la figura tridimensional del Rombo. Desde el punto central del triángulo, salen tres rectas de 11 cm. que forman las aristas de la figura tridimensional. El lado del triángulo (19.05) será, visto desde arriba, la diagonal menor del Rombo tridimensional.

Desde el punto central del triángulo, salen tres rectas de 11 cm. que formarán las aristas de la figura tridimensional.

Resulta interesante ver que dentro del mismo hexágono que permite construir el Rombo bidimensional, están las claves para hacer lo propio con el Rombo tridimensional.

Las diagonales se transmutan al rotar 90º y varían según una constante

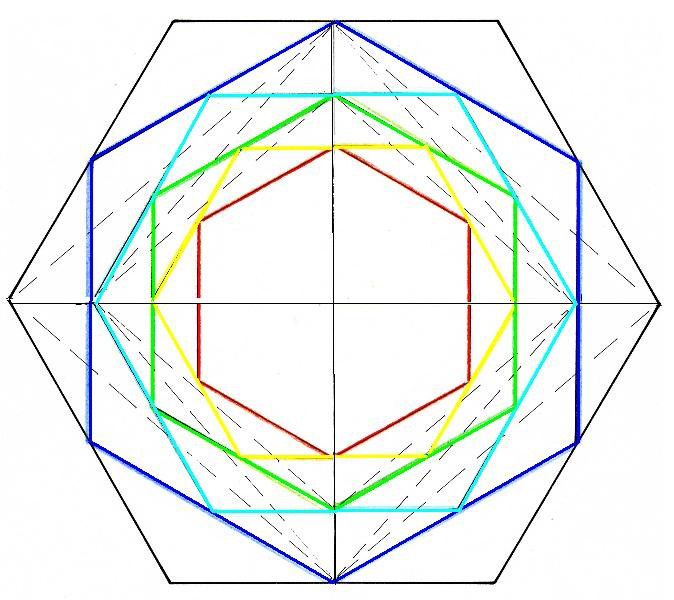
Dibujo 18

Este dibujo de hexágonos interiores pone de manifiesto una relación matemática entre la Diagonal mayor y la diagonal menor del Rombo.

Desde el primer hexágono (negro), se dibuja el Rombo. En el segundo hexágono (azul) se vuelve a dibujar. Vemos que la diagonal menor del primero es la diagonal mayor del segundo. Vemos también que el factor de crecimiento presente entre los hexágonos es igual a la misma relación que existe entre las diagonales, mayor y menor del Rombo.

Diagonal mayor = 22       Diagonal menor = 19.05255887

Factor de expansión   = 1.154700539

Factor de contracción = 0.866025403                                

                        

               2    

D = d   ____             (Factor de expansión)

               __

             √ 3                                                                                     

                 __

               √ 3

d =   D  ____             (Factor de contracción)

                

                 2

 

5 Hexágonos y 5 Rombos interiores

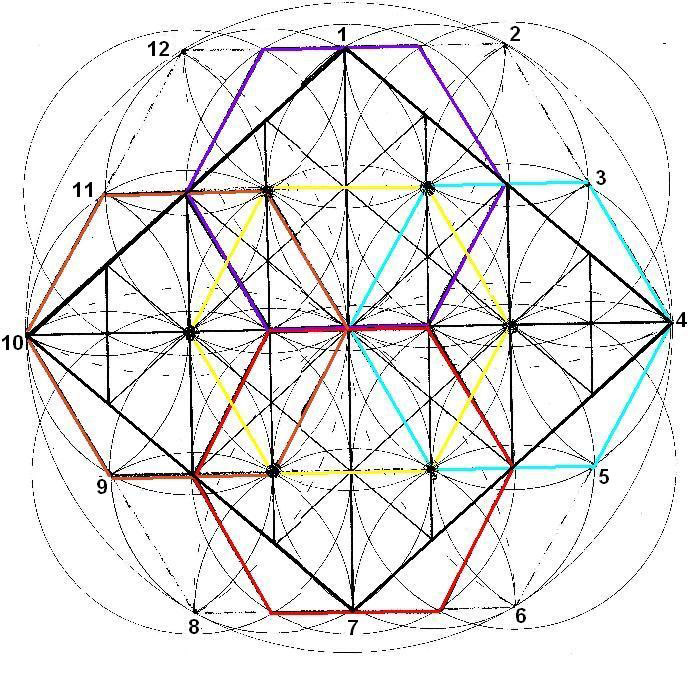
Dibujo 19

Vemos los 5 Rombos interiores con sus hexágonos correspondientes. Desde las 12 posiciones exteriores hacemos círculos. También los realizamos en el interior, desde los 6 focos conocidos y desde los 4 vértices de cada Rombo menor. Cuando las circunferencias cortan los ejes horizontales, se originan diversas líneas de foco. Se vuelven a poner en evidencia estas líneas horizontales 3 -11, 4 -10 y 5 – 9 que son las que marcan el rectángulo interior.

Las trenzas horizontales

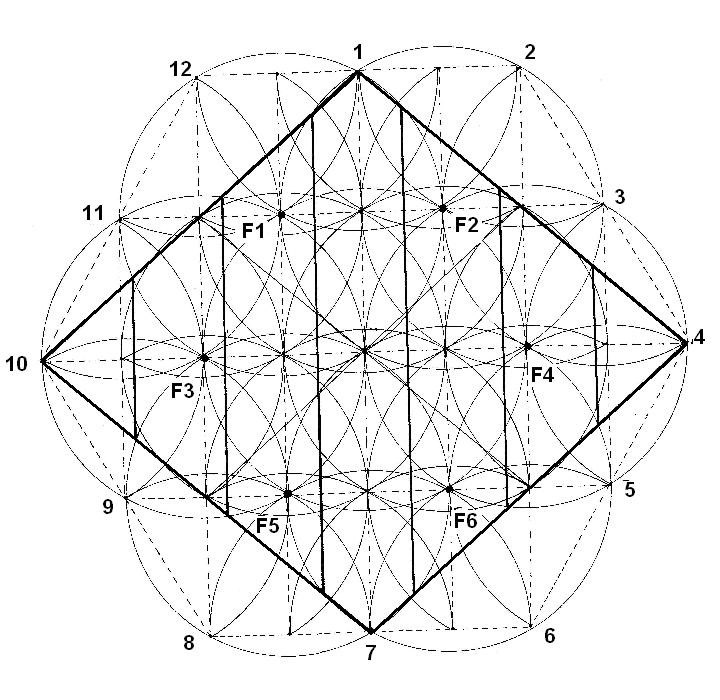
Dibujo 20

Trazamos semicírculos desde los 12 puntos exteriores, desde los 6 focos y desde los vértices de los pequeños rectángulos interiores.

Es interesante observar las tres líneas horizontales que forman estas trenzas y que nos vuelven a remarcar estos ejes horizontales del rectángulo interior.

Dentro de las trenzas, que son los caminos de la energía del foco, se ven líneas rectas y caminos semicirculares. Parece que la energía pueda correr en línea recta o siguiendo las funciones senoidales típicas de la radiación electromagnética

El rectángulo en la estructura interna

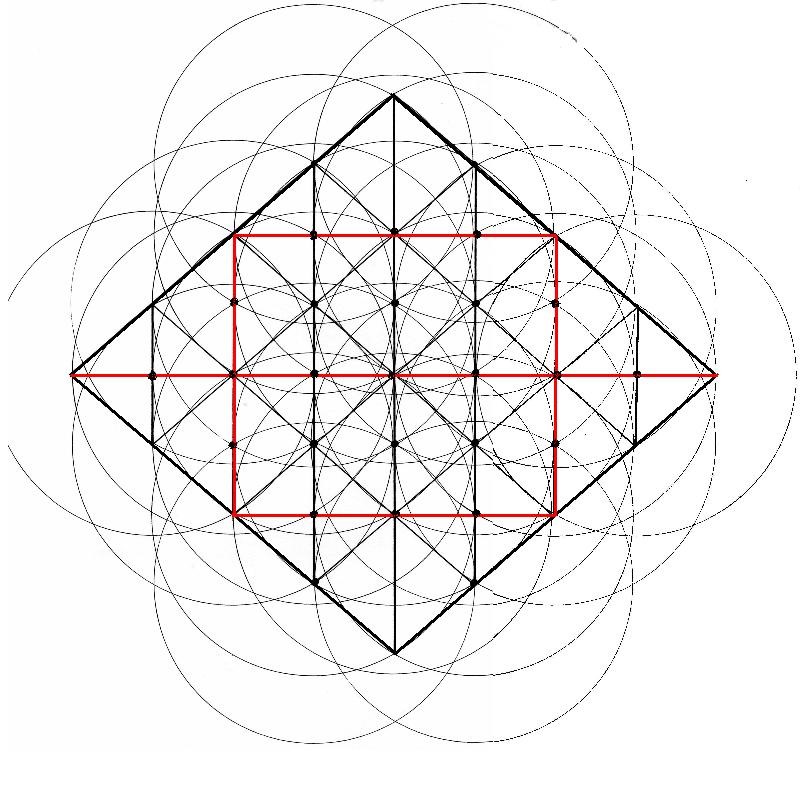
Dibujo 21

Volvemos a estudiar las líneas de foco. Debe haber un número infinito de líneas de foco y estas deben ser las principales. Los puntos marcados dentro de las líneas tocan en algún punto las líneas de foco cuando estas se unen al Rombo.

Se sigue entreviendo la estructura rectangular interna.

Hexágono, rectángulo y Rombo interior

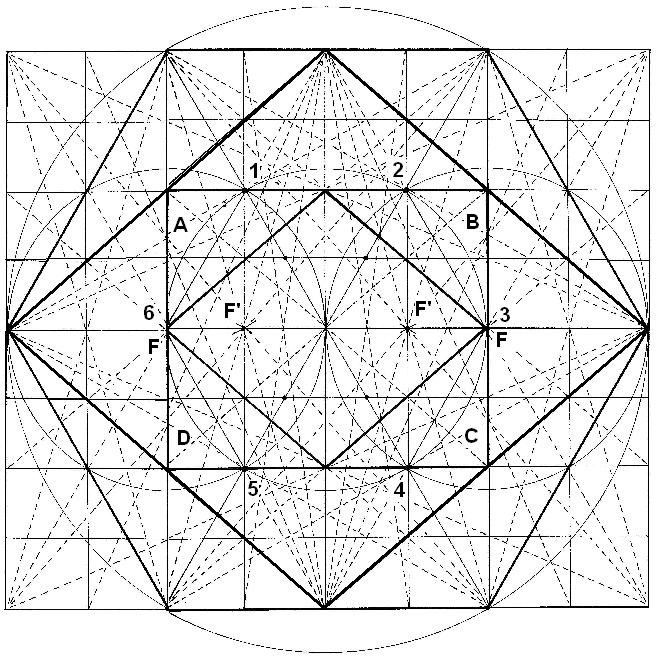
Dibujo 22

Dibujamos el rectángulo que enmarca al hexágono exterior. Vemos el rectángulo interior, con su hexágono y Rombo interior. Construimos las relaciones más importantes desde el rectángulo exterior. Notamos como aparecen en el Rombo interior todos los focos y el hexágono. Este Rombo interior es proporcional al grande, pero su tamaño es la mitad. De hecho, igual que este, que ocupa la posición central, existen 5 Rombos interiores, todos iguales.

Al acabar la serie, comprendí la maravilla de la geometría interna del Rombo. Habíamos visto la posición y el valor de los focos, el origen de las dimensiones, la relación entre las diagonales, la conversión entre el eje de la 4º D y el eje de planos de conciencia, la construcción del preciado hexágono interior, las señales para la construcción de la figura tridimensional y un tamaño concreto para la línea de la Ideación Divina, pensé que era bastante material para dar a conocer el trabajo y así lo hice. Como consecuencia de todo esto, se plantearon dudas acerca de la primera cifra 18-19, y se desveló al final un interrogante: La diagonal menor podía ir de 18 a 19.99 cm. Me sentí feliz, el esfuerzo había valido la pena, y un nuevo dato valioso, estaba allí, disponible para todo el mundo. Una duda menos.