18-19 (6ª parte)

El Rombo tridimensional puede ser considerado como la fusión de dos pirámides triangulares unidas por la base, pero también puede ser visto como el resultado de la interpenetración de dos pirámides triangulares de fuerzas opuestas que han ido la una hacia la otra y se han acoplado.

La fusión de dos triángulos

Podemos imaginar que el Rombo surge de un entremezclamiento y de una fusión de dos triángulos energéticos opuestos que van el uno hacia el otro hasta lograr fundirse y acoplarse totalmente el uno con el otro.

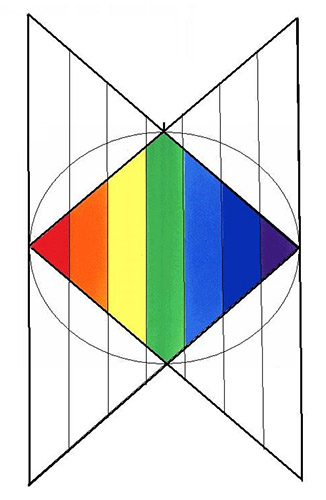
La fusión de dos triángulos

El mismo concepto de unión lo podemos ver desde una forma un poco más desarrollada en la que vemos el movimiento que se origina cuando dos pirámides triangulares, se dirigen la una hacia la otra.

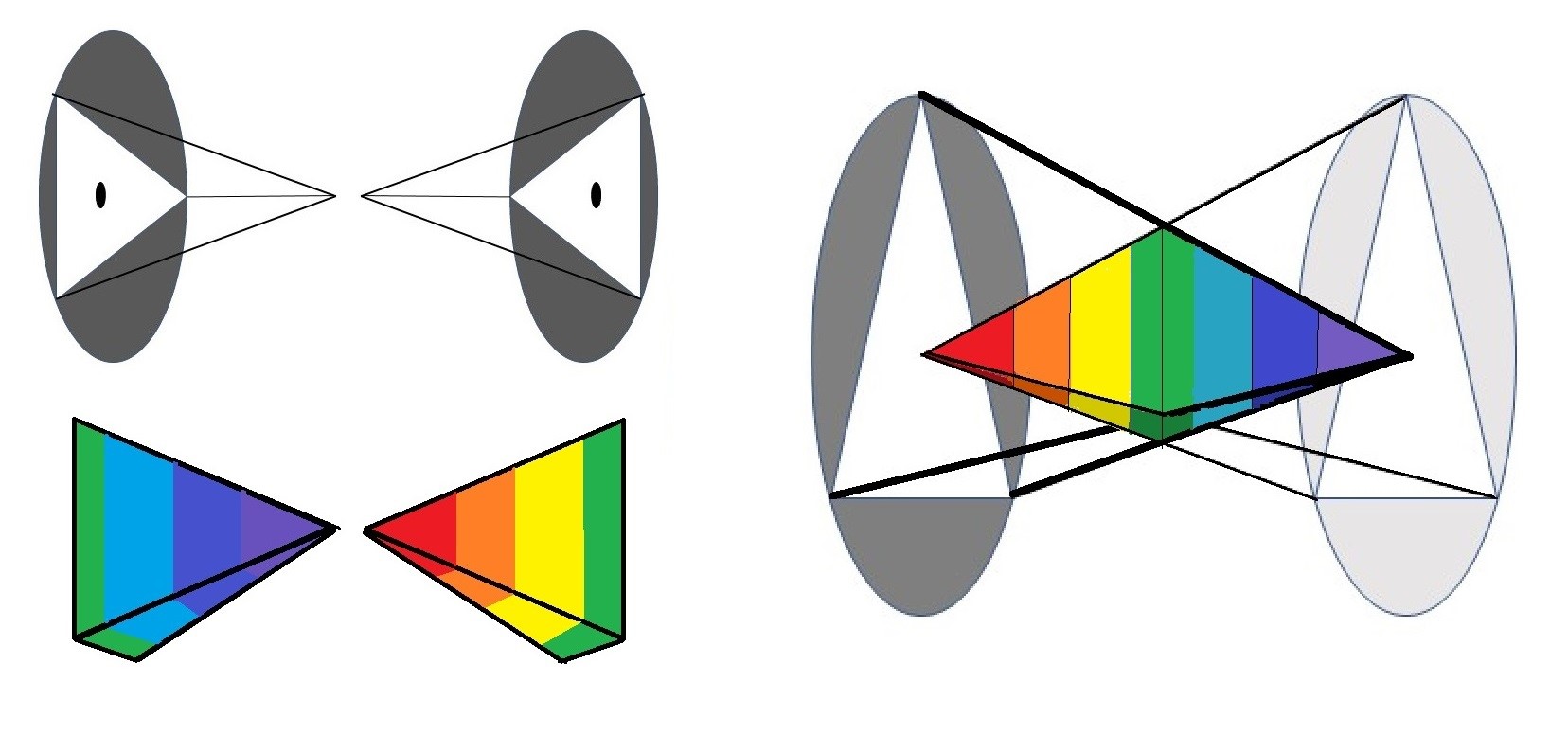
La fusión de dos triángulos en tres dimensiones

Para hacer el estudio matemático que queremos realizar, partiremos de la primera figura bidimensional, y nos vamos a centrar sólo en el triángulo que emerge desde la izquierda. A partir de aquí, empezaremos a estudiar el valor de las líneas y las áreas que se generan en este super triángulo.

LA MEDICIÓN DE LAS LÍNEAS

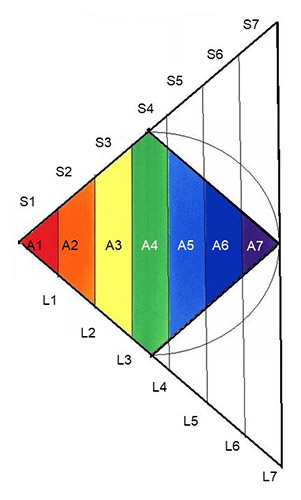
Áreas, Líneas y Superficies que aparecen en este super triángulo

Observamos en la figura un factor de crecimiento que se da en todas las líneas verticales del super triángulo. Si medimos los resultados obtenidos en la construcción geométrica de la figura, obtenemos las siguientes cifras, en las que vemos como el valor de cada línea dimensional del super triángulo, se obtiene multiplicando el número propio de la línea por 5.44, que es el valor por construcción de la línea inicial.

L1     L1 x 1 ≅    5.44

L2     L1 x 2 ≅ 10.88

L3     L1 x 3 ≅  16.33

L4     L1 x 4 ≅  21.77

L5     L1 x 5 ≅  27.2

L6     L1 x 6 ≅  32.65

L7     L1 x 7 ≅  38.08

Podemos ver que el tamaño de una línea (L) está directamente relacionado con el orden en que va apareciendo y con el valor inicial de la primera línea hallada, que es 5.44.

Vemos también que el tamaño de una línea nueva es el de la línea anterior más el valor de la primera de las líneas. El crecimiento de las líneas se da en paquetes de 5.44. Es decir, el crecimiento de las líneas va de “paquete” en “paquete” o de cuanto en cuanto.

El incremento del valor de las líneas está cuantificado

LA MEDICIÓN DE LAS SUPERFICIES

Ahora vamos a medir las superficies generadas en este super triángulo. Los valores que matemáticamente obtenemos son los siguientes:

S1  8.54 x1   = 8.54

S2 8.54 x3   = 25.62

S3  8.54 x5   = 42.7

S4  8.54 x7   = 59.78

S5 8.54 x9   = 76.86

S6  8.54 x11 = 93.94

S7  8.54 x13 = 111.02

Donde vemos que la progresión de la medida de las superficies guarda una relación con la progresión 1.3.5.7.9.11.13.

LA MEDICIÓN DE LAS ÁREAS

Hemos hablado de Líneas y Superficies del Super triángulo, pero ahora vamos a hablar de las Áreas del Rombo. De la misma manera en que el valor las líneas ínter dimensionales se va incrementando en el super triángulo según una regla matemática, la superficie de las áreas correspondientes a las dimensiones pasa por un proceso parecido de crecimiento.

Para comprobar todo ello, podemos calcular las áreas de las superficies de las dimensiones. La anchura para todos los segmentos dimensionales es la misma: 22/7= 3.1428, y la altura de las líneas inter dimensionales por construcción es el que queda reflejado en la figura.

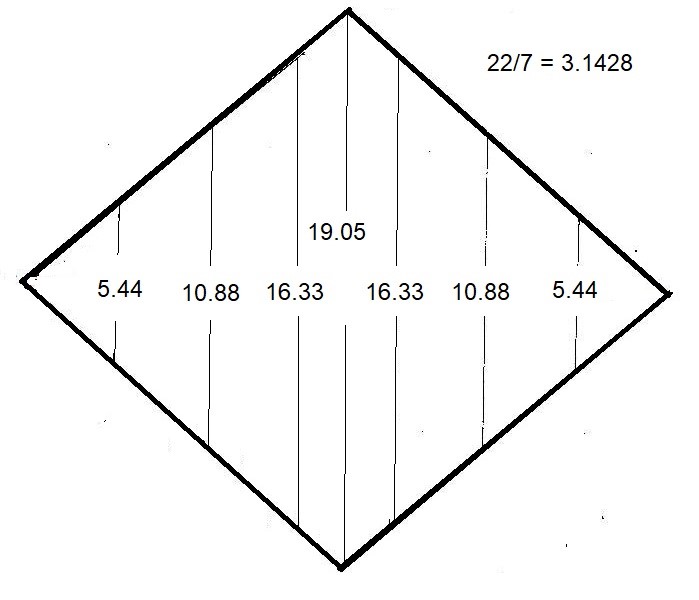
Figura del Rombo con medidas de las líneas

Vemos que la progresión del crecimiento de las áreas tiene lugar hasta llegar a la parte media de la 4ªD, donde el ascenso se detiene y se invierte, haciendo que, de este modo, se rompa la progresión que se había observado en las dimensiones previas. Con estos datos en la mano, vamos a calcular las áreas de todas las dimensiones.

Área 1ª dimensión: B x h =   5.44 x 3.14   =    8.54 cm²
                                      2                  2

Área 7ª dimensión: B x h =   5.44 x 3.14   =    8.54 cm²
                                      2                  2

El área de la 1º y 7º dimensión

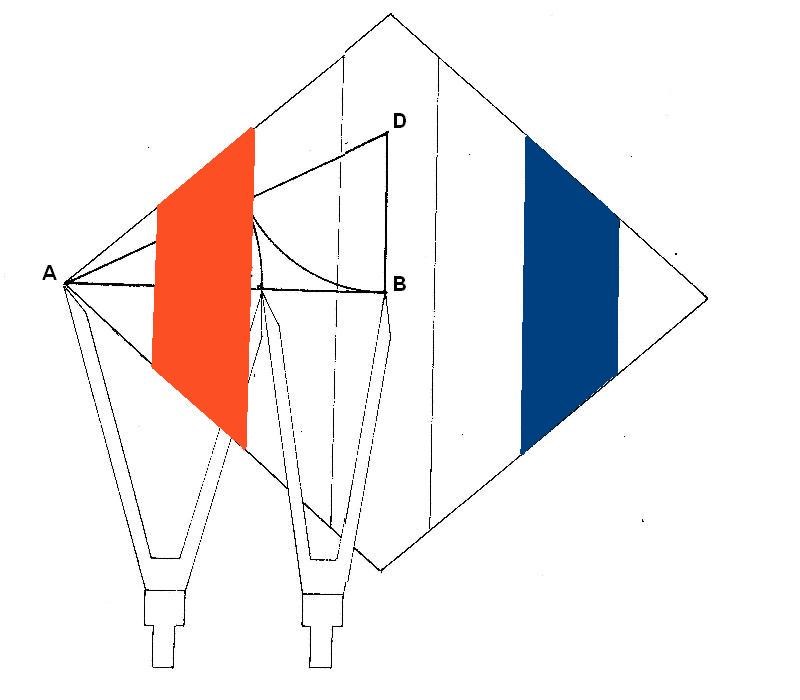
Y ahora vamos a calcular utilizando el mismo procedimiento matemático el área de la 2ª y 6ª dimensión:

Área 2ªdimensión: B + b x h = 10.88 + 5.44 x 3.14 =    25.62 cm²
                                     2                         2

Área 6ª dimensión: B + b  x h = 10.88 + 5.44 x 3.14 =    25.62 cm²
                                     2                       2

Es decir, que en ambos casos el valor de la 2ªD y de la 6ªD, es el valor de la 1ªD multiplicado x3

El área de la 2ª y 6ª dimensión

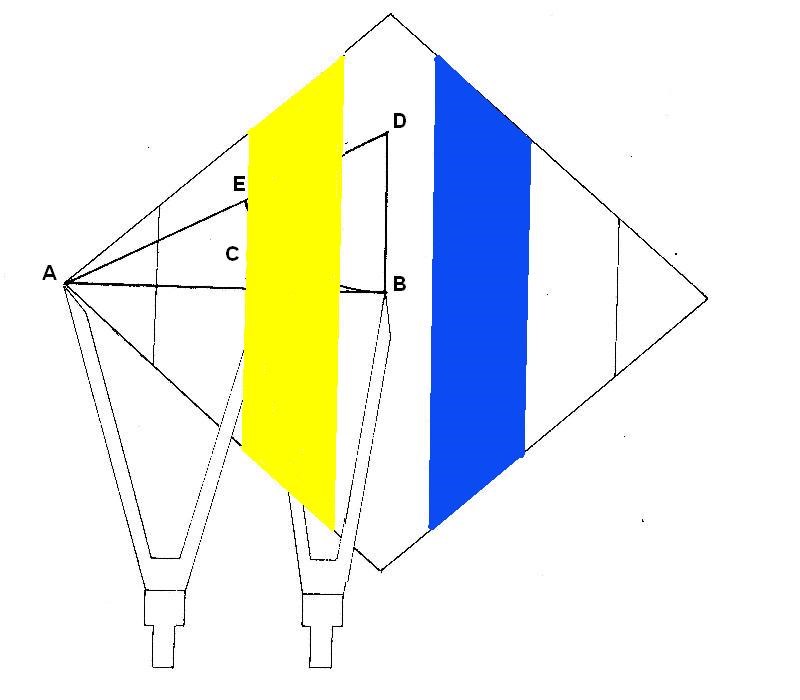
Y ahora lo mismo para las áreas de la 3ª y 5ª dimensión:

Área 3ªdimensión:   B+b x h = 16.33 + 10.88 x 3.14 =   42.71 cm²
                                      2                         2

Área 5ª dimensión:   B+b x h = 16.33 + 10.88 x 3.14 =   42.71 cm²
                                       2                       2

Es decir, el valor de la 3ªD y de la 5ªD es el valor de la 1ªD multiplicado por 5

El área de la 3ª y 5ª dimensión

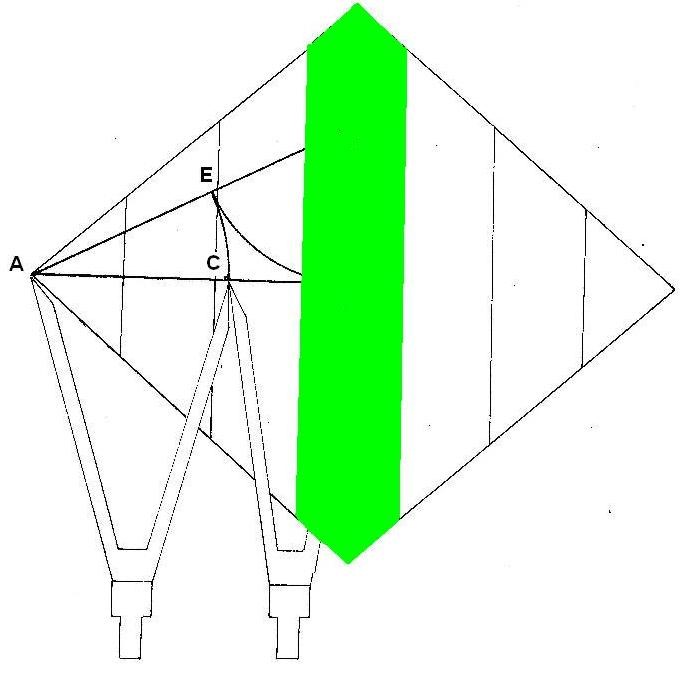
Pero en la cuarta dimensión ya no se cumple esta progresión 1,3,5,7 ya que sólo la primera parte de la 4ª dimensión es ascendente. La segunda parte es descendente. Esta área lógicamente no seguirá el mismo factor de crecimiento. Calculemos el área real de la 4ª D.

Área cuarta dimensión: B+b x h x 2 = 19.05+ 16.33 x 1.57 x 2 = 55.54 cm²
                                             2                              2

El área de la 4ª dimensión

Con estos datos, llegamos a unas conclusiones relevantes:

• Las Líneas del super triangulo siguen unas leyes cuantizadas de crecimiento = 5.44 (x1, x2, x3, x4, x5, x6, x7)

• Las áreas de las Superficies del super triángulo también siguen una fórmula cuantizada de crecimiento = 8.54 (x1, x3, x5, x7, x9, x11, x13)

• Las áreas de las dimensiones del Rombo también crecen cuantizadas = 8.54 (x1, x3, x5) hasta que llegan a la cuarta dimensión, donde esa progresión se pierde ya que una parte es ascendente y la otra es descendente. A partir de la mitad de la 4ª D, aparece la progresión de decrecimiento (x5, x3, x1)