18-19 (5ª parte)

Introducción

Dice el aforismo que una imagen vale más que mil palabras, y seguramente un objeto tridimensional al que podamos girar, mover y tocar, vale más que mil imágenes y un millón de palabras. Así que posiblemente para poder seguir este artículo con comodidad, estaría bien que pudiéramos trabajar con un Rombo tridimensional en la mano y observar todo lo que vayamos comentando. De otra manera, nos costará visualizar y comprender algunos conceptos de orden tridimensional. Este mismo modelo recortable, nos puede ayudar. Sólo hace falta imprimir, recortar y pegar.

Un Rombo tridimensional recortable

En este artículo, nos centraremos en la simetría más elemental del Rombo. No será desde luego un estudio matemático de todas las operaciones de simetría que se dan la figura, porque es un tema que, por su extensión y complejidad, se nos escapa del actual marco de interés general. Pero si que hablaremos de las características geométricas más evidentes que podemos observar sin ninguna dificultad. Hoy vamos a considerar los dos tipos básicos de simetría que existen dentro del Rombo: la simetría especular y la simetría axial.

SIMETRÍA ESPECULAR

Empecemos por describirlas: La simetría especular, es la que tiene lugar cuando una línea imaginaria divide una figura cualquiera, y lo hace en dos partes iguales, cuyos puntos simétricos son equidistantes a dicho eje. En una figura bidimensional, este tipo de simetría trabaja sobre un eje de simetría y en una forma tridimensional, esta simetría se manifiesta como un plano de simetría, que divide a la figura de tres dimensiones en dos partes iguales.

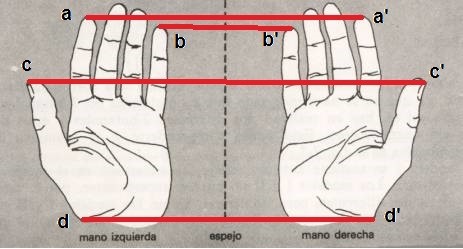
Simetria especular

La simetría especular es una aplicación matemática en la que se conservan las distancias entre los puntos iniciales y sus homólogos, pero su orientación es la inversa. Para que podamos decir que estamos frente a una simetría especular, se han de dar las siguientes condiciones:

a) La distancia de un punto y su imagen al plano de simetría, es la misma.

b) El segmento que une un punto con su imagen simétrica, es perpendicular al plano de simetría.

En la figura clásica del Rombo, observamos muy claramente los dos ejes de simetría especular: La diagonal menor y la diagonal mayor. En la diagonal menor (en rojo), observamos que los dos puntos “d“, están a la misma distancia del eje y el ángulo que forman con el eje es de 90º. Y en el eje de simetría de la diagonal mayor (en azul), observamos como los dos puntos “a” están a la misma distancia y forman también un ángulo de 90º.

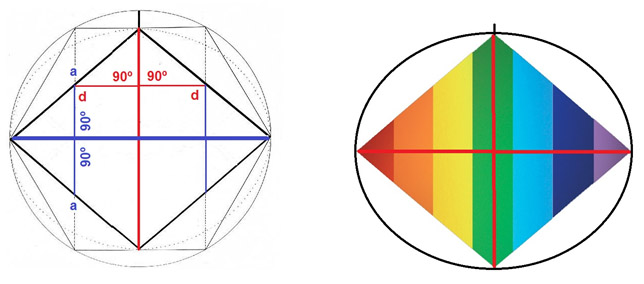
Los dos ejes principales de simetría especular en el Rombo bidimensional

LA SIMETRÍA AXIAL: EL ROMBO EN ROTACIÓN

El otro tipo de simetría que mencionamos al principio del artículo es la simetría axial (también llamada rotacional o radial). Como que el Rombo es tridimensional y está en movimiento, la lógica nos invita a estudiarlo desde el movimiento continuo que presenta.

Empezaremos por hablar de la simetría axial ya que es la que nos permitirá estudiar una parte de las características simétricas del Rombo. El eje de simetría axial es un eje tal que, al rotar alrededor de él, la figura geométrica, resulta inalterada y es perfectamente reconocible a pesar del giro que experimenta.

El número de veces que coincide la visión de la misma figura en una rotación completa se llama orden.  El Rombo tridimensional tiene una simetría axial o rotacional de orden tres ya que, en un ciclo completo, en una vuelta, la figura romboidal se ve en tres ocasiones.    

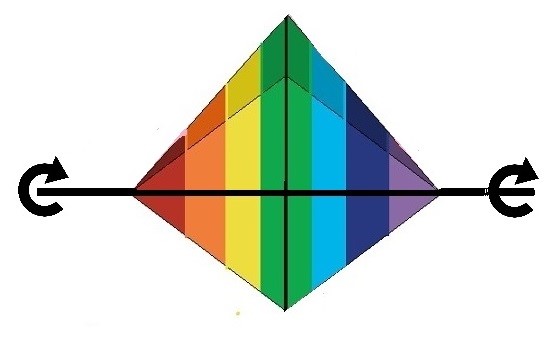
Un eje imaginario hace rotar al Rombo y aparece tres veces en un ciclo

En un ciclo completo, en una vuelta, aparecen tres Rombos, uno detrás del otro y los tres son iguales. Desaparece un Rombo y aparece el siguiente de idénticas características. Es por este motivo que decimos que el Rombo tiene una simetría axial de orden 3.

Como que, en cada cara del Rombo, tenemos dos ejes de simetría especular, en una rotación de orden tres, nos aparecerán las tres caras, por lo que tendremos 2+2+2=6 ejes de simetría especular observables en la presentación frontal del Rombo y en un ciclo completo.

Cada cara presenta 2 ejes de simetría

Cara frontal del Rombo = 6 ejes de simetría especular

Pero, si observamos con detalle la rotación de la figura a través del eje, veremos que mientras la cara 1 va descendiendo, va apareciendo por detrás la cara 2.

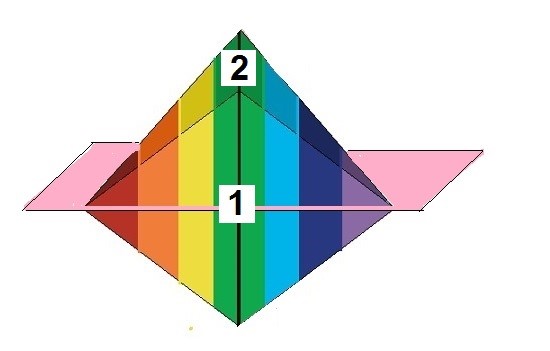
Cuando desaparece la cara 1, aparece la cara 2

Y hay un momento, en que las dos caras se han manifestado al 50%, y en ese momento, aparece otra simetría, en la que la diagonal menor es la cuarta dimensión y la diagonal mayor la forman las dos aristas superiores del Rombo.

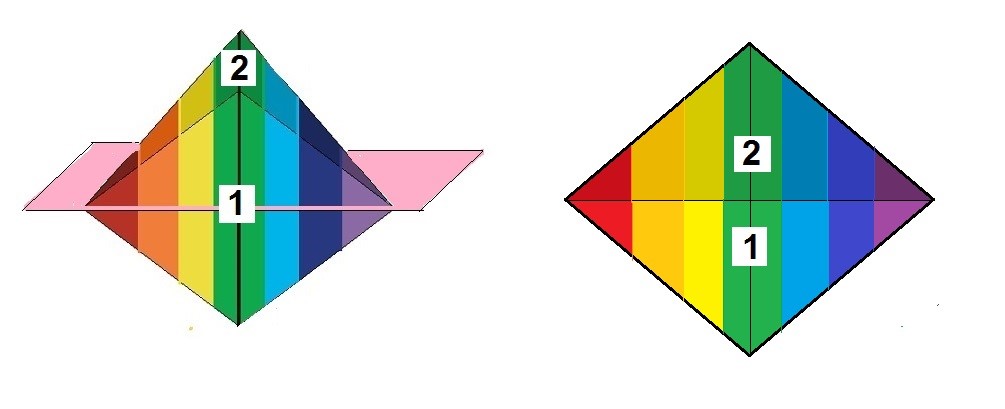
Simetría especular efímera entre la cara 1 - 2

En este instante, en el momento intermedio de transición entre una cara y la otra, aparece una simetría efímera pero real entre la cara 1 y la cara 2.

Instantes después de que aparezca esta simetría, continúa el giro de la figura y vuelve a suceder lo mismo durante la transición de la cara 2 y la cara 3 y finalmente en la transición de la cara 3 y la cara 1.

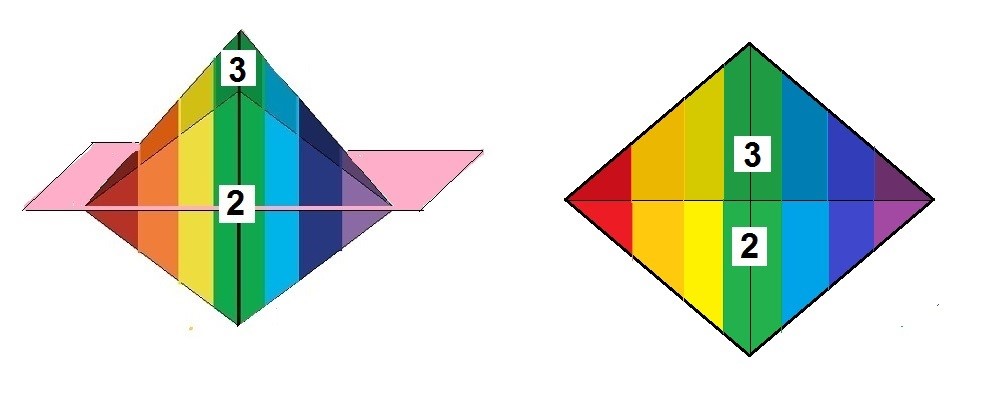
Simetría especular efímera entre cara 2 - 3

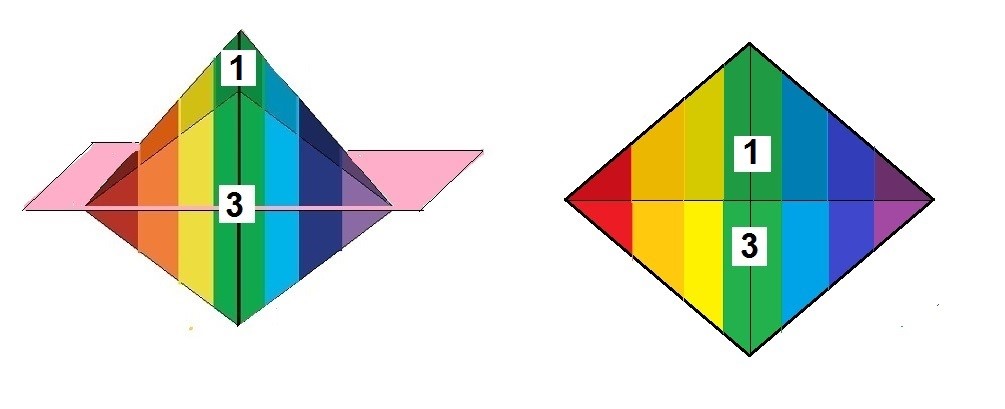
Simetría especular efímera entre cara 3 - 1

Cada simetría en la que entran en juego las dos caras presenta a su vez 2 simetrías especulares, así que hemos de entender que estas simetrías efímeras presentan 2+2+2= 6 ejes de simetría.

Son simetrías especulares apicales efímeras, y se han de considerar también dentro del grupo de las simetrías.

Cara apical del Rombo = 6 ejes de simetría especular

Podemos seguir adelante en la búsqueda de simetrías y en el dibujo siguiente, representamos al Rombo tridimensional visto desde un extremo (1ª dimensión) y en el centro, observamos a un punto blanco que representa la proyección del eje de rotación que corre por la diagonal mayor. Alrededor de este punto, se realiza la rotación de la figura.

La persona que está viendo el movimiento desde el exterior, observa como aparecen consecutivamente tres triángulos iguales.

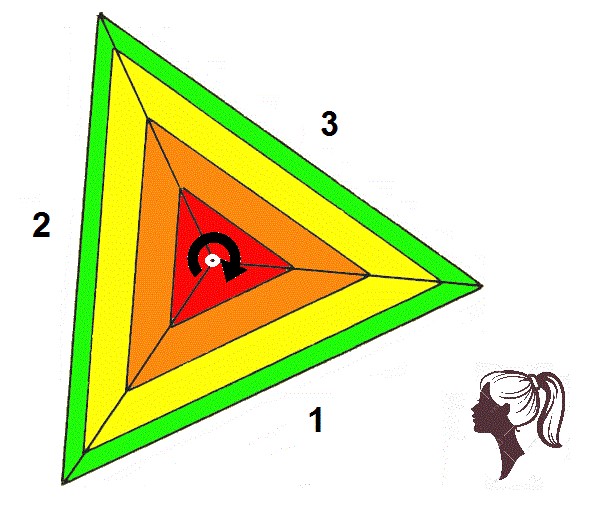
El giro del eje de la diagonal mayor es de orden 3

El eje de la diagonal mayor, que une la 1ª y la 7ª dimensión, es el único que permite realizar una rotación inalterada del Rombo vista frontal o lateralmente. Al hacer girar la figura, ésta no se altera y conserva siempre su forma. Desde la zona frontal, siempre veremos un Rombo, y desde la zona lateral siempre veremos un triángulo. En un eje axial de orden 3 al hacer rotar la figura, si la miramos frontalmente, el Rombo aparecerá en tres ocasiones hasta completar una vuelta completa y si la miramos lateralmente, el triángulo equilátero aparecerá también en tres ocasiones hasta la finalización del ciclo.

Hemos visto ya a la figura desde un punto de observación frontal y apical. Nos queda ahora observar la figura desde sus extremos. Para ello, partimos de la figura del Rombo tridimensional observada desde los extremos de la 1ª y 7ª dimensión. En estas formas, veremos cómo los ejes  a-a’, b-b’, c-c’, d-d’, e-e’, f-f ‘, también cumplen las reglas de la simetría especular.

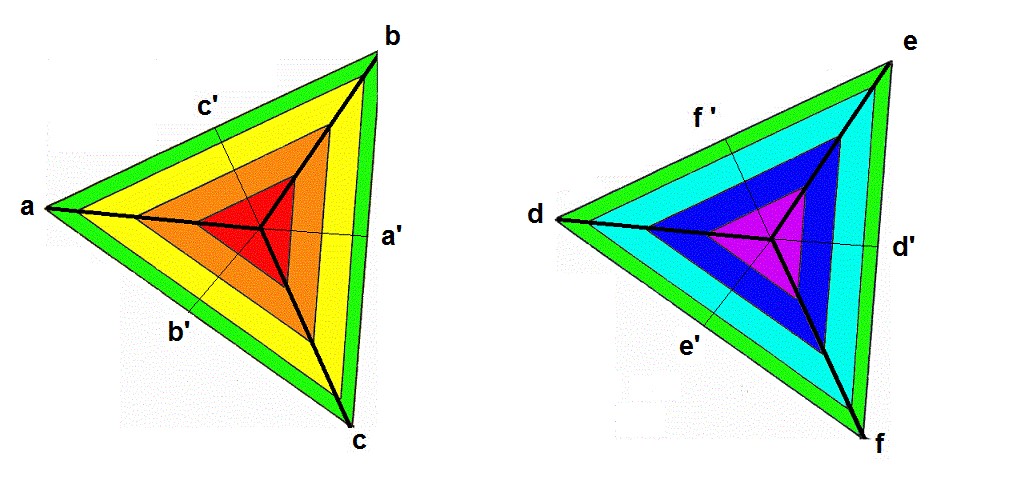
Simetría especular desde 1ª-7ª dimensión

De esta manera, en cada triangulo, observamos tres ejes de simetría, así que como tenemos dos triángulos diferentes, obtenemos 3+3=6 ejes más de simetría especular.

Cara lateral del Rombo = 6 ejes de simetría especular

Bueno, no está nada mal para empezar. Hemos descubierto 18 ejes y hemos de seguir, porque seguramente, el Rombo nos presentará algunas sorpresas más.

Cara frontal del Rombo   = 6 ejes de simetría especular Cara apical del Rombo     = 6 ejes de simetría especular Cara lateral del Rombo    = 6 ejes de simetría especular Total = 18 ejes de simetría especular

Vayamos ahora a por el otro tipo de simetría que no hemos comentado aún.

LA SIMETRÍA NO AXIAL: EL ROMBO EN ROTACIÓN

Aparte del eje axial, existe en el Rombo otro eje que provoca giros muy importantes. Este eje es de rotación no axial, y es el que produce los ciclos de alternancia polar Yin-Yang, y los ciclos compensatorios.

Estos giros tienen lugar gracias a un eje no axial, porque al girar, la figura en su rotación resulta alterada, ya que pasamos de observar un triángulo, a ver un rombo.

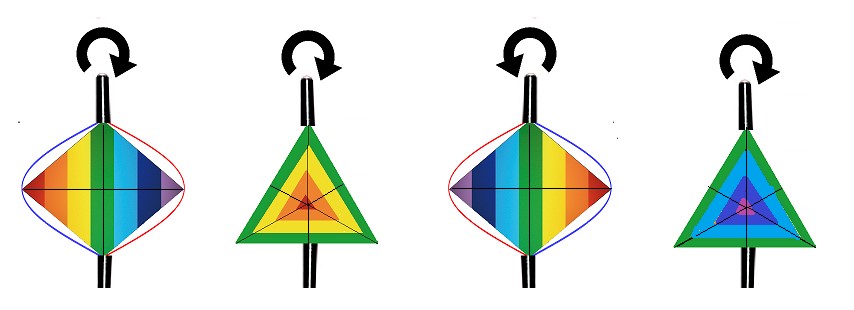
Al girar, la figura resulta alterada

Este eje rotacional no axial va desde el vértice de Ideación Divina hasta el punto central de la diagonal menor que se encuentra en el lado opuesto al vértice de Ideación Divina.

Eje de rotación no axial

En un giro completo a través de este eje, se producen cuatro imágenes simétricas (dos rombos y dos triángulos).

En este giro, aparecen 4 ejes de simetría frontales y 6 laterales, que son los mismos ejes de simetría especular que habíamos observado antes. En total, obtenemos 10 ejes ya conocidos.

Con el estudio de la simetría axial, nos aparecían 18 ejes, y con la observación del eje no axial, se aprecian sólo 10 simetrías (una parte de las anteriores), pero son las mismas simetrías.

En resumen, el eje de simetría no axial no nos aporta más ejes de simetría, pero si que nos explica de donde procede el giro que crea los ciclos de alternancia polar y de compensación.

Eje de rotación no axial = 10 ejes de simetría ya conocidos

EL PUNTO HARA

El eje de rotación no axial origina la rotación del Rombo sobre su eje, pero como existen tres ejes de rotación no axiales, se producen tres movimientos rotatorios y entre ellos tres, producen los ciclos de cambio de polaridad y de compensación.

Podemos observar que los tres ejes de rotación no axiales confluyen en el punto Hara interior que está situado en el centro geométrico de la figura.

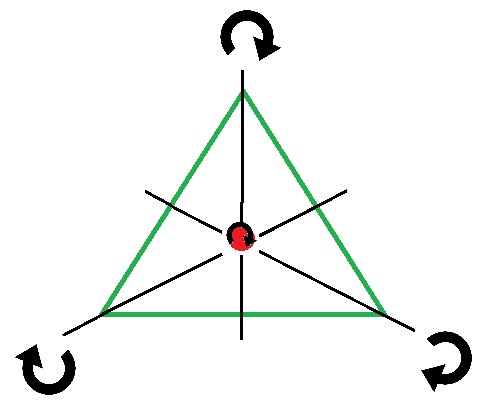
El punto Hara interior y los tres ejes de rotación no axial

Podemos considerar al punto Hara como al baricentro de la figura, ya que es un punto tal, que cualquier recta que pasa por él, divide a dicho segmento en dos partes iguales. El punto Hara, es un centro de simetría y de equilibrio del Rombo; donde confluyen los tres ejes no axiales del Rombo.

Es el centro de equilibrio y el centro de todos los movimientos de rotación y de compensación de la figura. Además, por este punto Hara, pasa también el eje de la diagonal mayor que es el que origina los ciclos recreación y retrospección.

PLANOS DE SIMETRIA

Un plano de simetría es un plano imaginario que divide a un cuerpo en dos partes iguales y que se corresponden de manera exacta. Si tomamos a la figura del Rombo, le dibujamos los ejes de simetría, y realizamos una proyección tridimensional sobre los ejes, podemos crear los planos de simetría correspondientes.

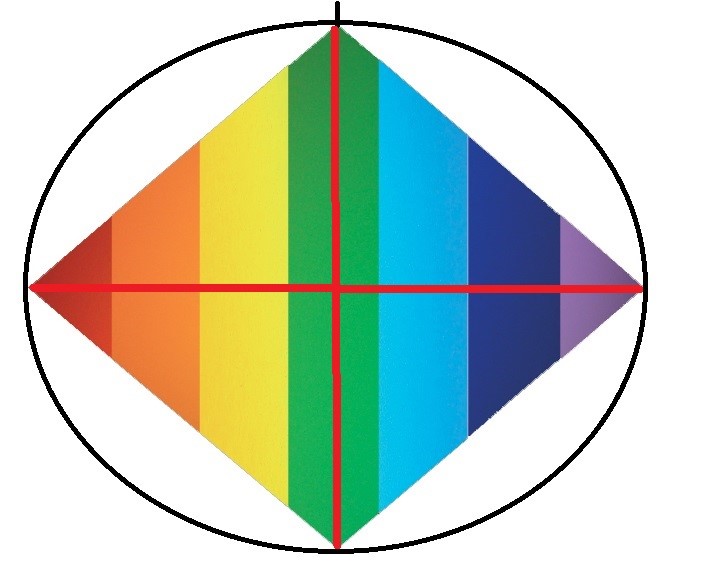
Los ejes de simetría

Al proyectar en tres dimensiones los dos ejes de simetría, que corresponden a la diagonal menor y a la mayor, obtenemos los dos planos de simetría que existen en la presentación frontal del Rombo.

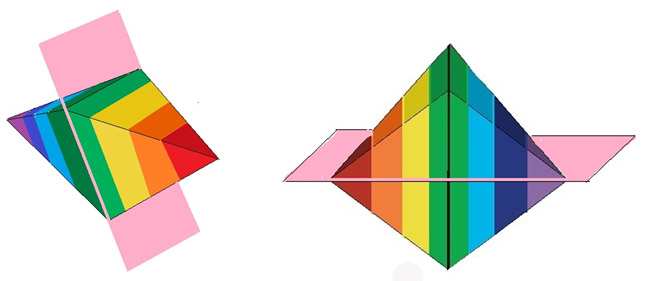
Los dos planos de simetría frontal del Rombo

En este caso, analizando la vista frontal de la figura, obtendríamos los dos planos de simetría que existen, uno perpendicular y otro horizontal, que dividirían perfectamente al Rombo en dos mitades simétricas.

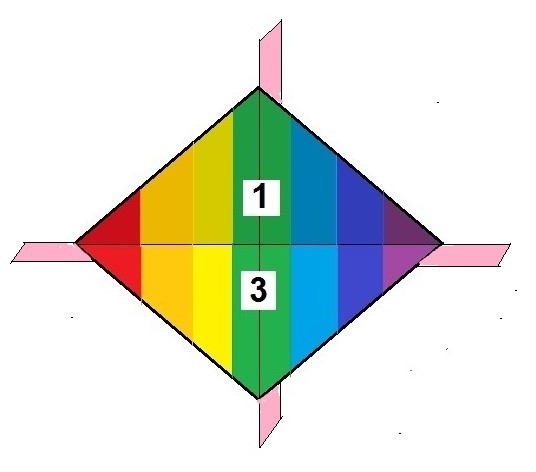
Los planos horizontal y vertical del Rombo

Hemos mirado al Rombo frontalmente. Ahora, al igual que hicimos con los ejes, nos queda observarlo apicalmente.

Si nos situamos arriba del Rombo y lo hacemos girar gracias al eje axial, observamos dos planos. A un plano, ya lo conocíamos porque es el plano que pasa por la diagonal menor, y el otro plano, es un plano nuevo que corre por las aristas superiores de la figura.

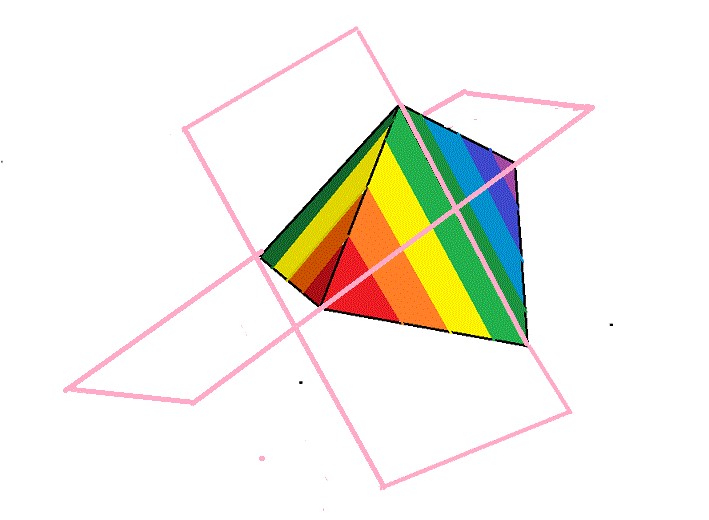
Un nuevo plano de simetría

Como sabemos, no hay como cambiar de perspectiva para ver las cosas de otro modo, así que ahora, en vez de mirar al Rombo de frente o desde arriba, lo haremos de perfil, mirando la figura desde el vértice agudo de la 1ª o 7ª dimensión.

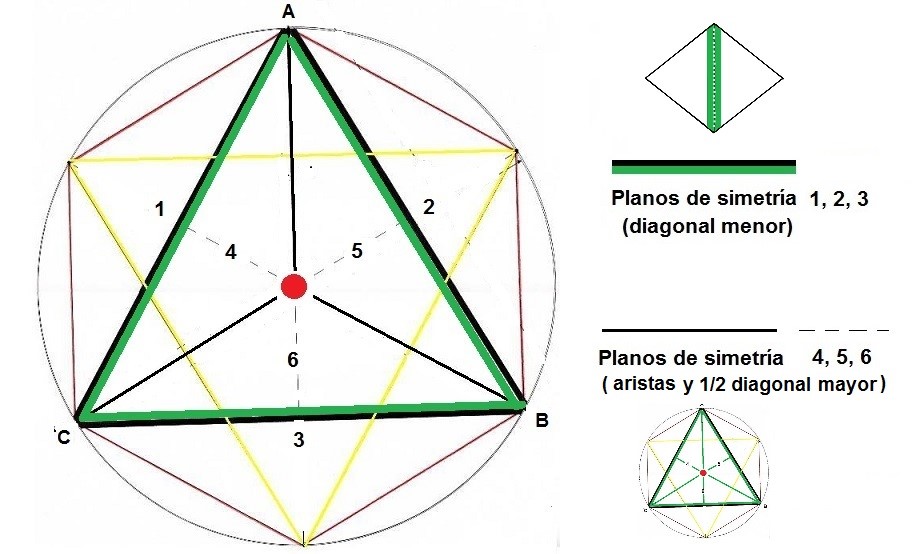
La figura tridimensional

Desde esta perspectiva, veremos de nuevo el plano de simetría perpendicular, el que pasa por las diagonales menores y que visto de perfil lleva los números 1,2, 3.

Dentro del triángulo verde ABC, (que representa el Rombo visto lateralmente), podemos dibujar sus tres ejes de simetría, (4,5.6), que si los proyectamos en el espacio, se convierten en sus planos de simetría.

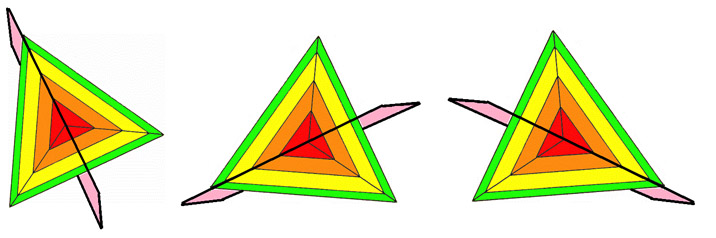
El plano de simetría también corta al Rombo por la mitad

Si cortáramos imaginariamente la figura del Rombo siguiendo estos tres planos de simetría, que atraviesan todo el Rombo y van desde el lado rojo al lado azul, obtendríamos también dos figuras perfectamente simétricas separadas entre si por su plano de simetría.

CONCLUSIONES

Todos sabíamos intuitivamente que había simetría en el Rombo, pero hoy hemos analizado un poco más esta cuestión y hemos descubierto conceptos nuevos. Hemos abierto el Rombo y hemos visto una parte de la simetría que había en su interior. Hay mucha más, no lo dudo, pero creo que ahora tenemos una idea un poco más clara y concreta.

Al final del estudio, hemos visto que tenemos la posibilidad de descubrir:

• Cara frontal del Rombo = 6 ejes de simetría especular
• Cara apical del Rombo =   6 ejes de simetría especular
• Cara lateral del Rombo = 6 ejes de simetría especular
• 1 eje de simetría axial
• 3 ejes de rotación no axial
• 6 planos de simetría desde la perspectiva frontal
• 6 planos de simetría desde la perspectiva apical
• 6 planos de simetría desde la perspectiva lateral

Es cierto que algunos ejes y planos están repetidos ya que se observan al mismo tiempo desde varios sitios a la vez y desde un punto de vista estricto y matemático, quizá no se puedan contar como tales, pero la intención del estudio era numerar todos los que son visibles desde cualquier perspectiva y que ofrecen una clara visión de simetría.

Bueno, ya sabemos lo que sabíamos. De hecho, lo único que hemos hecho ha sido observar y jugar con el Rombo, girándolo, dándole vueltas, poniéndolo de lado, de frente, de perfil y en cualquier otra posición extraña.

Hemos jugado con él y lo hemos mirado. De eso se trataba. El Rombo es simétrico. Si, ya lo sabíamos, pero quizás ahora somos más capaces de observar y disfrutar de la belleza desgranada de su simetría

EL ROMBO ES SIMÉTRICO

El Rombo es una forma geométrica capaz de explicarnos los principios físicos, matemáticos, concienciales y evolutivos de toda la creación. En él, está todo, y como reflejo de la Naturaleza que es, tenía que estar presente también dentro de si mismo un principio que se observa en todo el universo: La simetría.

La materia se presenta en el universo en innumerables formas, y podemos observar la presencia de la simetría en casi todas ellas: galaxias, estrellas, planetas, minerales y seres vivos.

La simetría por definición es un rasgo característico de formas geométricas, sistemas, ecuaciones, objetos materiales o entidades abstractas, relacionada con la invariancia bajo ciertas transformaciones, movimientos o intercambios.

Todos tenemos presente el concepto de simetría geométrica, pero la simetría en sí misma, es conceptualmente mucho más amplia y puede abarcar manifestaciones tan distintas como la arquitectura de una galaxia, la belleza de una pintura, la armonía de una partitura musical, la rima de una poesía, la igualdad de una ecuación matemática, y el equilibrio de un razonamiento lógico o de una ley física.

La simetría gobierna las leyes fundamentales de la física y constituye un principio matemático básico para comprender la estructura del universo.

La definición científica de simetría parece un poco fría, pero es la base para la comprensión de la teoría de las supercuerdas, la mecánica cuántica, la teoría de la relatividad, el Big Bang o la ley de la conservación de la energía.

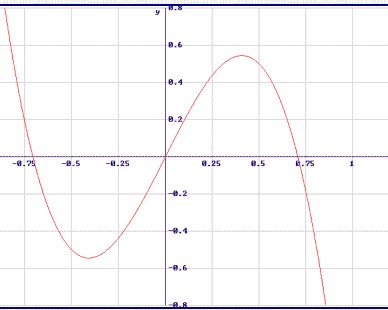
Simetría de una función matemática

El Rombo es simétrico y gracias a él, entendemos la simetría Espacio- Temporal que se da en las dimensiones paralelas, la simetría entre Materia y Energía que se da entre unas dimensiones y las otras, entre unos planos de conciencia y los otros, entre arriba y abajo, entre derecha e izquierda y entre el microcosmos y el macrocosmos, entre la acción y la reacción, entre la causa y su efecto, entre el principio y el final. En el Rombo la simetría es un principio omnipresente y su simetría arquitectónica es una pequeña muestra de lo que en realidad representa: La simetría de lo manifestado.