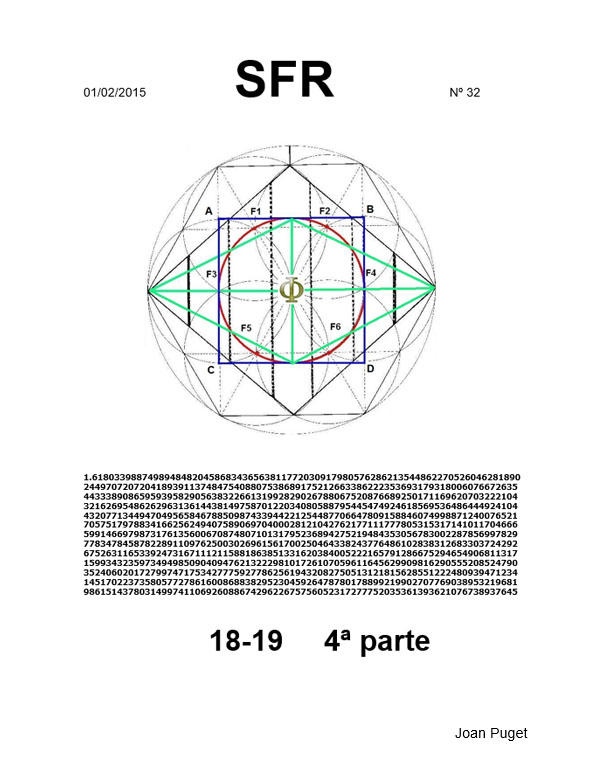
18-19 ( 4ª parte)

Introducción

Son muy pocos los números que tienen el honor de tener un nombre propio. De hecho, no tengo ningún inconveniente en decir que conozco poquísimos números que hayan sido capaces de haber recibido el gratificante y notable premio de un nombre. El primero de los números nominados que me viene a la cabeza es el número Π.

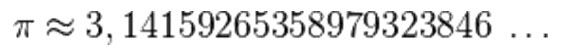
Al número Π lo conocí siendo muy joven y servía básicamente para introducirse adecuadamente en el mundo de la geometría. Era un número curioso, infinitamente largo, pero a efectos prácticos y de cálculo, era simplemente 3,1416. Con los años, descubrí que encontrar su verdadero valor había sido muy difícil, y que él, era el origen del famoso problema filosófico de la cuadratura del círculo.

La cuadratura del círculo

Al cabo de bastantes años, ya totalmente fuera de la etapa educativa colegial, y a causa de la curiosidad propia, conocí a otro número, también con nombre propio. Se trataba del número ɸ.

Estos dos extraños números Π, y ɸ, a pesar de ser tan distintos y estar relacionados con funciones tan alejadas las unas de las otras, tenían una característica común: Eran números irracionales, ya que se caracterizaban por poseer infinitas cifras decimales aperiódicas.

Nuestro nuevo número, Phi, era una proporción matemática, una razón. Tenía algo parecido a Π , en cuanto a su fonética y a su irracionalidad. Además, ambos números, estaban relacionados matemáticamente por algunas ecuaciones del tipo “aproximadamente igual a“.

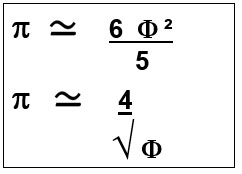
De la misma manera que Π, el número ɸ, tenía una evidente orientación geométrica, pero, tenía, además, una cierta vocación de estética, de armonía, de fórmula de crecimiento eficaz de la naturaleza, de evolución y de filosofía.

El número ɸ me pareció desde el principio, estar envuelto en una mística y en una criptografía, una escritura oculta única. La verdad es que siempre me llamó poderosamente la atención. Para intentar desvelar el misterio, acudí a los libros de Matila Ghyka, que me parecieron tan completos e impresionantes, como impenetrables. Por razones que desconozco, he sido incapaz de profundizar en el tema de ɸ tanto como hubiera querido, pero siempre he profesado una gran admiración y un gran respeto hacia este número. Así que, en cualquier caso, y lejos de introducirme en un estudio completo y que me podría llevar demasiado tiempo, decidí que como mínimo, debía dedicar un ligero esfuerzo para ver si el número ɸ estaba presente en el Rombo.

Si el Rombo y en especial la figura con la que estaba trabajando desde el inicio de las investigaciones, la de diagonal menor de 19,05…era armónica, y estaba relacionada con el universo, con la creación de los reinos de la naturaleza y con la evolución, el número ɸ debía estar presente en algún punto de la construcción de la figura. Tenía que ser así casi obligatoriamente y debía buscarlo. Solo por pura y sana curiosidad.

Siempre ha habido una frase muy popular entre los estudiantes del Rombo que me ha hecho buscar la presencia de fenómenos muy diversos en la figura. Es una máxima que he oído en innumerables ocasiones y que, en cierta forma, de una manera continua, me ha supuesto un reto intelectual, para ver si era cierta del todo o no. Más o menos, la paremia, que se mueve entre el aforismo y el axioma, con todas las variantes, entonaciones emocionales y modificaciones rítmicas posibles, dice así:

“Todo está en el Rombo.”
“El Rombo lo contiene todo”
“Todo se encuentra en el Rombo”

Es una de esas frases que es muy fácil de decir, y muy difícil de demostrar. Particularmente, siempre, me ha “picado” y me ha dado un plus de motivación para iniciar cualquier estudio relacionado con la sagrada figura.

En este caso, también fue así, ya que el interés por descubrir a ɸ , apareció en el 2010, cuando estaba finalizando un artículo de dibujos, publicado en su día y llamado 18-19 2ª parte.

En aquel momento, mientras realizaba los cálculos matemáticos, para rematar definitivamente el estudio, me apareció por sorpresa ɸ y entonces, nada más acabar el número que tenía entre las manos, empecé a escribir un nuevo trabajo que finalizaría algunos unos meses más tarde, pero que no llegué a publicar. El artículo no se acabó del todo porque me faltaba retocar algunos pequeños detalles, hacer algunas comprobaciones… y sin más…. se quedó en el tintero, a la espera de una mejor ocasión.

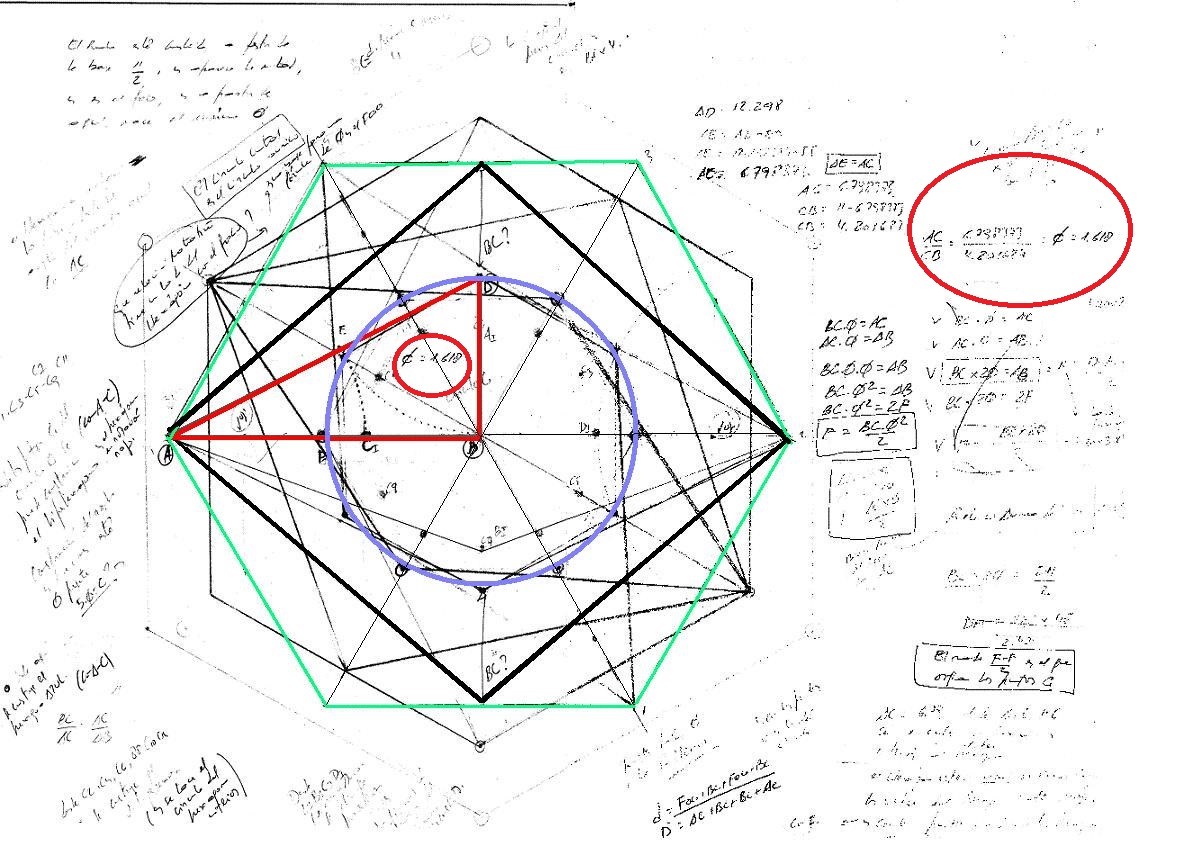
El dibujo donde apareció ɸ

Este complicado dibujo, apareció en el artículo del 2010 y era el preámbulo del trabajo que nunca llegué a presentar en sociedad. Ahora, al cabo de casi 5 años, creo que le ha llegado el momento de aparecer, aunque, está incompleto, ya que ha habido toda una serie de cálculos que no he querido publicar y algunos caminos que se han abierto mientras lo terminaba que no he querido andar para no sobrecargar de contenido el trabajo.

De tanto en tanto, y siempre con bastante separación temporal, van apareciendo artículos relacionados con la geometría y las matemáticas de la figura. Este escrito, ha seguido el mismo curso que los demás, y al acabarlo, también se han abierto las puertas para lo que podría ser la publicación de la 5ª parte… pero ya veremos si le llega su turno de aquí un tiempo…o si se queda en el cajón del olvido.

De momento, tenemos este nuevo escrito. Quería saber si se podía observar a phi y ver de dónde salía, de donde emergía este extraño número. Recordemos ahora brevemente su origen y presentémoslo en sociedad.

Origen del número áurico

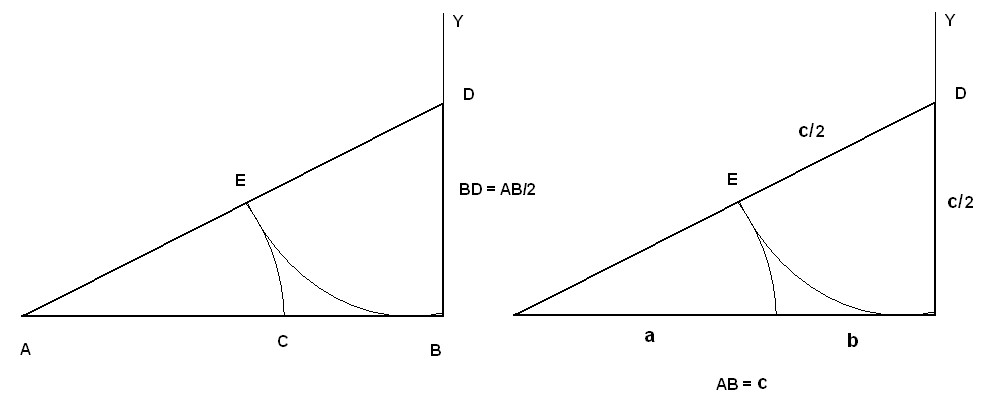
Su origen

Dibujamos la línea AB y proyectamos sobre BY otra línea de manera que BD sea la mitad de AB, con lo que BD = AB/2. Con un compás desde el punto D, hacemos un semicírculo BE. Desde A, realizamos otro semicírculo a partir del punto E. Nos queda la línea inferior del triángulo dividida en dos partes: El segmento AC (le llamaremos a), y el segmento CB (le llamaremos b). La suma de los dos trozos de la recta es la línea AB (a la que llamaremos c = a+b)

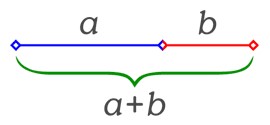
Tenemos un segmento c dividido en dos partes, a y b, de forma que la razón entre la totalidad del segmento y la parte a sea igual a la razón entre la parte a y la parte b.

Expresado matemáticamente:

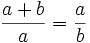
A esta razón, que cumple la propiedad, se le denomina razón o número áureos.

Podemos obtener matemáticamente este número a partir de la resolución de la ecuación anterior:

Bueno, pues hasta aquí, tenemos el nacimiento de una proporción y de un número. Nuestro objetivo era observar si en el Rombo concreto en el que hemos estado trabajando, el de 19.05 de diagonal menor, aparecía esta razón áurea.

Debo comentar que la línea de trabajo que seguiré en el artículo es la segunda que recorrí. En el primer intento de hallar ɸ dentro del Rombo, empecé a buscar sin ningún criterio matemático concreto, proporciones áuricas directas en la figura (entre un lado y otro, entre las diagonales, etc. etc.) y para mi desespero matemático, no encontré nada, no me apareció la razón Phi por más cálculos comparativos que realicé. Así que pensé que era mejor iniciar de nuevo el estudio desde otra perspectiva antes de acabar definitivamente con las pilas alcalinas de la calculadora y con la ya desgastada paciencia de mi cerebro. El encuentro casual de la proporción áurea en una de las innumerables operaciones hubiera orientado el trabajo hacia la primera línea de investigación, pero al no producirse, tuve que buscar un camino distinto por otro lado. Recordé una frase de Einstein que nos aconsejaba cambiar de forma de actuación cuando las cosas no salen bien:

“Si buscas resultados distintos, no hagas siempre lo mismo.”

En ese punto, me incliné a utilizar otro método. Estaba claro que para poder encontrar a ɸ , tenía que mirar atentamente a estos dos segmentos: a y b. Pensé que si eran tan importantes, posiblemente, todo el Rombo tenía que estar relacionado con el segmento a y también con el segmento b.

Quizá la hipótesis era una locura y no tenía ningún sentido, pero en el estado en el que estaba, tenía que probar algo totalmente nuevo. Para verificar la hipótesis, tenía que buscar si dentro de la construcción del Rombo, podía colocar en alguna zona, a estos dos segmentos, a y b que son los que al relacionarse, producen la razón Phi.

Pensé que una de las posibles maneras de encontrar algo, la más sencilla, era colocar directamente el triángulo áurico dentro del Rombo y ver que sucedía.

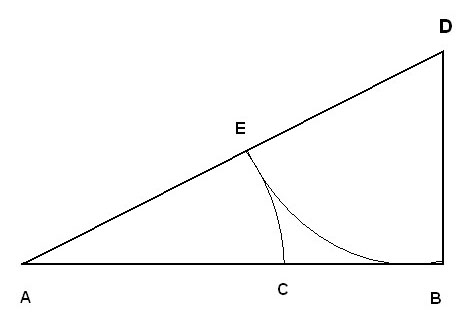
De entrada, vi que el triángulo podía tener cabida física dentro del Rombo. Una vez coloqué el triángulo en el Rombo, observé el resultado y vi que aparecían dos cosas que me gustaban. Por un lado, el cateto mayor del triángulo del estudio podía situarse perfectamente sobre la parte izquierda de la diagonal mayor. El cateto mayor del triángulo rectángulo tendría 11 cm. y el cateto menor, y por construcción, justo la mitad de esa cifra, es decir 5,5 cm, y arrancaría desde el punto Hara del Rombo, siguiendo el trayecto ascendente de la diagonal menor.

Ambas cifras, me sonaban muy bien, pues el número 11 es la mitad de 22       (Diagonal mayor) y 5.5 también, ya que es la distancia a la que se halla el foco desde el punto central del Rombo. Así que, siendo dos cifras muy importantes en la construcción de la figura del Rombo, había algo que, en principio, resultaba estético, parecía que otorgaba algunas posibilidades y con un poco de suerte, quizás podría encontrar algunas relaciones.

Para poder encontrar a ɸ , tenía que mirar y estudiar mucho a los dos segmentos que originan la relación: a y b. Así que me puse a trabajar. Lo primero, fue transformar un concepto, una ecuación de ɸ, en números reales y concretos con los que poder trabajar matemáticamente y constatar las realidades acerca de las suposiciones. Todo el trabajo que sigue a continuación no es más que el desarrollo de esa idea inicial de búsqueda de estos dos segmentos por doquier. Iniciaremos el tema plasmando en números la razón de ɸ e iremos llevando la búsqueda a las distintas zonas que forman la figura: la Diagonal mayor, la diagonal menor, las líneas de las dimensiones etcétera… etcétera… para ver si por algún lado, aparece escondida la dorada relación entre los segmentos y las líneas que constituyen el armazón del Rombo.

CALCULANDO LOS VALORES NUMÉRICOS DEL TRIÁNGULO

Como si se tratara de un problema elemental de geometría, vamos a encontrar gracias al cálculo Pitagórico, los valores de este triángulo rectángulo.

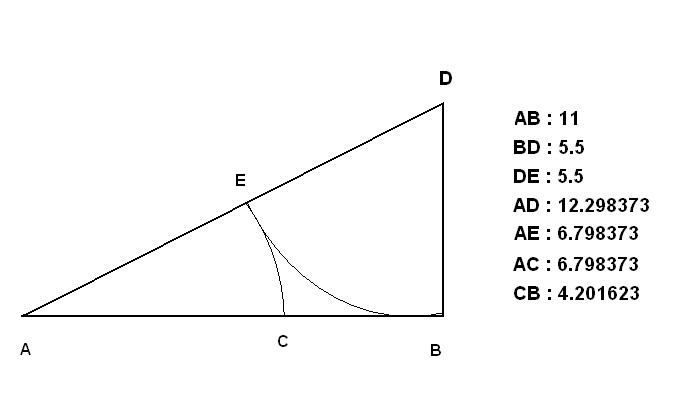
El triángulo áurico y sus medidas

AD = √AB ²+ BD²

AD = √ 121 +30.25

AD = √ 151.25

                

AD = 12.298373

 

AE = AD – DE

AE = 12.298373 – 5.5

AE = 6.798373

AC = AE

AC = 6.798373

 

BC = AB - AC

BC = 11- 6.798373 = 4.201627

Estas cifras son las que nos ayudarán posteriormente a realizar cualquier tipo de comprobación que queramos hacer acerca de los resultados que hallemos. De esta forma, verificaremos si las conclusiones a las que llegamos bajo la forma de ecuaciones son correctas o no. Son cifras importantes y las deberemos mirar a menudo para saber si nuestras conclusiones matemáticas son exactas. Pasaremos ahora a estudiar las relaciones de las distintas partes constituyentes del Rombo con los dos segmentos AC (a) y BC (b) para ver de qué tipo son las relaciones encontradas.

COLOCACIÓN DEL TRIÁNGULO ÁURICO DENTRO DEL ROMBO

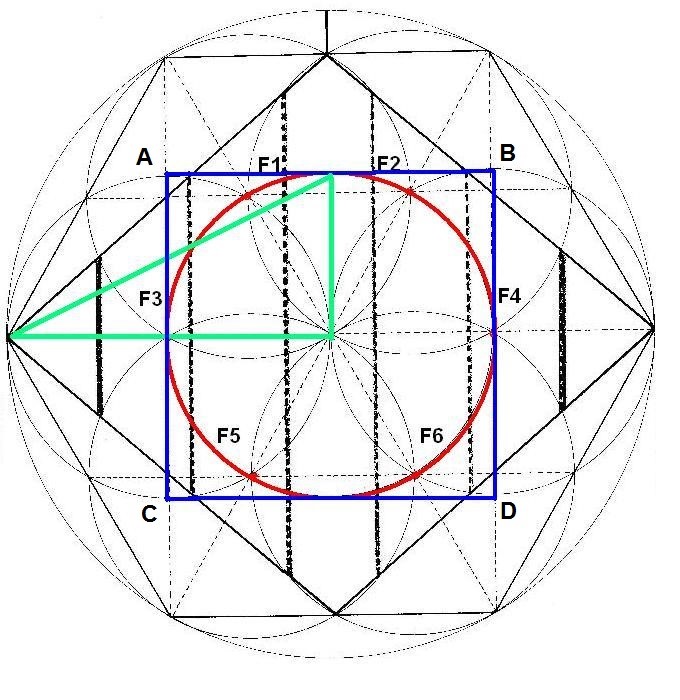
En color verde, observamos el triángulo áurico

Vemos en la parte más exterior del dibujo, la circunferencia madre, hecha con un radio de 11 cm. origen a su vez del hexágono circunscrito. Visualizamos también el Rombo con sus 7 dimensiones, halladas geométricamente a partir del Rombo y de sus intersecciones con las circunferencias interiores hechas a partir de los focos, de radio 5.5 cm.

Observamos el círculo rojo, que es vital para la construcción interior del Rombo, una especie de armazón, que unifica a todos los focos. En azul, observamos el cuadrado vinculado a la circunferencia interior y que nace también por las intersecciones de la construcción interna.

Para realizar el estudio matemático que vamos a llevar a cabo, partiremos de esta figura compleja y del triángulo áurico coloreado en verde que hemos colocado en su interior. Trabajaremos sobre este triángulo, que abarca la mitad de la diagonal mayor y un trozo de la diagonal menor, concretamente el segmento que va desde el centro hasta el punto de corte con el círculo rojo.

Primero, trasladaremos el triángulo y los valores buscados a una figura más sencilla. Es el mismo dibujo anterior, pero sin tanto estudio geométrico.

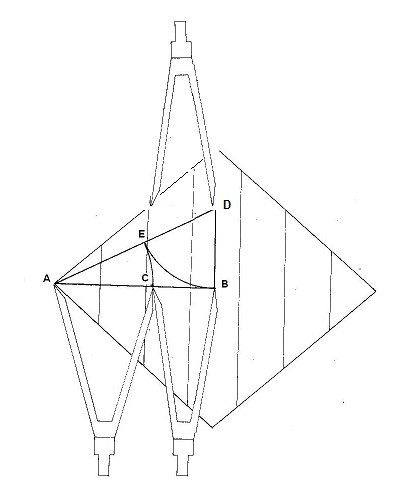
El triángulo áurico dentro del Rombo

Sobre la Diagonal mayor del Rombo que mide 22 cm, trazamos una recta AB de 11cm. Desde el punto B, trazamos hacia arriba otra línea BD, que, por definición del triángulo áurico, ha de ser la mitad de AB. Además, sabemos también que, por construcción, en este Rombo, BD medirá 5,5 cm. justamente la misma distancia que hay desde al centro al Foco.

Sigamos con la construcción de la figura. Desde el punto D, nos vamos hacia B y trazamos con un compás un semicírculo, que corta la línea AD en el punto E. Entonces, desde A, trazamos un semicírculo descendiente que partiendo desde E llega a la recta AB. En la intersección, aparece el punto C. Aplicamos la ecuación que hemos determinado anteriormente en el ejercicio algebraico y obtenemos la razón áurea que podemos seguir en la figura superior.

BC x ɸ = CA CA x ɸ = AB

1. LA RELACIÓN ÁURICA DEL FOCO

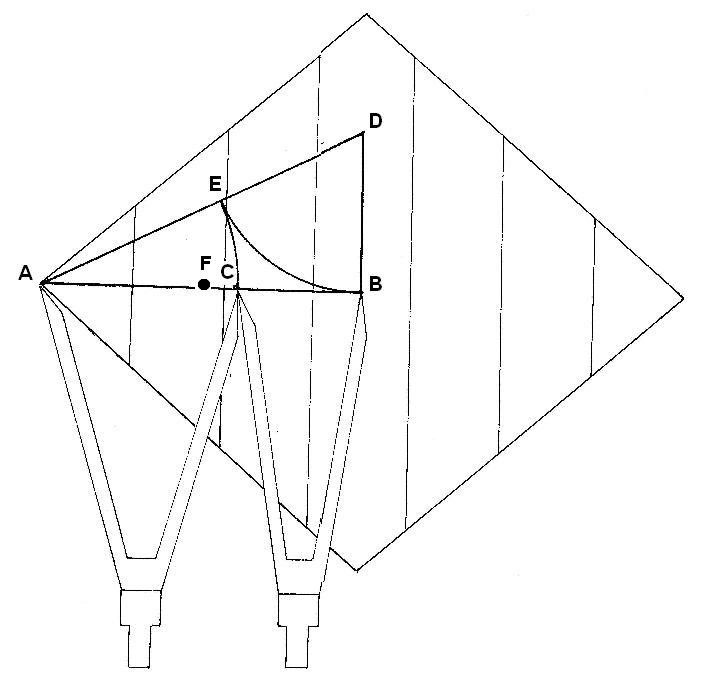
Colocamos al Foco en su posición por construcción, es decir, en el centro de la línea AB. Tenemos las relaciones conocidas:

BC x ɸ = AC       y     AC x ɸ = AB

Reemplazamos este segundo AC por el valor obtenido en la primera ecuación y podemos entonces, obviamente llegar a la conclusión que:

BC x ɸ x ɸ = AB                o lo que es lo mismo BC x ɸ² = AB

Como sabemos, el foco (5.5) es la mitad de AB (11), así que     BC x ɸ² = 2F

F =   BC x   ɸ²            _______             2

Sabemos que AB = AC x ɸ.     Como que AB = 2F, sustituimos

                         2F = AC x ɸ     Con lo que obtenemos F

F =  AC x ɸ        _______         2

Que son las razones áuricas entre el Foco y los segmentos. Este es un dato muy importante, porque el foco es el punto de equilibrio y de construcción de toda la figura. El foco guarda una relación áurica con los segmentos originales.

COMPROBACIÓN DE LA RELACIÓN ÁURICA DEL FOCO

F =   AC x F          _____           2

Reemplazamos por los valores conocidos:

AC = 6.798373

ɸ =  1.618033

                     F = 6.798373 x 1.618033 = 5.5
                                  ________________
                                              2

Miramos ahora la otra fórmula:

F =   BC x   ɸ²          __________             2

Reemplazamos por los valores conocidos:

BC = 4.201627

ɸ = 1.618033

           F = 4.201627 x 1.61803 ² = 5.5
                    _________________
                               2

2. LA RELACIÓN ÁURICA DE LA DIAGONAL MAYOR

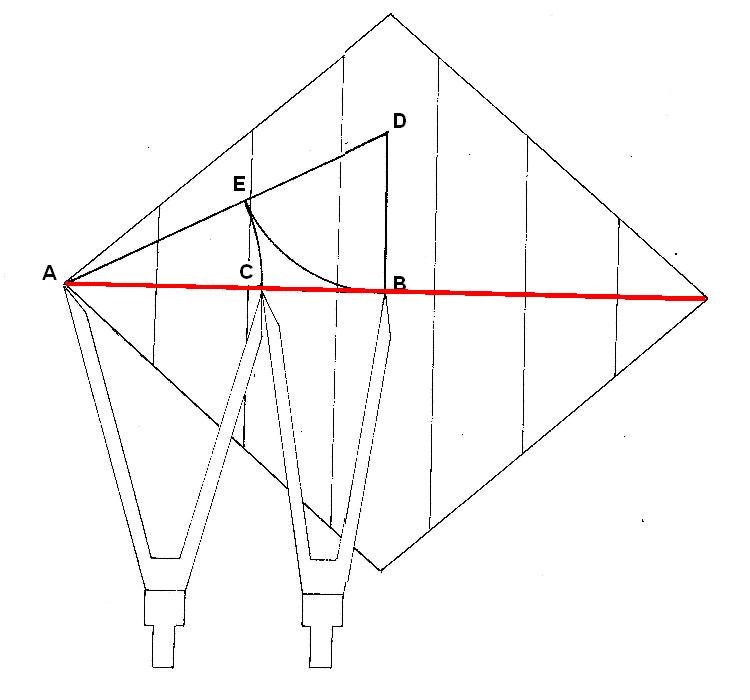
Sabemos por construcción que 4F = Diagonal mayor, así que

D = 4F         Reemplazando el valor de foco hallado anteriormente

D = 4   BC x F ²             o lo que es lo mismo
           ________
                2            

D = BC x 2 ɸ²

De igual manera, para obtener la otra relación, reemplazamos por el otro valor del Foco obtenido antes.

D = 4F          

            

D = 4 AC x ɸ                 o lo que es lo mismo
       _________
             2

D = AC x 2 ɸ

Lo que nos dice que la Diagonal Mayor del Rombo, está en relación áurica con los segmentos.

COMPROBACIÓN DE LA RELACIÓN ÁURICA DE LA DIAGONAL MAYOR

D = AC x 2ɸ

Reemplazamos por los valores hallados:

AC = 6.798373

ɸ =   1.618033

D = 6.798373 x 2 x 1.618033 = 22

D = BC x 2 ɸ²

Reemplazamos por las cifras conocidas

BC = 4.201627

ɸ = 1.618033

                                           D = 4.201627 x 2 x 1.618033 ² = 22

3. LA RELACIÓN ÁURICA DE LA DIAGONAL MENOR

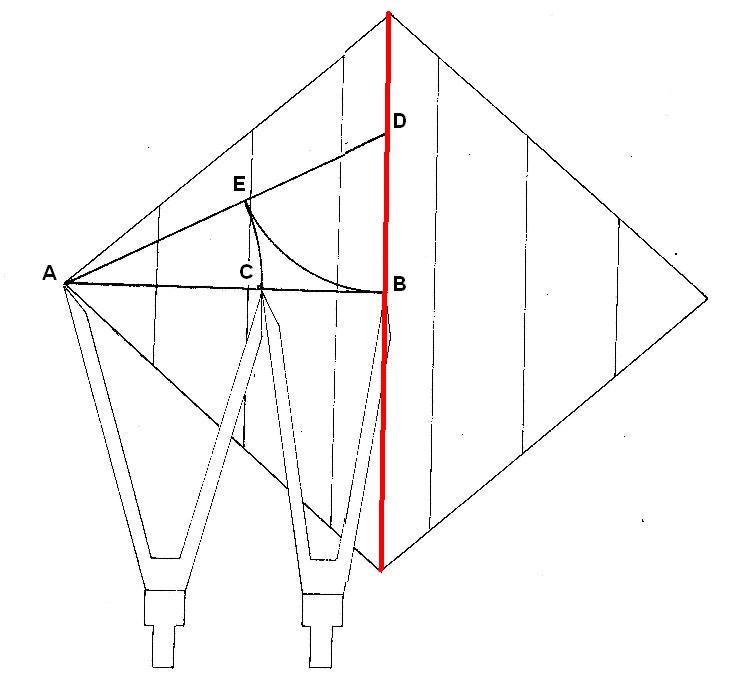
Conocemos la relación matemática entre la diagonal menor y la mayor. Si lo recordamos, vemos que:                  

d = D √3              substituimos el valor hallado de D y obtenemos
      ______
          2                   

d = AC √3   ɸ

d = 2AC x ɸ √3
       ___________
              2

Si buscamos la relación con el segmento BC, obtendremos lo siguiente:

d = D √3                substituyendo el valor hallado para D obtenemos
       ______
          2                         

d = BC √3   ɸ ²

d = BC x 2F ² x √3 
       ______________
                  2

Por lo que encontramos la relación áurica en la diagonal menor.

COMPROBACIÓN DE LA RELACIÓN ÁURICA DE LA DIAGONAL MENOR

Habíamos visto en el anterior artículo que la diagonal menor medía 19.05

Comprobaremos ahora este valor con el hallado con la relación áurica:

d = AC   √3   ɸ

d = 6.798373 √3   ɸ   = 19.05

Para el otro segmento:

d = BC √3   ɸ²

d = 4.201627 √3   ɸ² = 19.05

4. LA RELACIÓN ÁURICA DEL LADO DEL ROMBO

Partimos de un triángulo del que conocemos los dos catetos (Media Diagonal mayor y media diagonal menor) Hallaremos la hipotenusa que es el lado del Rombo marcado en rojo.

H ² = C ² + C ²      

h = √ ( AC √3 F/2) ² + ( AC F) ²

√ 7 h = AC    ____     ɸ           2

Ahora, repetiremos el cálculo para el otro segmento, el BC.

H ² = C ² + C ²     

h = √ ( BC √3 /2 ɸ ² ) ² + ( BC ɸ ²) ²

√7    h = BC       ____     ɸ ²              2

Por lo que también vemos la relación áurica en los lados del Rombo.

COMPROBACIÓN DE LA RELACIÓN ÁURICA DEL LADO DEL ROMBO

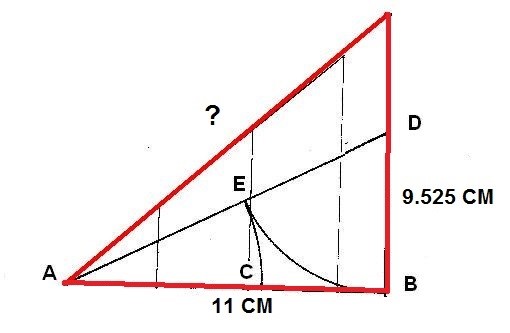
Observamos en detalle el lado del Rombo que queremos estudiar. Conocemos los dos catetos y buscamos el valor de la hipotenusa.                                              

h = √ ( 11 ) ² + ( 9.525)²

h = √ 121 + 90.725

h = 14.5

Reemplazamos los valores obtenidos:

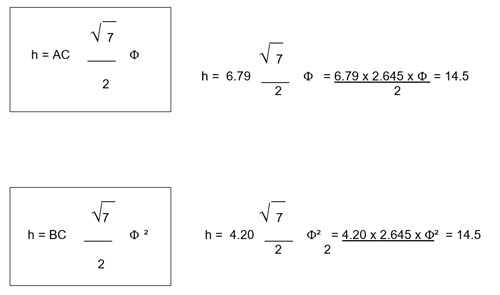
Por lo que también vemos la relación áurica en los lados del Rombo.

5. RELACIONES ÁURICAS DE LAS LÍNEAS INTERDIMENSIONALES

El desarrollo algebraico de todas estas operaciones, es un poco aparatoso y no tiene demasiado interés, así que solo exponemos el resultado final:  

Por lo que vemos que cada línea ínter dimensional está relacionada con Phi.

COMPROBACIÓN DE LAS RELACIONES ÁURICAS DE LAS LÍNEAS INTER DIMENSIONALES

Al hacer el cálculo, obtenemos los siguientes valores:

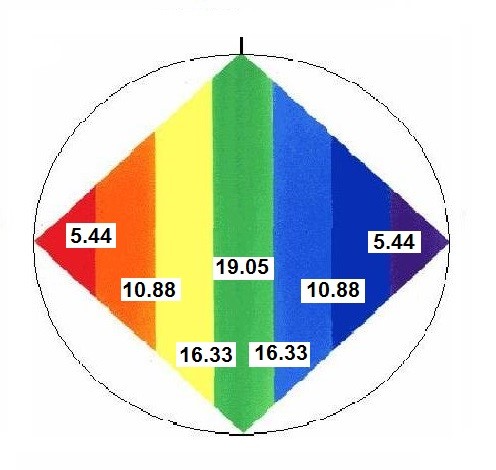
El tamaño de las líneas ínter dimensionales

6. RELACIÓN ÁURICA DEL ÁREA DEL ROMBO

La fórmula del área del Rombo es

               D x d
      A =    ____     =        

                  2                    

Sustituimos los valores hallados

Area = (AC 2ɸ) X ( AC √3 ɸ) = AC ² √3 ɸ²                                2

Para el otro segmento

Area= (BC 2ɸ²) x (BC√3 ɸ²) = BC ² √3  ɸ4                               2

COMPROBACIÓN DE LA RELACIÓN ÁURICA DEL ÁREA DEL ROMBO

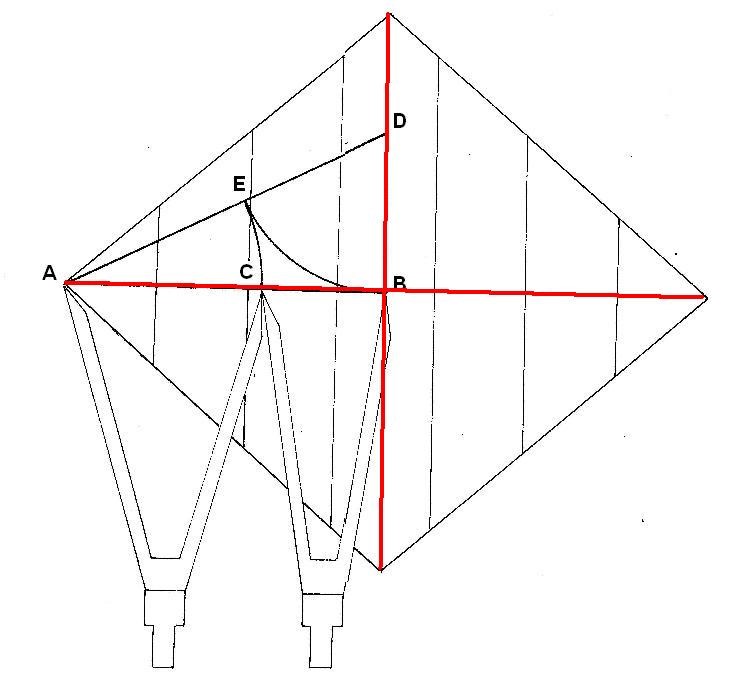
La fórmula del área del Rombo es

         D x d       22 x 19.05
A =     ____     = _________ =   209.5
            2                  2

Sustituimos los valores hallados

Area = (AC 2ɸ) X ( AC √3 ɸ) = AC ² √3 ɸ²                              2

Área = 6.79 x 6.79 x √3 ɸ² = 209.5                                            

Para el otro segmento

Area= (BC 2ɸ²) x (BC√3 ɸ²) = BC ² √3  ɸ4                                                                   2

Área = 4.20 x 4.20 √3   ɸ4 = 209.5

CONSIDERACIONES FINALES

El trabajo original del artículo era bastante más largo que este, porque incluía otros cálculos, como las relaciones áuricas de cada una de las dimensiones, pero creo que no venían a aportar demasiados datos nuevos, sino que en cierta manera, era una repetición matemática de todo lo visto hasta ahora.

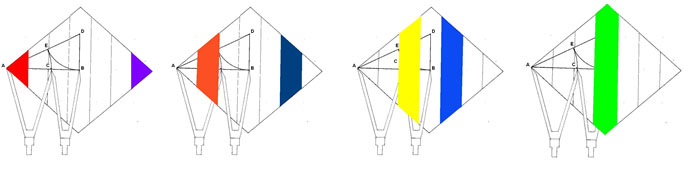
Tengamos presente que para determinar cada una de las áreas de las dimensiones, se ha de partir de una fórmula, que es el área del Trapecio:

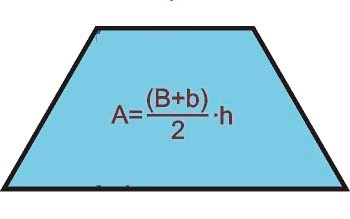
Y de cada una de las dimensiones, conocemos los valores de las líneas ínter dimensionales, así como la altura, así que el trabajo no publicado, no se trata más que de un ejercicio algebraico repetitivo, que precisa de muchas páginas para no aportar más que redundancias. De hecho, al hacer todos los cálculos para hallar la relación áurea de las dimensiones, tenía la misma sensación que tuve cuando realicé en su día, la larga serie de dibujos 18-19, en la que, a partir de un cierto número de dibujos, no se obtenían ya más datos de valor y todo se transformaba en una especie de juego recreativo. Es por eso que quizá, publique todos los otros datos en un futuro, en otro artículo, junto con algunas otras observaciones de la figura, pero no quiero hacer demasiado pesado el artículo, y creo que, con los datos aportados hasta ahora, ya se podrá mejorar un poco más la comprensión de la figura.

En principio, después de haber realizado las primeras determinaciones matemáticas y haber visto que todo el Rombo, con sus partes primordiales, se podía construir con el segmento a y con el segmento b, podía dar por finalizado el estudio, ya que era evidente la presencia matemática de ɸ.

Había observado con los cálculos hechos, que cualquiera de estos dos segmentos, si se multiplicaba por algún factor de ɸ, originaba todo el Rombo, toda su geometría interna. Se creaban así las dimensiones, los lados, los focos, las líneas ínter dimensionales y las áreas. Todas las partes de la figura, aparecían al multiplicar a o b por un factor numérico variable y por el número áureo. Si tomaba el segmento a = 6.798373, o el segmento b = 4.201627 y lo hacía interactuar matemáticamente con algún factor variable y con ɸ, aparecían todos los distintos valores constituyentes del Rombo.

Todo el Rombo de 22 cm de Diagonal Mayor y 19.05 cm de diagonal menor, se puede construir, por ejemplo, a partir del segmento a=6.79. Pero si por algún motivo, cambiamos, el valor inicial del segmento a por cualquier otro valor aleatorio, como por ejemplo a=1, obtendremos entonces un Rombo distinto en tamaño, pero con la misma proporción. En ese caso, la Diagonal Mayor valdría D=1x2ɸ = 3.23 y el valor de la diagonal menor sería d= 1x√3ɸ = 2.80 pero la razón entre la Mayor y la menor seguirá siendo la misma: 2 / √3.

De hecho, no es la medida del Rombo lo más importante, sino la proporción entre todos sus constituyentes. Un Rombo armónico, se puede construir de cualquier tamaño, pero se ha de partir de un valor inicial determinado con el que vamos a trabajar. Este valor primario, este segmento constructor primigenio, puede ser cualquier cifra, pero si tiene el valor a = 6.798373, la Diagonal mayor, medirá 22. Con cualquier otra cifra, el valor de la Diagonal mayor será distinto, aunque el Rombo tendrá las mismas proporciones interiores y será idéntico en cuanto a leyes.

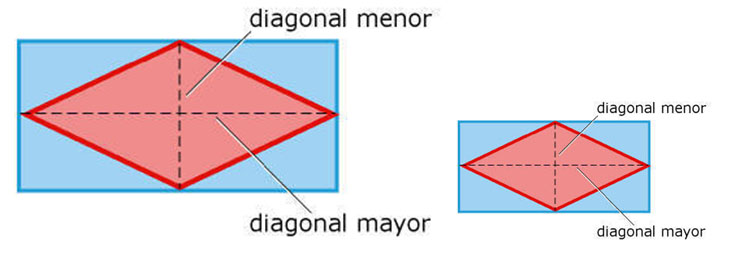
Diagonales mayores y menores

Podemos hacer un ejemplo para observar esto con más claridad. Estudiaremos el valor de las líneas ínter dimensionales con el valor inicial del segmento a = 6.798373 y luego, realizaremos el mismo cálculo, pero al segmento a, le daremos el valor de a=1. Observaremos los cálculos y veremos que los Rombos resultantes, aunque distintos en tamaño, tienen la misma proporcionalidad y razón.

COMPROBACIÓN CON LOS DISTINTOS VALORES DEL SEGMENTO   a

Recordamos el ejemplo anterior en el que el valor de AC (a) era de

AC = 6.798373. Para este valor, obteníamos estas cifras:

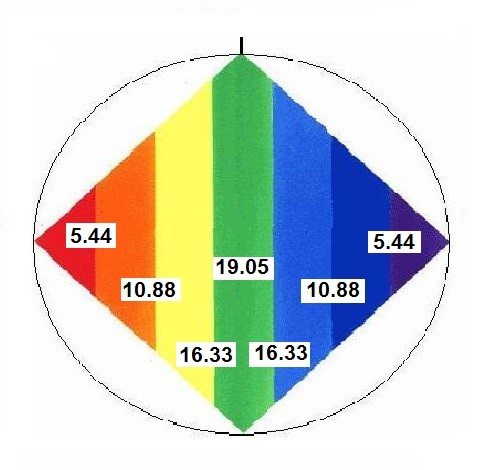
Rombo con valores obtenidos a partir de a = 6.798373

Pero si dibujamos otro Rombo en el que el valor de a=1, entonces, obtendremos las siguientes cifras:

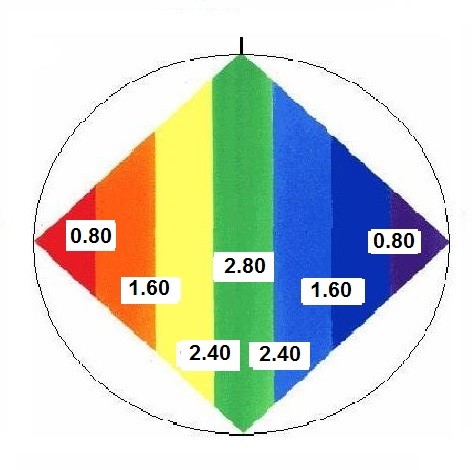
Las mismas razones

Este Rombo pequeño, mantiene las mismas razones entre sus distintos lados que las que tiene el Rombo mayor. Ambos Rombos, son distintos en tamaño, pero idénticos en proporciones. Son el mismo Rombo, pero su valor total es 6.798373 veces menor.

El valor de cada línea del Rombo, de cada área, resulta de la multiplicación del valor del segmento constructor primario, con los distintos factores de ɸ y con el mismo número ɸ .

Valor de una línea = Valor segmento constructor x Factor de ɸ x ɸ

El factor de ɸ, es el valor que multiplicará a ɸ, y será lógicamente lo que determinará las diferencias finales y las razones de los valores hallados.

ɸ, es constante y está presente en todas las ecuaciones. Lo que determina realmente el valor final de las líneas, es la razón variable que multiplica a ɸ. Ese factor es siempre distinto para cada línea y es el que hará que una línea sea mayor o menor respecto a la otra, pero siempre un número racional ɸ de veces.

La idea inicial del trabajo era encontrar alguna presencia del valor ɸ en la construcción de la figura. Al final del desarrollo del ejercicio, se ha encontrado una clara relación áurica entre el segmento original constructor y todos los valores numéricos que resultan de la construcción de las distintas partes del Rombo. Todos los segmentos, todas las líneas, todas las áreas están relacionados entre ellos por un número ɸ de veces. Y este hallazgo, creo que es el punto clave del estudio. Seguramente, el contenido más importante.

Creo que, con estos argumentos matemáticos, podemos decir con tranquilidad y certeza que la proporción áurea, se encuentra en todas las unidades constituyentes de la figura. El número ɸ está en todas la partes del Rombo. Allí está, agazapado, silencioso, sin apenas decir nada, inadvertido, escondido e invisible, como todo el conocimiento del Rombo. No se le observa dentro del Rombo a simple vista, pero a nuestra figura, hay que estudiarla, ver de lo que está hecha, razonarla, abrirla suavemente y entonces es cuando muestra contenta su enorme contenido. Su inphinito contenido.

ɸn