Las réplicas

Leonardo de Pisa, también llamado Fibonacci, fue un matemático italiano  que difundió en Europa  el sistema de numeración indo-arábigo y la sucesión numérica que actualmente lleva su nombre. Esta lista infinita de números naturales comienza con dos números cualesquiera de la serie y a partir de estos dos, cada número siguiente es la suma de los dos anteriores. La sucesión comienza con dos números naturales (dependiendo de la referencia se empieza con 0 y 1 en otros casos con 1 y 1)

0,1,1,2,3,5,8,13,21,34,55,89,144…EstaE

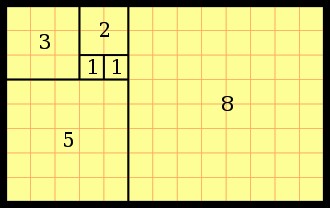
Esta construcción geométrica sigue la serie de Fibonacci.

Esta serie numérica tiene muchísimas características matemáticas. Por ejemplo, como curiosidad diremos que la serie tiene sólo tres números en los que durante la progresión aparezca su cuadrado perfecto: el 0 (0), el 1(1) y el 12 (144), números que desde el punto de vista de la metafísica del Rombo resultan muy interesantes, en especial el 12 ya que está vinculado con los 12 Rayos, las 12 notas musicales, los 12 grupos de 12 elementos y los 144 elementos primarios.

Esta sucesión de números tiene aplicaciones en las ciencias de la computación, en la teoría de juegos, en algunas configuraciones biológicas, en la dinámica de huracanes y en la organización de galaxias. Una de las curiosidades de esta sucesión de números es que la relación entre dos números consecutivos de la serie se acerca progresivamente a la relación áurea (ɸ = 1.618…) cuando los números de la serie avanzan y aumentan de magnitud.

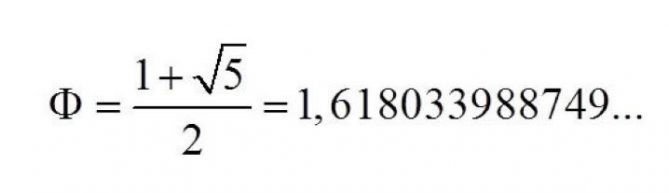
Si hacemos una sencilla comprobación matemática de los primeros números de la serie veremos que, poco a poco y en la medida en que avanzamos en la serie, el cociente entre el número que miramos y el anterior se aproxima cada vez más al valor de ɸ. Por lo tanto, podemos decir que, en la serie de Fibonacci la razón matemática entre dos números consecutivos de la serie tiende a ɸ cuando estos avanzan hacia el ∞.

Observemos a continuación la razón matemática entre los primeros números de

la serie y veremos como el cociente se va acercando progresivamente a ɸ en la medida en que los números avanzan en magnitud.

1/0 =0

1/1 =1

1/1 =1

2/1 =2

3/2 =1.5

5/3 = 1.666

8/5 = 1.6

13/8 = 1.625

21/13 = 1.615

34/21 = 1.619

55/34 =1.617

89/55 =1.618

144/89 =1.617

233/144= 1.61805

377/233= 1.61802

610/377= 1.618037

987/610= 1.618032

En el siguiente dibujo veremos un gran triángulo cuyo vértice está en el extremo de la primera dimensión (en rojo) y cuya base se abre cada vez más hacia la derecha llegando hasta la séptima dimensión. Y si quisiéramos ampliar un poco más el dibujo, podríamos ver como las aristas del Rombo en su proyección, podrían  prolongarse mas allá de la 7ª Dimensión del Rombo y alargarse hasta el infinito.

A partir de este concepto y con el mismo espacio que hay entre las dimensiones del Rombo (22:7=3.1428…) podemos dibujar una serie infinita de líneas paralelas. Sobre estos trazos verticales, marcaremos en color las líneas que siguen la progresión de Fibonacci y obtendremos una representación en la que se observarán las diferentes líneas de la serie, su separación y su valor.

Observaremos también los trapecios que se originan a partir de los trapecios originales del Rombo. Todos ellos están dibujados con la misma distancia interdimesional y las bases mayores y menores  de cada uno de ellos, se alargan hasta tocar la proyección de las aristas. A lo largo de toda esta serie inacabable de trapecios aparecen de vez en cuando unos que son distintos  y que están marcados en color. Estos trapecios son los  enmarcados  por las líneas de la serie de Fibonacci. Una línea de la serie forma la base menor del trapecio y la otra  la base mayor. Esta serie de trapecios empieza con los valores 1 y 2   y a partir de aquí, se empieza a desarrollar toda la serie, es decir que el primer trapecio estará enmarcado entre los valores L1-L2.

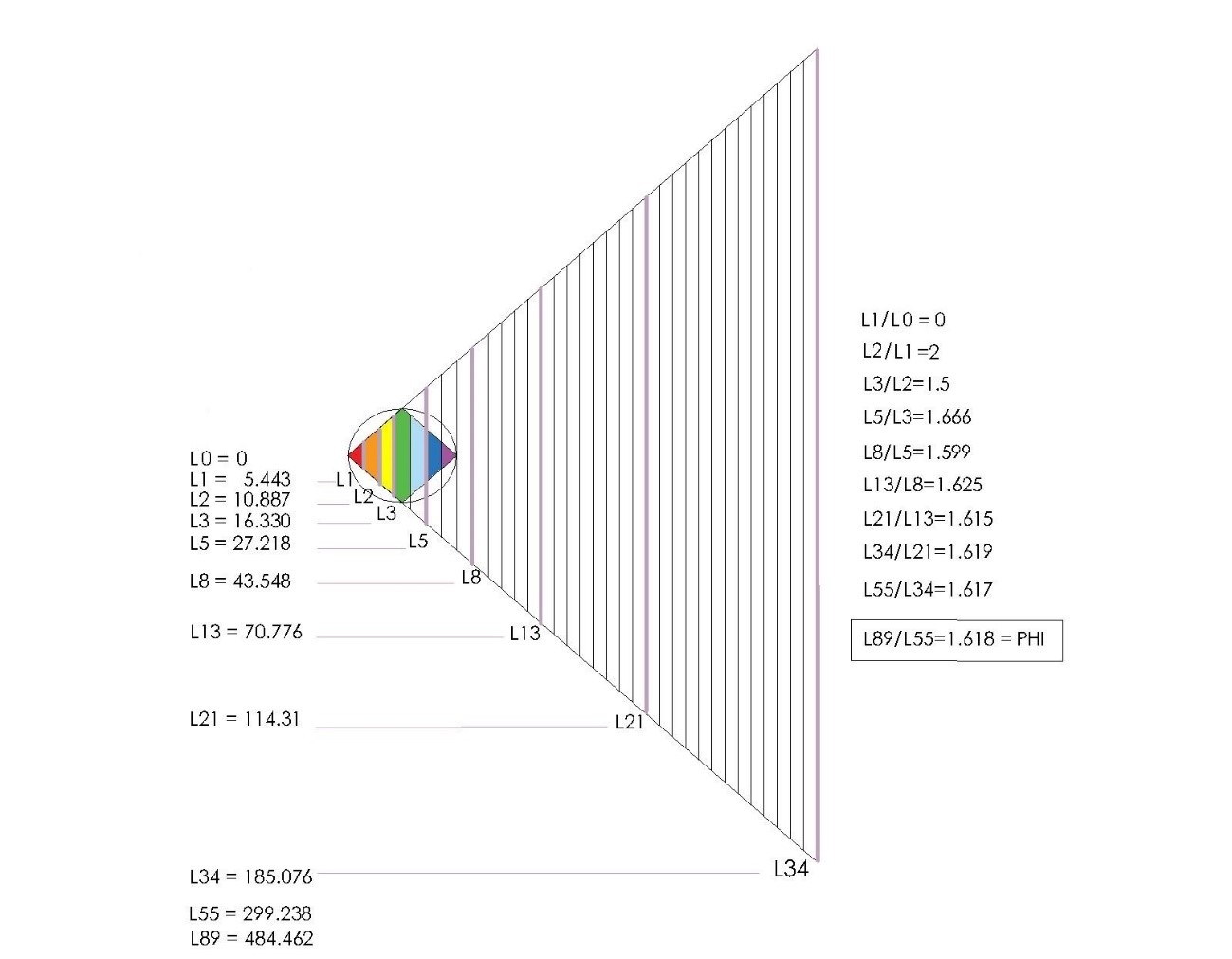
Los valores de las líneas de Fibonacci delimitan a los trapecios

En esta figura podemos ver como el tamaño de L0 = 0, el de L1 es 5.443, el de L2 es L1x2= 10.887, el de L3 es L1x3= 16.330, y fuera ya del área del Rombo, en el siguiente número de la serie, el valor de L5 es L1x5= 27.218.  Y si seguimos un poco más adelante veremos, por ejemplo, que el valor de L34 es L1x34= 185.076, el de L55 es L1x 55= 299.238 y el de L89 = L1x 89= 484.462

Vemos como el valor de la longitud de una línea cualquiera se halla multiplicando la longitud del segmento constructor L1= (5.443) por el número de la línea que estamos buscando. Observamos además como cada línea nueva se crea añadiendo una unidad L1 a la línea anterior. Esto sería el equivalente a ir haciendo una estructura en la que cada línea nueva tuviera una unidad más que la precedente, de manera que cada línea experimentara un crecimiento cuántico respecto a la anterior.

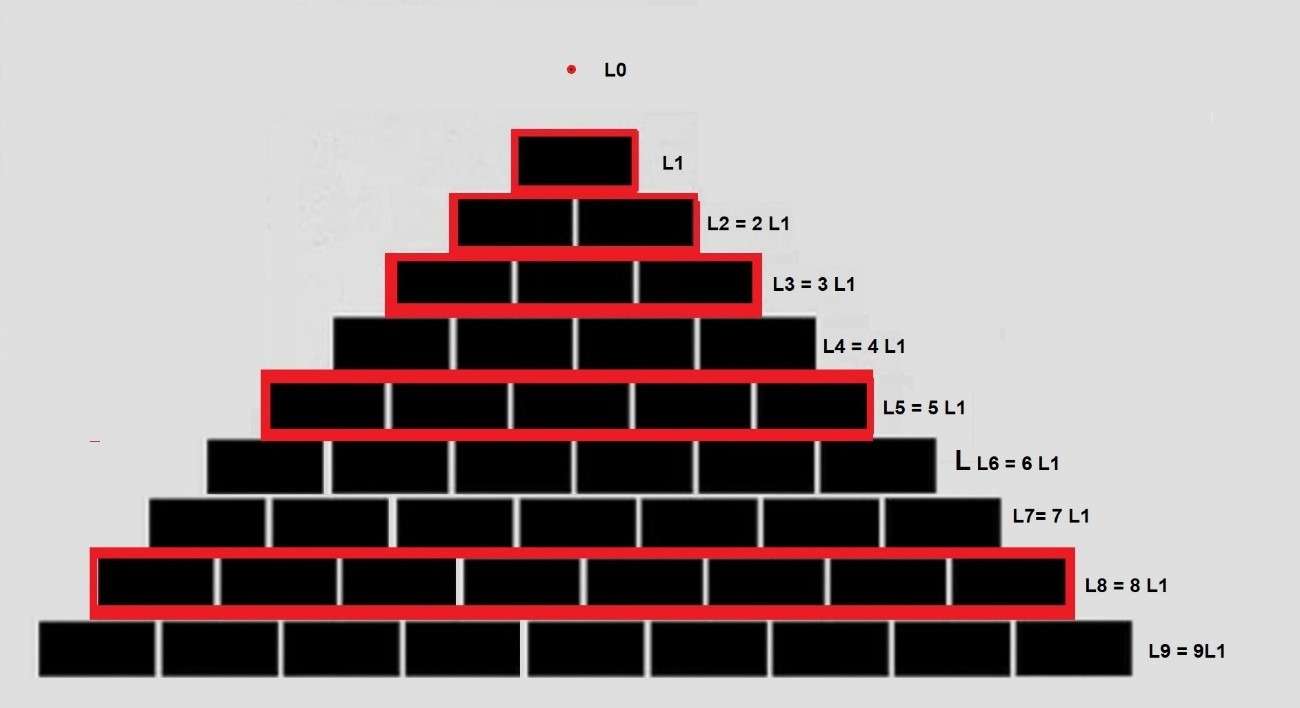
El crecimiento cuántico. En rojo las líneas de la serie de Fibonacci

Estas separaciones dimensionales siguen una progresión aritmética simple que es una sucesión de números tales que la diferencia de cualquier par de términos sucesivos de la secuencia es constante. En nuestro caso sería:  0, 5.443, 10.887, 18.330…

También podríamos calcular esta cifra multiplicando el valor de la línea inicial (5.443) por el número de cada línea y obtendríamos los siguientes datos:

L0= 0x5.443 = 0

L1= 1x5.443 = 5.443

L2= 2x5.443 = 10.887

L3= 3x5.443 = 18.330

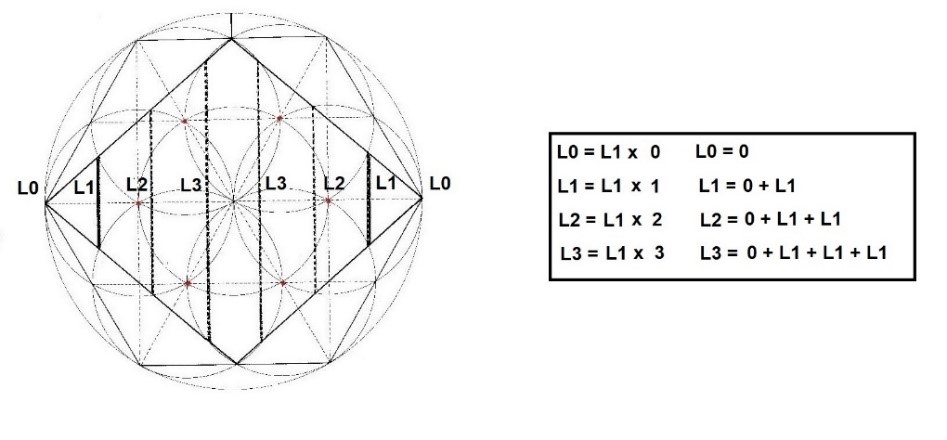
La serie aritmética de las dimensiones

LAS ÁREAS DE LAS DIMENSIONES DEL ROMBO

Con los datos que tenemos de las líneas inter dimensionales, podemos calcular las áreas del Rombo. Veremos que las áreas A1/A7 corresponden a un triángulo, las A2/A6 y A3/A5 son trapecios y el área A4 es la suma de dos semi trapecios.

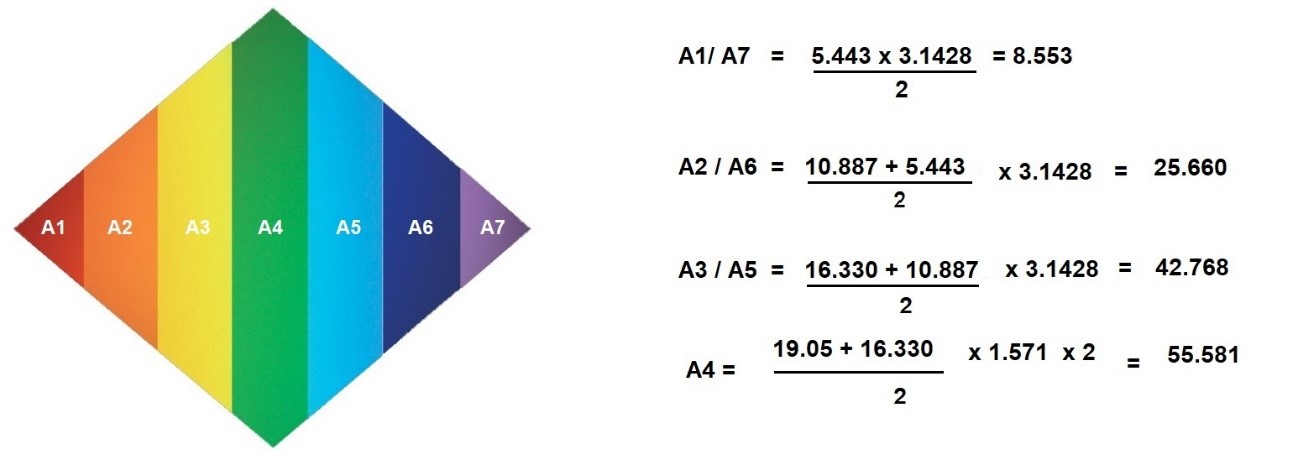
El valor de las áreas de las dimensiones

Y de estos datos, se desprende que:

A1 x 3 = A2

A1 x 5 = A3

A2 x 5/3 = A3

A3 x 3/5 = A2

Y en cambio, A4 no aparece en estas fracciones o múltiplos porque la progresión de crecimiento de la figura desaparece en A4. Sino lo hiciera y siguiese la serie de crecimiento aritmético de las otras áreas, el aspecto del área nº 4 sería éste y su nueva área tendría el valor de 59.873.

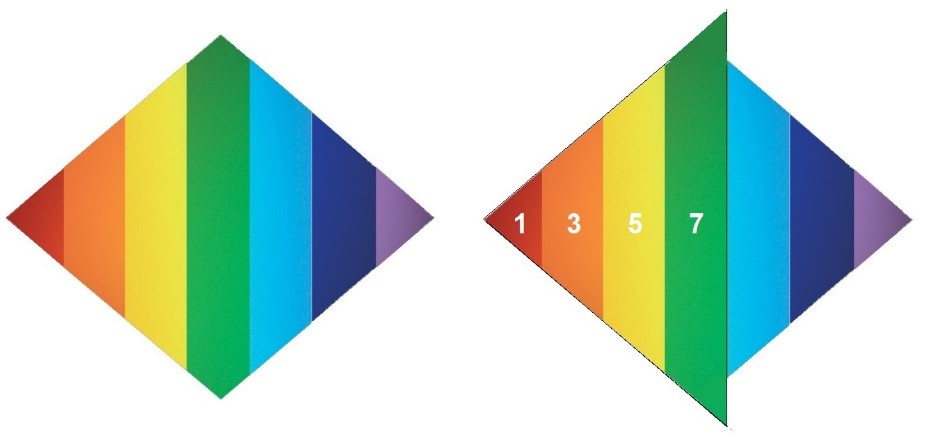
La progresión 1,3,5,7 con la cuarta dimensión expandida

En este caso, ya podríamos relacionar el área A4 con las otras áreas:

A1 = A4/7

A2 = A4 x 3/7

A3 = A4 x 5/7

Y el dibujo de la progresión de las líneas inter dimensionales quedaría así:

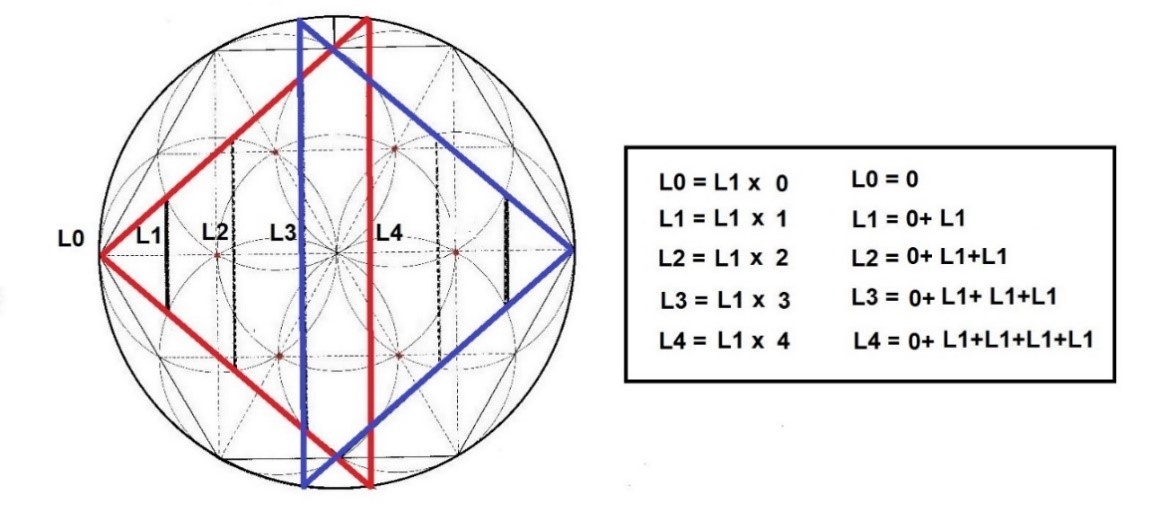
L4 contactaría con la circunferencia

Vemos que el espacio que ocuparía una hipotética L4 en la progresión del Rombo, (ya sea por la derecha o la izquierda) ya está ocupado por la L3 del otro lado. Este dibujo refleja también en cierta manera lo que sucede cuando hacemos incidir un haz de luz en un prisma. Por un lado, aparecen los colores rojos y por otro lado los azules. Al aproximar la parte caudal de ambas radiaciones y mezclarse aparece el color verde, que es una fusión de los últimos amarillos y azules.

LAS ÁREAS DE LOS TRAPECIOS DE FIBONACCI

Si prolongamos las aristas del Rombo nos van apareciendo infinitos trapecios separados por números naturales (0,1,2,3,4,5,6,7,8,9,10,11,12,13…) pero también podemos ver que aparecen distintos trapecios marcados en color que están separados por la serie de Fibonacci (0,1,2,3,5,8,13,21,34,55…). En el dibujo siguiente veremos al mismo tiempo las áreas de la serie natural y las áreas correspondientes a la serie de Fibonacci.

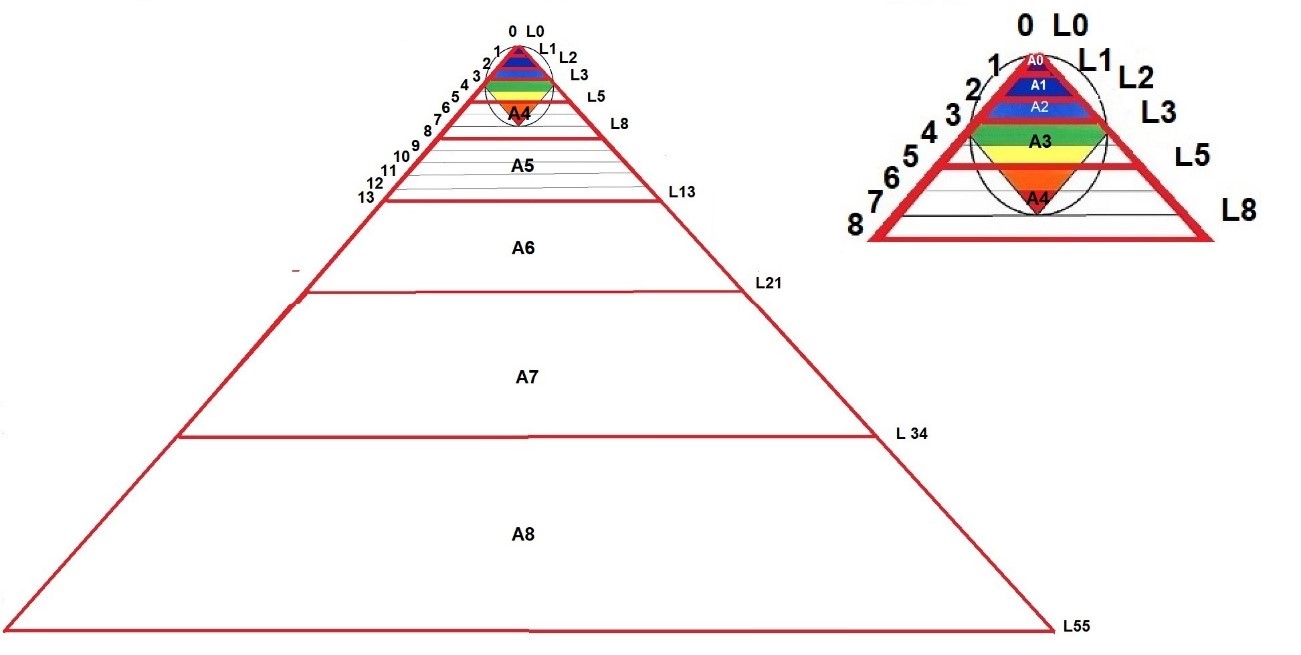
Los trapecios y su ampliación

Si queremos estudiar un poco más a estos distintos trapecios de la serie y observar que relación matemática existe entre ellos, tenemos que calcular sus superficies con la siguiente fórmula:

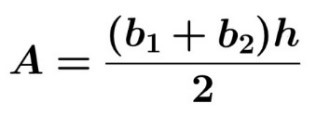
Este cálculo lo podemos hacer con las primeras líneas de la serie de Fibonacci (que están dentro del Rombo) y con todas las siguientes líneas que se encuentran ya por fuera de la estructura del Rombo. Veremos que cuanto más vayamos avanzando en la serie, los cálculos matemáticos referentes a las relaciones entre las áreas de los trapecios consecutivos se verán con más claridad.

Pero no todo son trapecios en el Rombo. En la 1ª dimensión hay un triángulo, que es una figura geométrica que se parece mucho al trapecio. La única diferencia es que el triángulo tiene una Base mayor que es un valor conocido y una base menor cuyo valor es 0. Entonces la fórmula del trapecio que es esta:

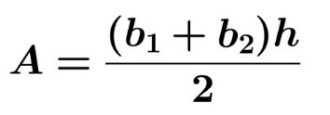
Sufre una modificación y queda de la siguiente manera:

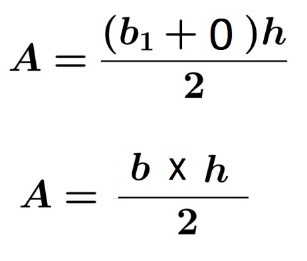
Con lo que podemos calcular el área del triángulo.

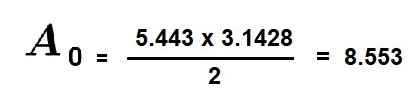
Seguidamente podemos calcular las áreas del primer trapecio de la serie y de los siguientes.

Al llegar a las áreas de cierto valor numérico, podemos comprobar con más claridad  que la razón matemática que existe entre el trapecio que estamos observando  y el que le precede en la serie (A7/A6)  empieza a tender muy claramente hacia ɸ2.

Las áreas de los trapecios contiguos se relacionan matemáticamente con ɸ 2

En la relación de las áreas de A7 y A6, podemos ver que el cociente es aproximadamente igual a ɸ2

Podemos generalizar y decir que, entre dos trapecios contiguos de la serie, el trapecio mayor, respecto al menor se encuentra vinculado por la razón ɸ2.

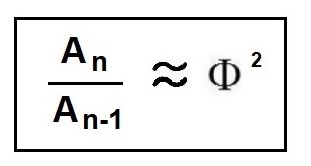
Y que en la medida en que se avanza por la serie y las áreas de los trapecios se hacen mayores y se acercan al infinito, la relación entre las dos áreas contiguas es ɸ2.  

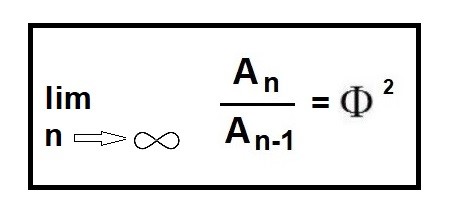
Con esta misma lógica y con la ecuación anterior, vemos que, si calculamos la relación que existe entre dos áreas no consecutivas sino separadas por otra área, la relación se multiplicará de nuevo por ɸ2 y aparecerá la relación ɸ4 entre las áreas de los trapecios no contiguos.

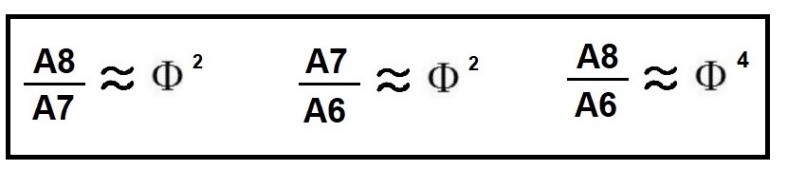
Estas relaciones de crecimiento se dan cuando comparamos un área mayor con una menor. Pero, naturalmente podemos buscar cómo sería el tipo de relación entre un área menor y una mayor. Para eso deberíamos tomar la anterior ecuación y modificarla. Pasaríamos de esta razón conocida:

Con esto vemos como el factor ɸ2 siempre está presente, en el crecimiento o el decrecimiento de la serie de trapecios. Para pasar de un trapecio pequeño a uno grande, se multiplica por ɸ2.  Y para ir de uno mayor a uno menor, se divide entre ɸ2.

LAS RÉPLICAS DE LA SERIE

Podemos pensar en la posibilidad de que en la medida en que una persona se va desarrollando (de una manera parecida a como lo hace la espiral de un caracol) y va pasando de un estado evolutivo simple a otro más complejo , va cambiando de frecuencia vibratoria y, por tanto, de número dentro de la serie. (1,1,2,3,5,8,13,21…)

Vitral en espiral de la Capilla de Acción de Gracias, Dallas, Texas

Cada número representaría una etapa concreta del desarrollo y llevaría consigo la información propia de esa estado particular. Además de llevar informaciones generales correspondientes a la fase que representa, los números podrían contener datos personales o de alguna situación concreta. Estos datos tendrían la posibilidad de poder ser transmitidos al siguiente número de la serie.  Así que, cuando el número 2 entrara en la serie para hacer el número 3 (1+2), haría que el número 3 llevara los datos heredados del número 2, (los generales y los particulares) y esto haría que toda la serie posterior 5,8,13…tuviera trazas de las informaciones proporcionadas por el número 2.

En la serie de Fibonacci, cada número nuevo de la serie se hace sumando el número del pasado al número del presente y entonces aparece el número del futuro, por lo que podemos pensar que las informaciones de los números de tiempos pasados pasan al presente y posteriormente se trasladan al futuro. La información transportada en los números no se pierde, sino que se mantiene viva y se transmite dentro de la serie.

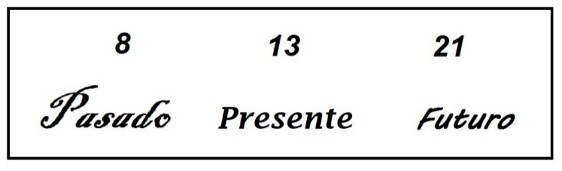
La serie de Fibonacci en su recorrido lineal recuerda a una línea de tiempo, donde los números se van sucediendo cronológicamente: 1,1,2,3,5,8… Esta línea de vida original en su desplazamiento y por un efecto de resonancia, crea réplicas extra dimensionales. En ocasiones, algún punto concreto de la réplica podría disparar una parte de su información sobre la línea de vida principal provocando una acción distorsionante que se iniciaría en el pasado y se proyectaría en el presente.

En el siguiente ejemplo, una experiencia muy impactante sucedida en la etapa 2 de la línea central de la vida, pasaría a una réplica dimensional y desde allí, en un momento determinado se proyectaría sobre la etapa 13 de la línea principal. Más adelante, en la etapa 34 tendría lugar otro suceso que dejaría huella y que quedaría marcado también en la línea replicante y desde allí, en un momento determinado y a causa de algún estímulo resonante se volcaría en la etapa 89 de la vida trayendo estímulos, informaciones o conflictos del pasado al presente.

Las proyecciones desde dimensiones paralelas a la línea de vida

La dimensión central de la vida y las dimensiones paralelas están estrechamente vinculadas. Y por muy alejadas que puedan aparentar estar, su conexión con la dimensión central de la vida es total. Por ello, se puede producir una transmisión de información de forma instantánea si el estímulo producido desde la dimensión central es suficientemente fuerte para que el recuerdo sea activado y llevado a la línea central de la vida.

LAS RÉPLICAS DIMENSIONALES

Ahora podemos regresar a nuestro Rombo original y construir una figura en la que se observen las distintas áreas que se forman con las líneas dimensionales de la serie de Fibonacci.

Si pensamos que el contenido del área A1 de Fibonacci, pudiese estar presente de alguna manera en el área A2, esta misma información también se podría hallar en A3 o cualquiera de las otras dos áreas de trapecios de la serie interior del Rombo (A3 - A4). Y con la misma razón, el área A5 podría contener la información de todas las otras áreas de los trapecios anteriores ya que ésta ha pasado por A1, A2, A3 y A4.

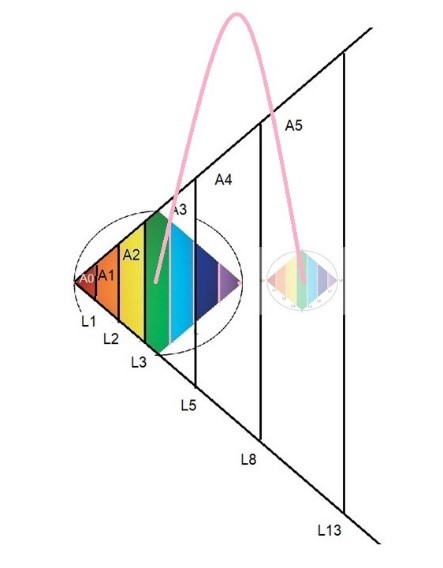
Las áreas de la serie de Fibonacci

Podríamos pensar entonces que una información escrita en una dimensión interna del Rombo se podría encontrar en una infinidad de dimensiones paralelas y externas al Rombo bajo la forma de réplicas de la información original. Y como los procesos en la naturaleza pueden tener dos caminos, (ida y vuelta) podemos teorizar que, para actuar sobre una situación localizada en una dimensión interior del Rombo, se podría hacer también desde una determinada dimensión exterior o paralela. Con esta idea, podemos suponer que las informaciones escritas en esas dimensiones paralelas podrían proyectarse sobre la dimensión original si por algún motivo el área en la que está la réplica se activara por alguna frecuencia resonante.

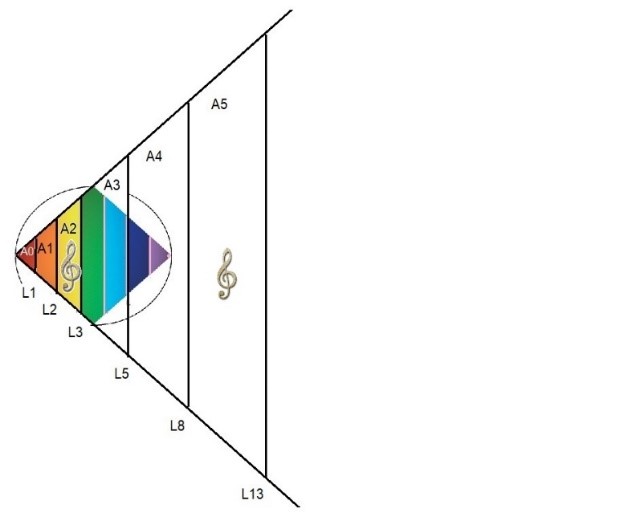
Las informaciones de una dimensión crean armónicos en otras dimensiones

En el caso del dibujo, una información grabada inicialmente en la 2ª dimensión (L2-L3) podría aparecer también en una dimensión extra dimensional y estar ubicada entre L8-L13.

LAS RÉPLICAS DE LA LÍNEA DE LA VIDA

Estos conceptos presentan similitudes con unas informaciones ancestrales que hablan de las distintas líneas de vida que existen al mismo tiempo.

Según este conocimiento, existe una línea de vida temporal central llamada Shantaná-Mirianá que es auténtica y que transcurre por el centro de la línea del tiempo de la vida.

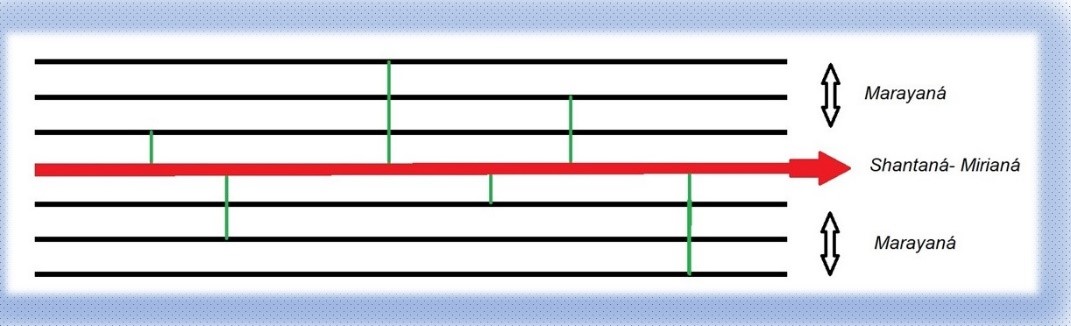
Las líneas de la vida

Esta flecha central por donde corre la línea del tiempo de la vida produce réplicas de sí misma observables en octavas de dimensiones de frecuencias superiores o inferiores, de tal manera que la información verídica de la línea se puede ver replicada en líneas de tiempo que fluyen en dimensiones paralelas y que son sólo un reflejo de la vida real. En estas líneas aparecen imágenes de la persona que son un alter ego, pues son una réplica, un segundo yo, y que es distinto de la personalidad original. Estas líneas llamadas Marayaná son ilusorias, pero desde ellas se puede incidir de alguna manera en la línea central. Estas líneas que corren por dimensiones paralelas pueden ser modificadas o alteradas por seres de alta frecuencia (pero no de amor y luz) que con su acción pueden confundir al ser humano desde ese nivel y producir acciones que lleguen a causar distorsiones y confusión en la línea central de vida.

LAS RÉPLICAS DE LAS PERSONALIDADES

A veces, algunas experiencias que han tenido lugar en el transcurso de una vida y que han dejado una huella muy fuerte, quedan grabadas en el alma y depositadas en dimensiones ocultas. Entonces, por la acción de algún estímulo que se presente en la vida actual y que entre en resonancia con la experiencia grabada, puede hacer que esas informaciones se reactiven, pulsen desde esa dimensión exterior, regresen de nuevo a la línea de la vida y provoquen desajustes de tipo emocional o mental. Estas alteraciones pueden aparecer y desaparecer ocasionalmente o mantenerse activas y pulsantes durante toda la vida, dependiendo de la intensidad en que ese impacto emocional quedó grabado en el alma.

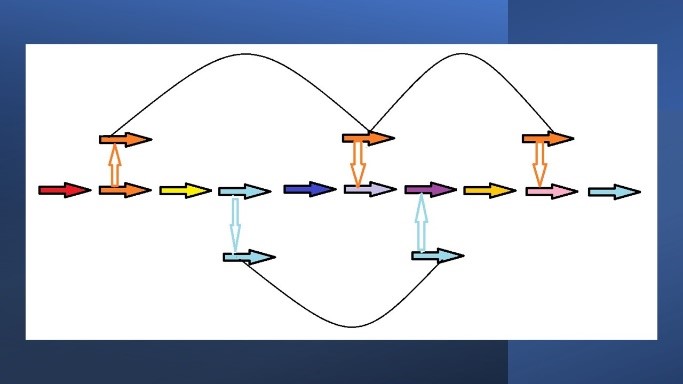
La pulsación de las personalidades de otras vidas

El alma por sí sola no puede borrar esos chips de conducta y si no ha solucionado esta perturbación estando encarnada, el problema (la personalidad) puede seguir adherida al alma como un ego con vida propia y presentarse en todas la vidas siguientes o en las vidas en las que tenga lugar un acontecimiento   que la haga resonar y esa impronta aparentemente dormida se reactive de nuevo.

Existen técnicas para corregir esa situación, pero a veces la solución no es fácil, sobre todo porque a veces, a una persona en un vida se le pueden acumular personalidades de diferentes vidas. En ese caso, su vida se vuelve difícil porque  reacciona con conductas fuera de toda lógica en situaciones que aparentemente son de fácil manejo.

Si una persona es conocedora de este problema, puede notar en que momento le detona esa personalidad, y en esa situación en concreto puede hacer dos cosas para solucionar o aliviar la situación: envolver en amor a ese ego que se presenta y deshacerlo totalmente o enviarlo de regreso a la dimensión desde donde llegó.

Dimensiones paralelas. Fotografía de Elsamuko

RESUMEN

Como hemos visto a lo largo del escrito, las mismas hipótesis de la creación de dimensiones paralelas portadoras de información reside en el caso de la serie Fibonacci, en los trapecios extra dimensionales, en las líneas de vida Marayaná, y en las personalidades. En todos estos modelos, hay acciones del pasado que han quedado guardadas y que se proyectan de nuevo sobre la vida presente de una persona cuando un estímulo intenso hace resonar una información ancestral y ésta se proyecta de nuevo desde una dimensión paralela a la línea de la vida.

Todo son ejemplos distintos del mismo hecho. Un suceso, una acción impactante o trascendente no se borra ni desaparece para siempre en el olvido. La fuerte impresión que ha tenido este hecho en la vida puede grabarse con fuerza debido a su gran carga emotiva y persistir fijado como recuerdo en dimensiones paralelas donde se crean las réplicas de lo ocurrido. Nada desaparece completamente. Todo permanece grabado y puede volver a ser revivido y traído al presente bajo determinadas condiciones. Si estas impresiones producen daño en la vida de la persona, han de ser reconocidas y limpiadas para dejar al alma sin cargas pulsantes. Mientras el alma arrastre impresiones y grabaciones como si fueran cadenas pesadas, no podrá gozar de libertad pues le impedirán transitar con comodidad por el sendero que haya escogido libremente.