La elipse y los focos
Este artículo se centra en el estudio de la circunferencia, de la elipse con sus Focos y de la onda senoidal.
LAS DOS SEMICIRCUNFERENCIAS Y LA ELIPSE
En el contexto del Rombo, la elipse tuvo una aparición y un desarrollo muy interesante. No nació de repente, sino que pasó por una gestación bastante larga y silenciosa. Cuando al principio la teníamos virtualmente delante, ni siquiera la supimos ver pues a la forma circular que se encontraba fuera del Rombo, que lo envolvía, y que se vinculaba con el Yin-Yang la llamamos inicialmente semicircunferencia o más exactamente doble semicircunferencia (representadas una en rojo y la otra en azul). Una circunferencia sola no podía envolver al Rombo. Tenían que ser dos semicircunferencias. Fueron varios los dibujos que se hicieron al principio hasta encontrar un diseño que fuera satisfactorio, y el modelo final fue parecido al siguiente:
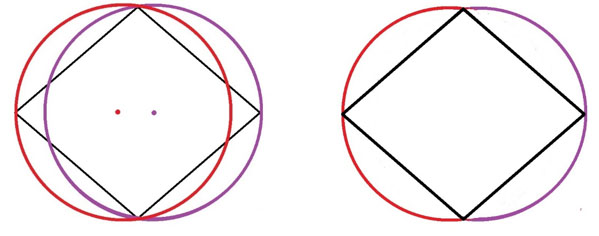
El dibujo con dos semicircunferencias
Aunque el diseño era interesante y expresaba correctamente la presencia envolvente de una fuerza Yin-Yang, el dibujo resultaba un poco extraño. Se entendía perfectamente la idea de que había dos semicircunferencias y que cada una de ellas iba desde el ángulo obtuso inferior hasta el superior pasando por el ángulo agudo. Pero, las dos semicircunferencias no se podían abrazar y fusionar perfectamente en la zona de los ángulos obtusos sin un cambio brusco de la curvatura de su línea porque no eran una circunferencia, sino dos, y cada una de ellas tenía un centro distinto.
Sobre la base de este dibujo inicial, vimos que existía otro diseño mucho más elegante, que fusionaba perfectamente a estas dos semicircunferencias y que proporcionaba mucha más belleza geométrica. En ese momento, la doble circunferencia (con dos centros) evolucionó geométrica y matemáticamente hacia la elipse (con dos Focos), que es la manera como se fusionan y se transforman las dos semicircunferencias en una sola línea para contener perfectamente al Rombo. La elipse, como veremos en el dibujo siguiente, transcurre un poco por dentro de las dos semicircunferencias y se ajusta perfectamente a los cuatro vértices.
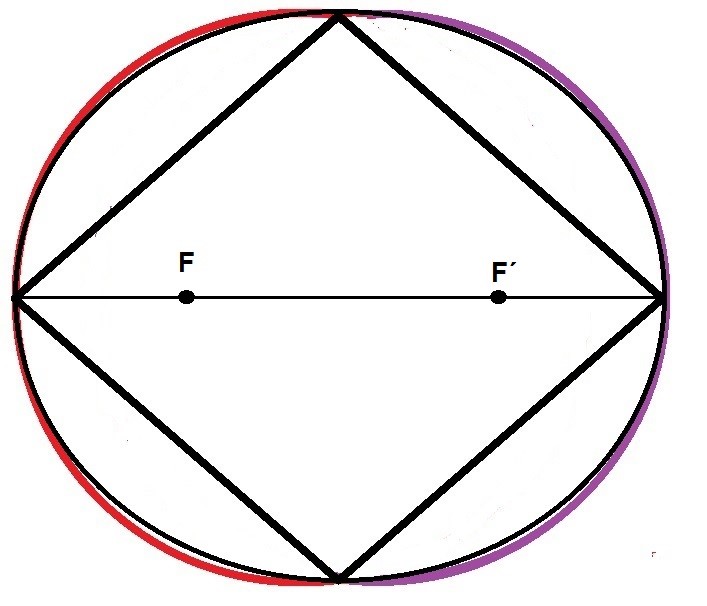
La fusión de las dos semicircunferencias en una elipse.
Al intentar comprender las ventajas que aportaba la elipse vimos que además de la forma estética y de la función matemática de la curva, la elipse hacía que necesariamente para su construcción debían aparecer en la Diagonal mayor sus dos Focos constructores y con ellos, toda la posibilidad de la geometría interna. Estas cuestiones nos hicieron ver que la elipse era la forma que mejor se adaptaba a la idea de que una curva tuviera dos polaridades que simbolizaban Yin-Yang y que estuvieran fusionadas sin ningún cambio brusco de curvatura. Por todos estos motivos, la elipse pasó a tener desde entonces un gran simbolismo (casi definitivo) dentro del esquema del Rombo.
Una elipse es (en cierta manera) una circunferencia que ha perdido la ubicación original de su centro exacto (O) porque éste se ha desplazado simétricamente hacia los extremos de la Diagonal mayor formando los Focos (F1- F2).
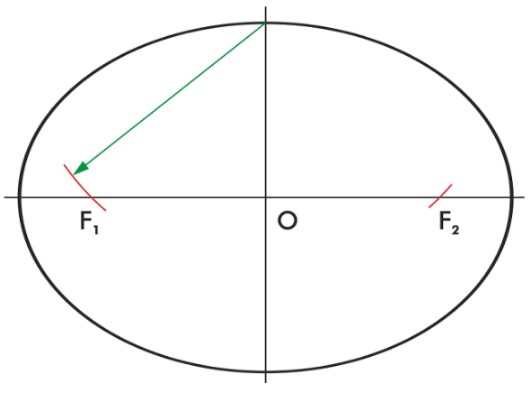
Los Focos de la elipse.
Aparte de los Focos, en la elipse, hemos de considerar a dos elementos muy importantes; el eje mayor D y el eje menor d.
En las elipses se cumplen las fórmulas aF1+aF2=D y bF1+bF2=D en las que vemos como las sumas de las distancias desde cualquier punto a los dos Focos es igual a la Diagonal mayor.
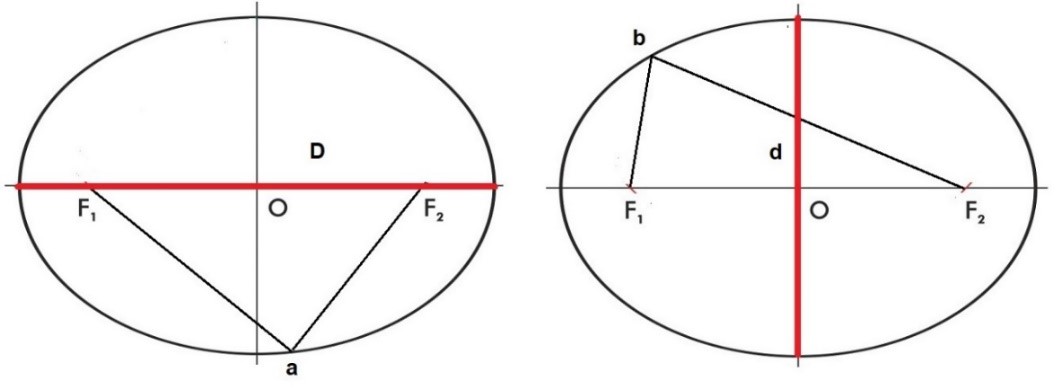
La Diagonal mayor y la diagonal menor de una elipse
Nuestro Rombo está contenido en una circunferencia madre y una elipse, que es una circunferencia que se ha adaptado para contener perfectamente al Rombo, y hace que los cuatro vértices del Rombo estén en contacto con ella. El radio matriz que nos ha permitido dibujar a la circunferencia y al hexágono, será el mismo que nos permitirá hallar los Focos del Rombo. Para determinarlos, se ha de tomar este radio creador y proyectarlo desde el vértice superior o inferior del Rombo (ID). Al hacerlo, se obtendrán dos puntos de corte con la Diagonal mayor que serán los puntos de Foco que permitirán posteriormente dibujar a la elipse.
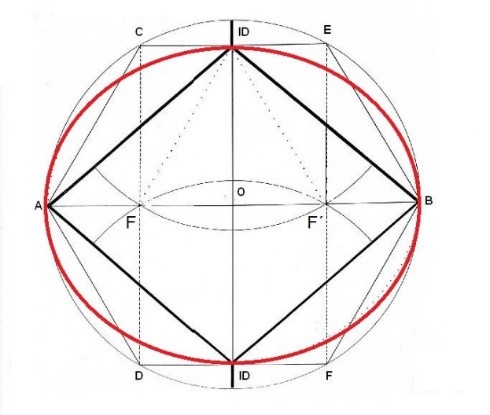
La obtención de los Focos
Aunque hay varios métodos dentro del dibujo técnico para crear una elipse, el sistema más sencillo de hacerlo (conocido como el método del jardinero) consiste en clavar una chincheta en cada uno de los dos Focos y unirlas con un hilo que tenga la longitud de la Diagonal mayor. Entonces, al desplazar el lápiz sobre el papel, se obtiene una elipse. {�=���=�2−�2
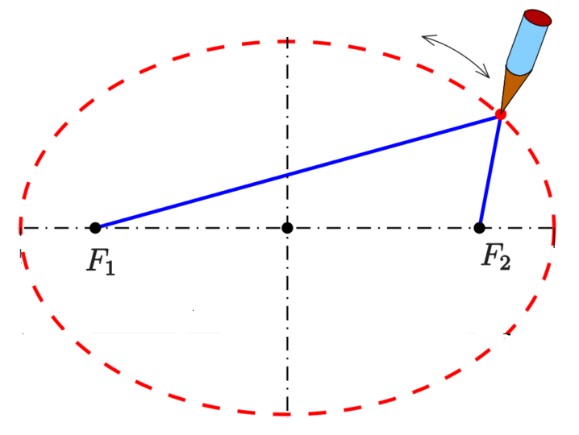
El método del jardinero
El Rombo no tiene un tamaño fijo, pues en condiciones fisiológicas, aunque su Diagonal mayor se mantiene estable (22 cm.) la diagonal menor puede oscilar fisiológicamente entre 18 y 19.9999 cm. Ello hace posible que podamos dibujar varios Rombos con sus elipses respectivas y que cada una de ellas tenga sus propios Focos.
En el dibujo siguiente veremos tres Rombos: uno mayor de color rojo, otro mediano de color verde y uno tercero más pequeño de color violeta. Representan las tres fases de la respiración del Rombo: la fase de contracción, el período intermedio y la fase expansiva. En la fase contractiva 1 (Rombo de 18 cm.) los Focos F1 están muy alejados del centro. En la fase intermedia 2 (Rombo de 19.05 cm.) los Focos F2 están en una posición intermedia y en la fase expansiva 3 (Rombo de 19.9999 cm.) los Focos F3 se hallan más próximos al centro de la circunferencia.
Para hallar a los diferentes Focos debemos ir a los puntos1,2,3 (que corresponden a los distintos vértices superiores) y desde allí y con el radio matriz, proyectar semicírculos hasta la diagonal mayor.
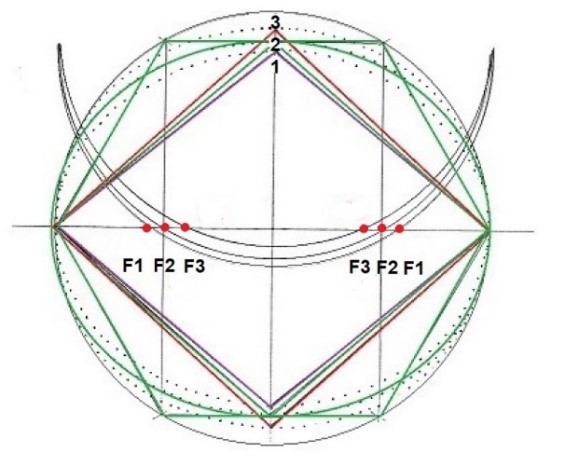
La localización de los Focos es móvil
En la medida en que el Rombo se va achatando, la excentricidad es mayor y los Focos se desplazan hacia los extremos (F1). Cuando el Rombo se hace más espigado, la excentricidad disminuye y los Focos se acercan al centro (F3). Es decir que cuando el Rombo respira, los Focos (que son móviles) hacen lo mismo: cuando éste se hace pequeño y se achata, los Focos se alejan y cuando el Rombo se hace mayor y se espiga, los Focos se acercan entre sí.
O lo que es lo mismo: cuando los vértices obtusos se juntan, los Focos se separan. Cuando los vértices obtusos se separan, los Focos se acercan.
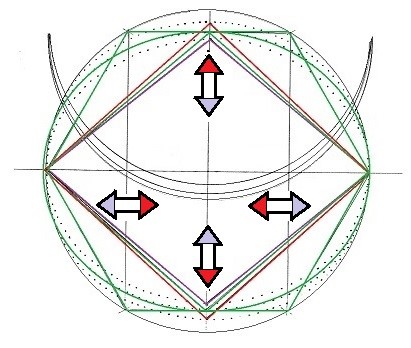
La respiración de la diagonal menor del Rombo y los Focos
Durante el movimiento oscilatorio de la diagonal menor nos aparecen infinitos tipos de Rombos, pero tan sólo uno de ellos forma un hexágono regular. Se trata del Rombo que está aproximadamente a medio camino entre los dos extremos y en el que la diagonal menor por construcción geométrica mide 19.05…..
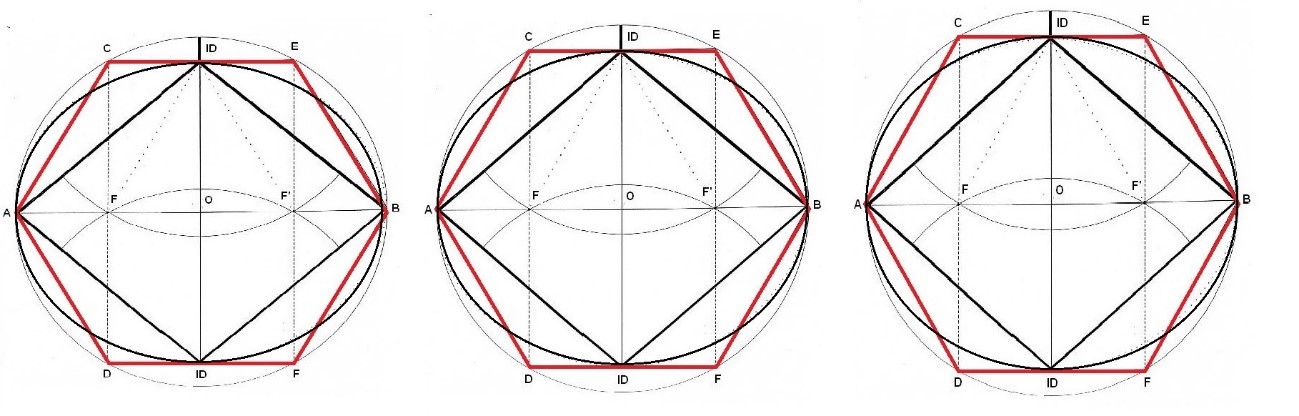
El único hexágono regular está en el centro de la figura
Todos los Rombos son válidos y sólo expresan un momento de la respiración rítmica del Rombo, pero lo cierto es que el único Rombo que forma un hexágono regular y que permite toda la serie de geometría regular es el que tiene una diagonal menor con un valor de 19.05. Por este motivo, este Rombo en concreto ha ocupado en el estudio sobre la geometría del Rombo un lugar tan predominante.
Este Rombo, al igual que los otros, tiene toda una seria de características matemáticas que les son comunes. Una de ellas es la posibilidad de la determinación de la posición de su Foco a partir del tamaño de la Diagonal mayor y la diagonal menor.
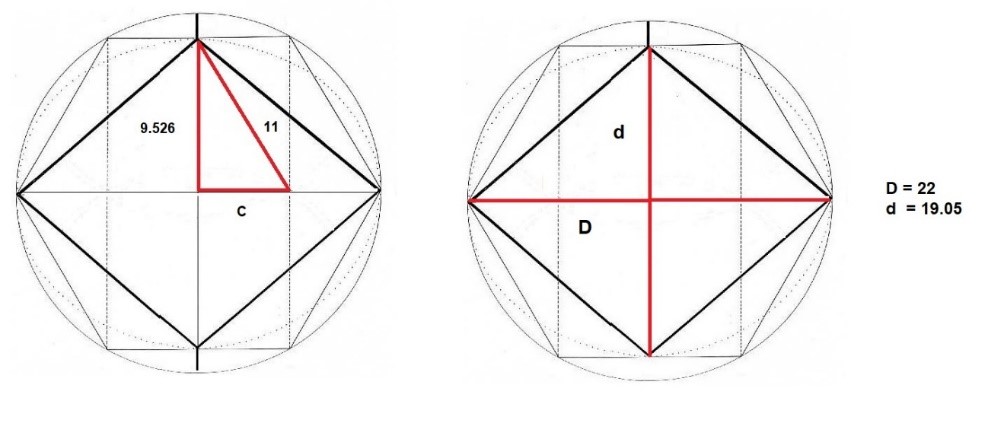
En el dibujo siguiente vemos a la diagonal menor cuyo valor es 2b y a la Diagonal mayor que está designada como 2a. A partir de aquí, observamos que a es el valor que corresponde a la mitad de la Diagonal mayor y también al segmento que va desde el Foco hasta el vértice superior del Rombo.
La distancia que existe entre el centro O y el Foco se llama c. Entonces, podemos calcular el Foco a partir del valor de la semidiagonal mayor y menor.
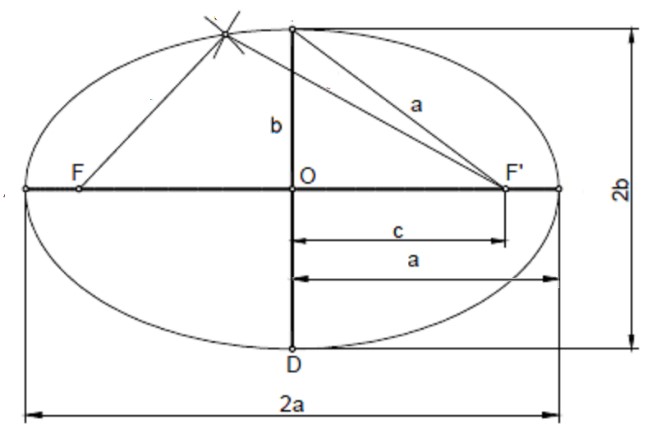
Las distintas partes de la figura
A partir de estos datos previos, y centrándonos en el triángulo que aparece en la parte derecha de la figura podemos estudiar sus razones matemáticas. Si aplicamos Pitágoras, veremos que:
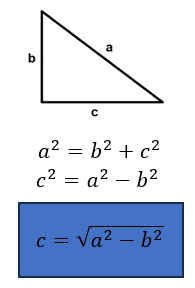
Aplicando esta ecuación en el Rombo anterior, obtendríamos los siguientes valores:
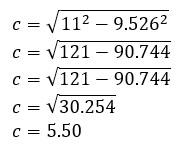
Y si sabemos el valor del Foco podemos calcular la excentricidad de la elipse, que es la razón entre su semidistancia focal (longitud del segmento que parte del centro de la elipse y acaba en uno de sus Focos), y su semieje mayor (Diagonal mayor). El valor de la excentricidad se encuentra entre cero y uno: ( 0≤e ≤1
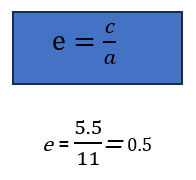
El Rombo con el que hemos trabajado desde el principio (el inscrito en el hexágono regular) tiene muchas características especiales en cuanto a la situación de sus Focos ya que, por construcción geométrica, éstos aparecen espontáneamente al unir las aristas del lado superior e inferior del hexágono.
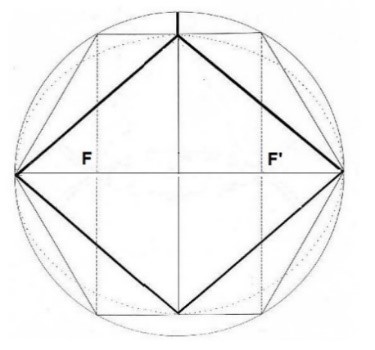
Los Focos aparecen por construcción al unir aristas
Además, observamos que la longitud del radio constructor (11 cm.) que permite dibujar la circunferencia y crear una Diagonal mayor de 22cm, tiene la misma anchura que el lado del hexágono circunscrito y que la distancia F-F´.
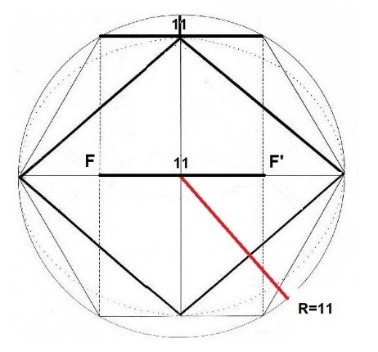
El valor 11 es equivalente para el Radio, el lado del hexágono y la distancia F-F
También podemos ver como la distancia OF o OF´ (5.5 cm.) que se obtiene por construcción es también la mitad del segmento F-F´.
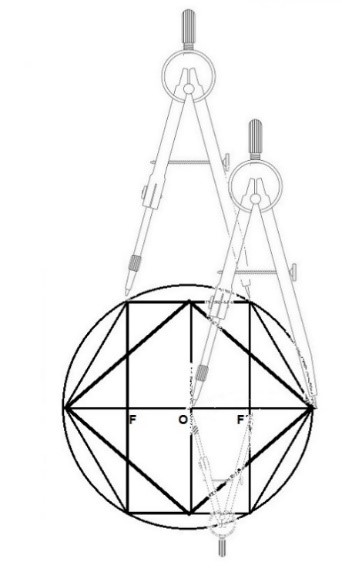
Estos valores se dan por construcción geométrica
Además, si juntamos todos los vértices del hexágono, aparte de los dos Focos principales que se observan en la Diagonal mayor, obtendremos otros 4 Focos más que corresponden a otros Rombos inscritos también dentro de este mismo hexágono pero que permanecen ocultos.
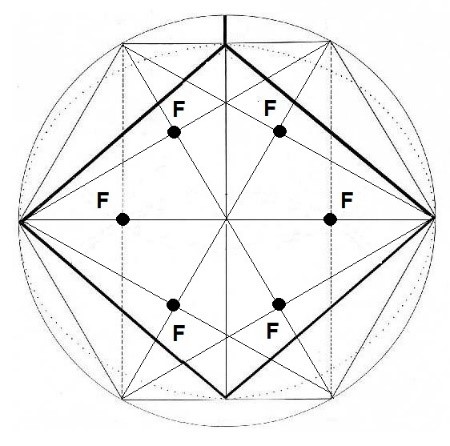
Los Focos aparecen al unir los vértices del hexágono
Y si juntamos los puntos medios de los lados del hexágono, también se obtienen los mismos Focos y además se nos aparece una figura conocida ancestralmente en la que se observan dos triángulos. Uno que apunta hacia el cielo y otro hacia la tierra.
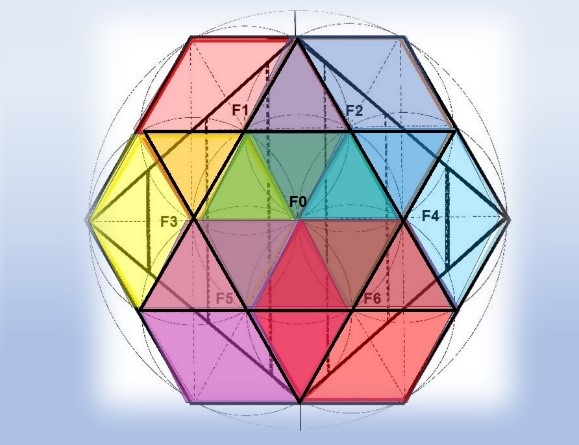
Los F aparecen al unir los puntos medios de los lados alternos del hexágono
Desde cada uno de estos Focos (y con un radio cuyo valor es la mitad del radio matriz) se puede dibujar una circunferencia que al impactar con el Rombo origina una línea vertical que es la que marca el punto de inicio de las dimensiones. Esta figura es conocida como la semilla de la vida.
Además, desde las circunferencias trazadas desde algunas aristas o puntos medios de los lados del hexágono (A, B, C, D, E, F, G, H) podemos hallar los puntos medios de las dimensiones.
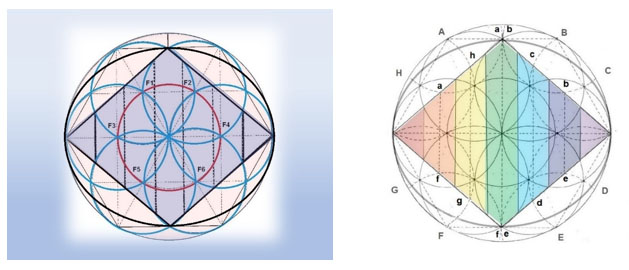
La geometría interna del hexágono regular
Si tenemos en cuenta que el Rombo está en rotación, tomando como guía la rayita superior de Ideación Divina, podemos hacer girar al Rombo hacia la derecha y observar cómo en este giro de 6 pasos, desde el lado superior del hexágono se proyectan dos líneas verticales que van hasta el lado inferior del mismo hexágono y que van tocando puntos de Foco ya conocidos.
En cada paso del giro, se genera un rectángulo que pasa por dos puntos de Foco ya encontrados previamente.
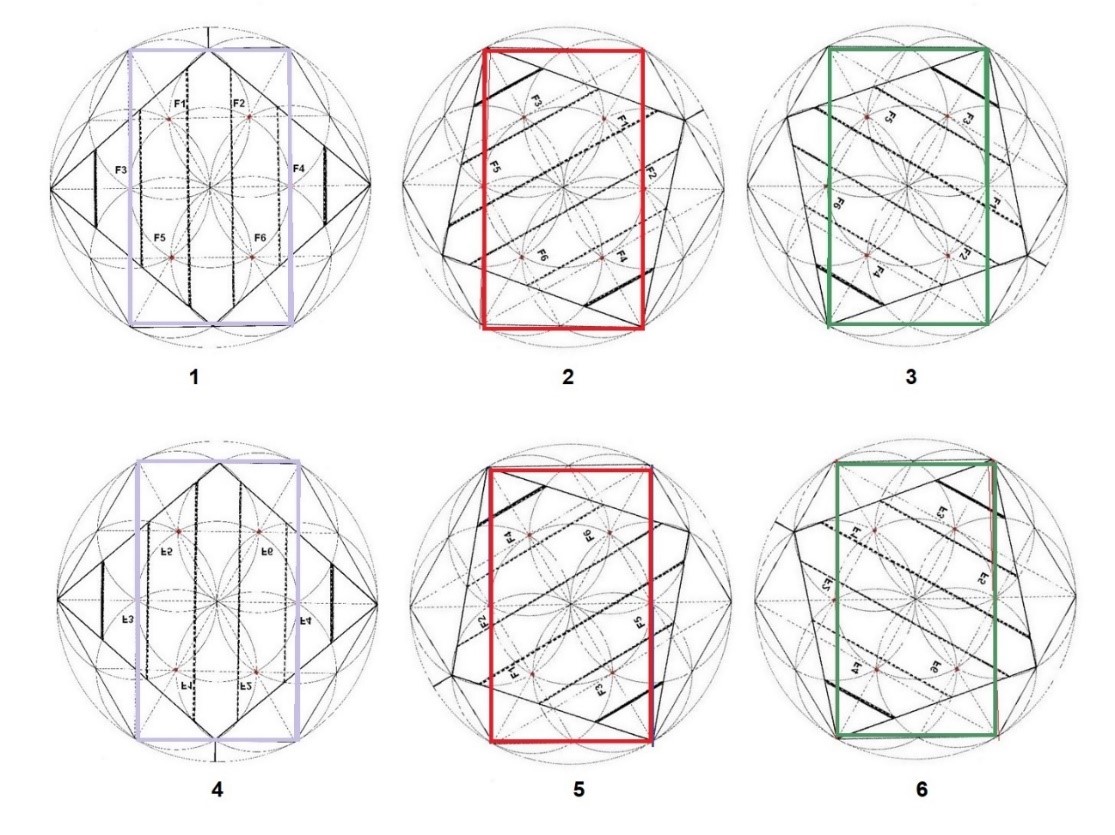
Los 6 pasos de la rotación del Rombo contactan con los puntos de Foco
Al final, observamos que, en los seis pasos de la rotación del Rombo, obtenemos los mismos 6 Focos que habíamos hallado antes.
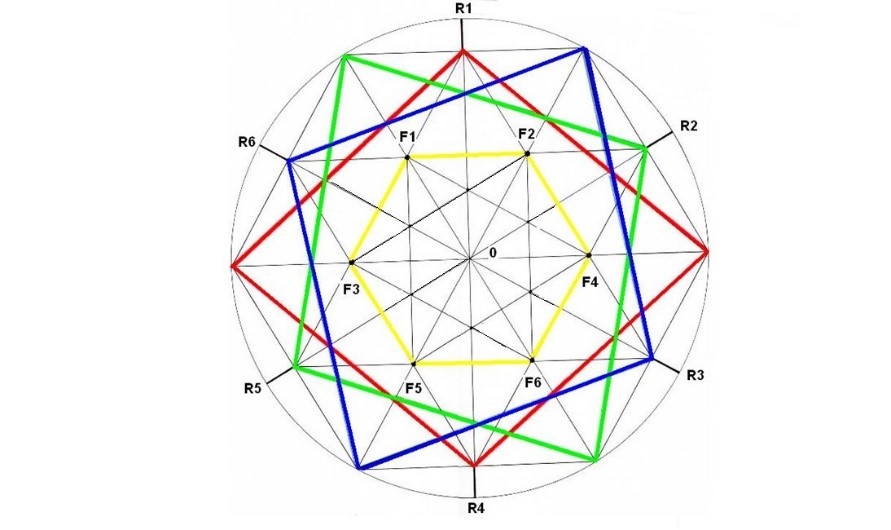
Los 6 Focos obtenidos gracias a la rotación del Rombo
Como que cada Rombo tiene su elipse asociada podemos reunir en un solo dibujo todo el conjunto de las 6 elipses posibles, aunque solamente observemos 3 ya que las demás están superpuestas. Esto produce un dibujo un poco complejo pero que nos enseña cual es la situación real de los Rombos y sus elipses.
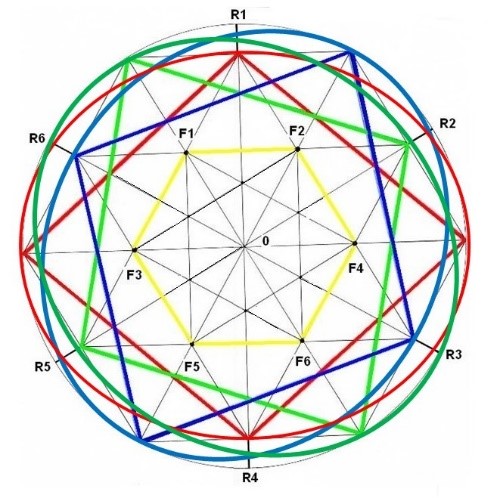
Cada Rombo tiene su elipse asociada
LA ONDA SENOIDAL
La elipse es una figura interesantísima y muy afianzada en el dibujo del Rombo, pero el estudio del movimiento armónico simple que tiene lugar en todo lo manifestado, introdujo una nueva posibilidad de representación de esta línea curva. El dibujo del M.A.S. que es un movimiento oscilatorio universal es equiparable al gráfico que resulta cuando se estudia el movimiento circular uniforme. En este movimiento se genera una línea de tipo senoidal en la que el Rombo también podría quedar perfectamente enmarcado.
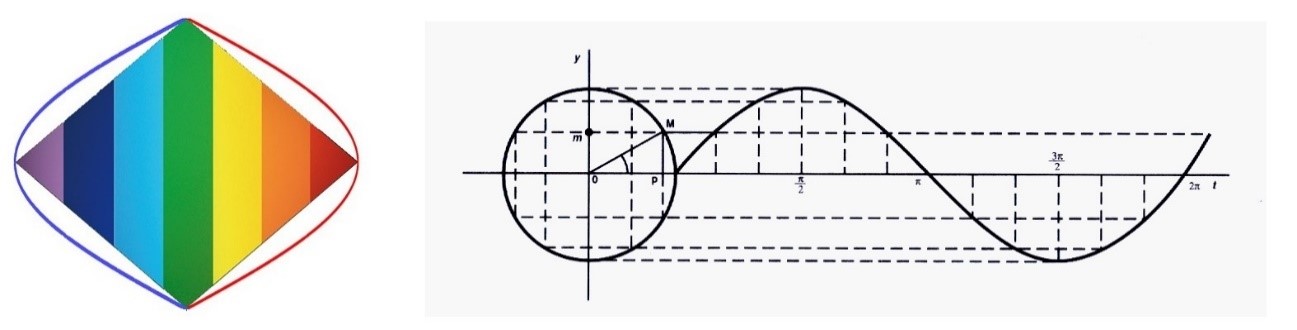
La onda senoidal se crea por el movimiento circular uniforme
Si en vez de estudiar el dibujo que origina un radio en movimiento, se contempla el que produce la Diagonal mayor (dos radios), veremos que se produce una doble curva senoidal en la que podría quedar enmarcada perfectamente la figura del Rombo.
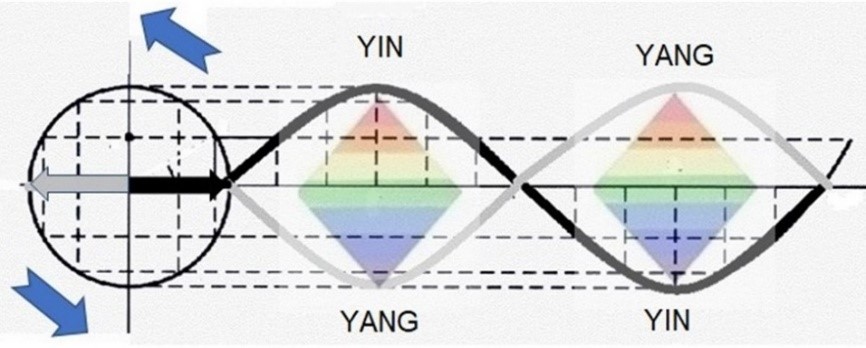
El movimiento circular uniforme crea la curva senoidal
Si en el dibujo ajustamos perfectamente la frecuencia de los ciclos y el tamaño del Rombo, la figura final podría quedar tal como aparece en el dibujo. De manera que obtendríamos un Rombo envuelto por una línea ondulada que no sería ni la circunferencia ni la elipse, sino una onda senoidal.
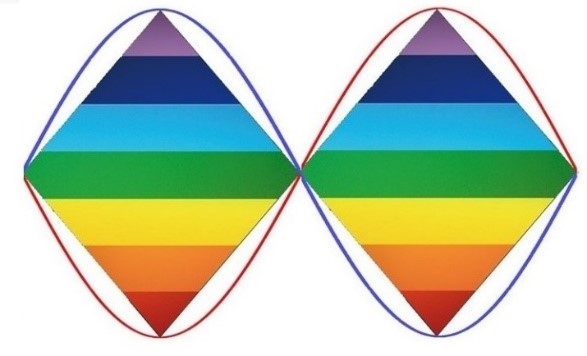
La onda senoidal abraza al Rombo
Esta onda senoidal representaría el resultado de todas las ondas senoidales que se producen dentro del Rombo como resultado de toda su actividad oscilatoria y vibracional.
De esta manera, podrían coexistir sin conflicto dos tipos de ondas asociadas en el Rombo: Una exterior (la elipse) que simbolizaría a las dos fuerzas primigenias Yin-Yang que se introducen en el Rombo para crear la posibilidad de que se produzca vida palpitante y una más interior (la onda senoidal) que sería la representación de toda la actividad vibracional que se está generando por la oscilación de la misma vida.

Las dos curvas asociadas al Rombo
Con este acuerdo conceptual cerramos en su día uno de los debates más interesantes que hubo sobre las diferentes ondas que podían existir fuera del Rombo. Las dos líneas onduladas no eran incompatibles entre sí. Ambas tenían cabida y expresaban conceptos diferentes.
LA VESICA PISCIS
El hecho de que en el dibujo inicial del Rombo se contemplara la posibilidad de que existieran dos semicircunferencias unidas, hacía recordar a lo que le sucedía a la circunferencia primigenia (que representaba a la Unidad) cuando daba paso a la dualidad y se convertía así en la figura conocida como la “vésica piscis”.

La dualidad representada por la vésica piscis
Esta figura se asociaba de alguna manera con el Rombo, en el que existían también dos polaridades diferenciadas. Además, en el dibujo fusionado de la vésica piscis y el Rombo se daban algunas circunstancias curiosas; cada una de las dos circunferencias grises tenía su centro en un Foco del Rombo, y en su trayecto contactaba con las puntas de los vértices obtusos que tocan a I.D., con la transición de 3ª- 4ª o 4ª- 5ªdimensión y con el Foco de la otra circunferencia.
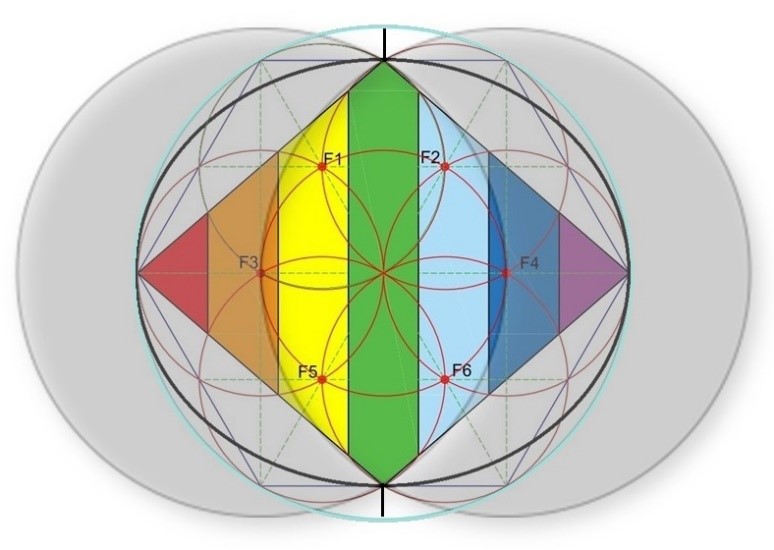
Relación geométrica e interdependencia entre la vésica piscis y el Rombo
Si a esta figura la hacíamos girar, podíamos ver que a pesar de la rotación en 6 pasos de la vésica piscis, el dibujo de la margarita central con sus Focos se mantenía en el mismo lugar.
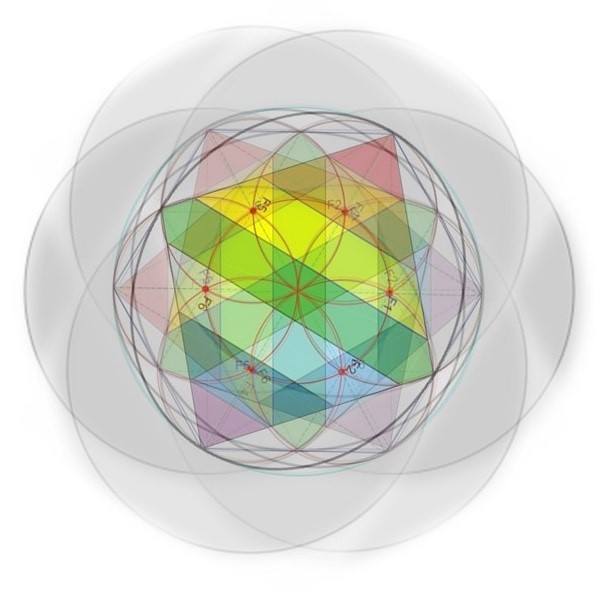
La vésica piscis ha rotado y se mantienen constantes los Focos y la margarita
Si analizamos otros detalles del dibujo conjunto de la vésica piscis y el Rombo podemos observar que en la línea horizontal se dibujan 6 espacios con un tamaño de Foco mientras que en la vertical se dibujan 4 espacios de Foco.
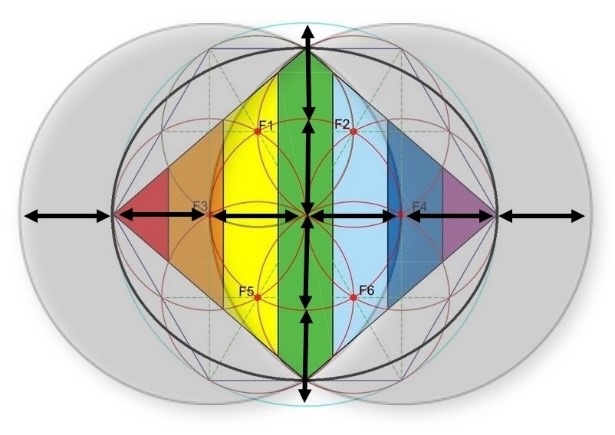
Las peculiaridades de la vésica piscis y el Rombo
Hace tiempo, cuando empezamos a hacer los primeros dibujos del Rombo y no sabíamos (conscientemente) nada de lo que se conoce como geometría sagrada, realizamos muchos dibujos exploratorios y éste de las tres margaritas fue uno de aquellos primeros diseños. En él se observa la vésica piscis, una circunferencia central adicional con un hexágono y su Rombo. Además, se puede ver una margarita central acompañada de margaritas laterales.
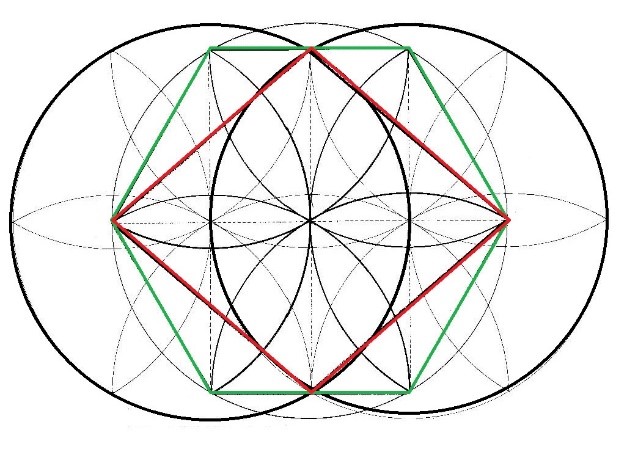
Tres circunferencias con sus margaritas
Si ahora al Rombo que está ubicado en el centro le superponemos el Rombo de colores con sus Focos, obtenemos una figura en la que vemos a una margarita central pequeña que es la mitad de la margarita encuadrada dentro del hexágono.
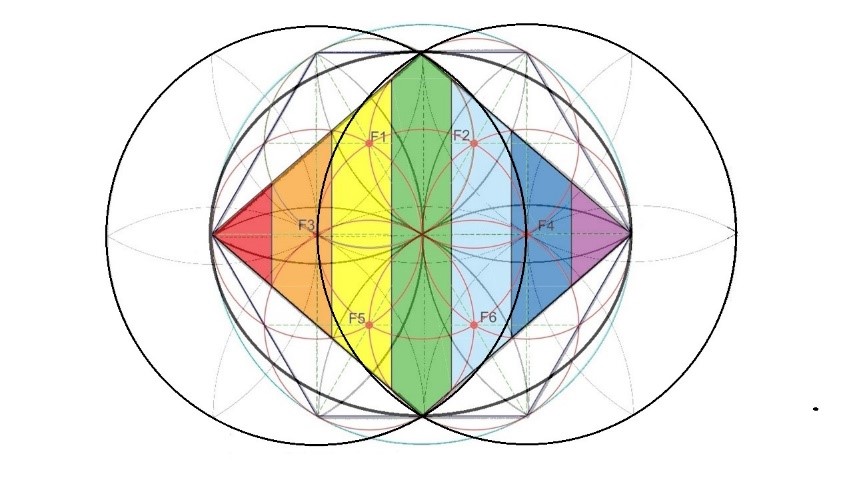
El dibujo anterior con el Rombo nuevo
Si lo queremos desarrollar un poco más, podemos dibujar los tres Rombos que caben en la figura. Al hacerlo, observamos algunas curiosidades. Por ejemplo, podemos ver que:
- El centro de cada uno de los Rombos situados en los extremos coincide con uno de los vértices agudos del Rombo del extremo opuesto, con su elipse asociada y con la línea curva de la vésica piscis.
- El centro del Rombo que está ubicado en la posición medial se superpone con un Foco de cada uno de los Rombos ubicados en los extremos.
- Los ángulos agudos del Rombo central coinciden con Focos de los Rombos de los extremos.
- Los dos vértices obtusos del Rombo central contactan con la intersección de las dos circunferencias.
- Se originan tres margaritas pequeñas alineadas en la Diagonal mayor.
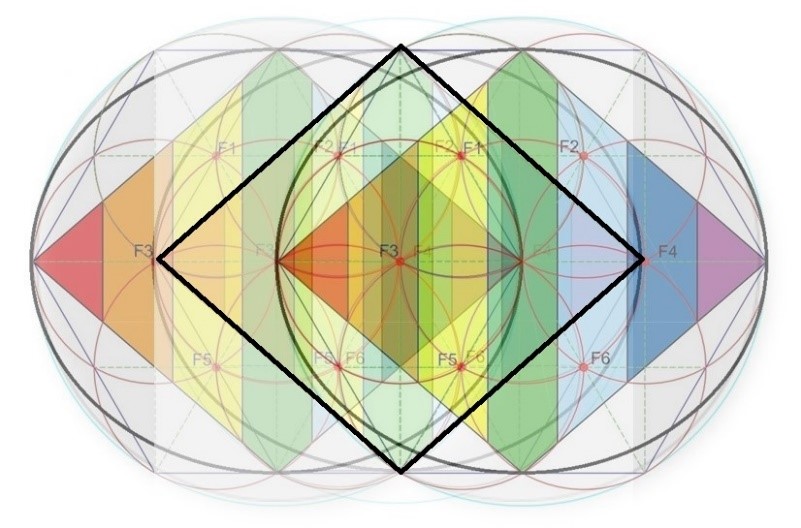
En la vésica piscis confluyen tres Rombos
Con todo esto, podemos constatar que hay una relación muy compleja entre los centros, los Focos y los ángulos agudos de los Rombos:
- Se puede ver que el centro de las circunferencias exteriores (punto Hara) recibe la energía creadora del vértice agudo correspondiente a la 1ª o 7ª dimensión del Rombo del otro extremo, por lo que es lógico comprender el poder creador que tiene el centro.
- Además, vemos que los Focos distales de los Rombos exteriores situados en la Diagonal mayor, están en contacto con la 1ª o 7ª dimensión del Rombo central, lo que les otorga una gran fuerza de creación.
- El punto central de cada margarita recibe también la energía que viene de los vértices obtusos superior e inferior en su trayecto a través de la diagonal menor.
- El punto central de margarita interacciona con los 6 Focos de su alrededor.
- Los puntos centrales de las margaritas se comunican con las otras a través de la Diagonal mayor.
Todos estos detalles permiten entender la fuerza creadora de los Focos, el centro, los vértices agudos y los obtusos pues todos están ellos están interconectados en múltiples circuitos.
Además, si miramos con un poco de detalle el siguiente dibujo del Rombo con las 6 circunferencias que están relacionadas con su estructura interna, veremos que no hay sólo una vésica piscis, sino unas cuantas más.
Podemos observar 6 vésica piscis que siguen un trayecto exterior y que reúnen a las 6 circunferencias vecinas. Y además también se pueden ver a las 6 vésica piscis que aparecen entre cada una de las circunferencias exteriores y la circunferencia central. En total son 12.
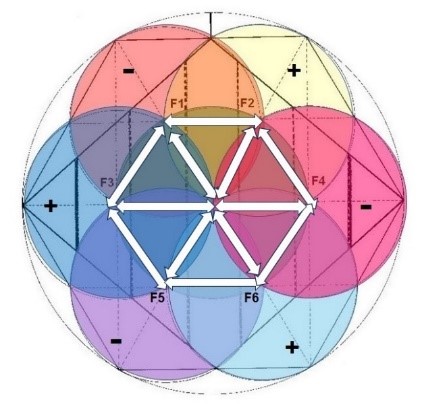
12 vésica piscis
Y lo que se desprende de este dibujo es que entre cada dos circunferencias vecinas que crean una vésica piscis, se crea un Rombo completo.
Al final sucede que se pueden crear 12 Rombos pequeños a partir de un Rombo madre y que cada uno de ellos crea otros 12 indefinidamente.
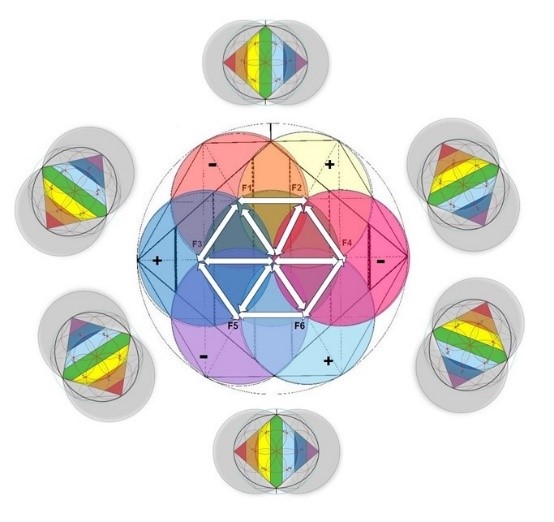
12 Rombos dentro de un Rombo. 6 en el exterior y 6 más en el interior
(estos últimos no están representados)
De esta manera, y aunque el estudio de la vésica piscis fue muy posterior a la aparición del dibujo de las dos semicircunferencias del Rombo y a la elipse, su estudio vino a aportar muchos datos acerca de la simetría interna del Rombo, de su construcción y de la intercomunicación de los Focos con otras partes del Rombo.
LA ELIPSE TRIDIMENSIONAL
Si alzamos la vista y miramos con ojos tridimensionales al Rombo, entenderemos que no es realmente una elipse lo que le rodea, sino una pseudoesfera elíptica tridimensional. Y tampoco es una onda senoidal plana lo que lo abraza, sino que se trata de una onda senoidal tridimensional. La elipse y la onda senoidal tal como las hemos dibujado, sólo son proyecciones en dos dimensiones de esa realidad superior, de la misma manera que el Rombo bidimensional es la proyección del Rombo tridimensional.
Al pasar la elipse del mundo bidimensional al tridimensional, parece que las cosas cambian, pero realmente es el mismo objeto representado en una dimensión diferente. Esta forma elíptica tridimensional que envuelve y arropa al Rombo tiene dos polaridades diferenciadas: Yin y Yang.
Esta esfera elíptica (que se asemeja a un huevo cósmico) nutre al Rombo con estas dos energías creadoras que fluyen continuamente la una hacia la otra y que interaccionan en todos los puntos del Rombo, pero que convergen de una forma muy especial en el centro, en una zona en donde la fusión y el equilibrio de estas dos polaridades es máximo.
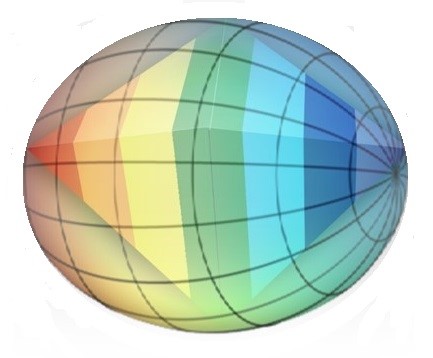
La pseudoesfera elíptica tridimensional que envuelve al Rombo
Si miramos la figura en dos dimensiones, podemos pensar que Yin y Yang sólo pueden entrar por los vértices que contactan con la elipse, pero si observamos la figura de la pseudoesfera elíptica podemos pensar que la fuerza Yin-Yang es como una nube que envuelve al universo manifestado y que por lo tanto estas dos fuerzas creadoras pueden entrar por cualquier lugar, ya que, en cualquier zona o punto del Rombo, coexisten la 1ª y la 7ª dimensión.
Es cierto que en el esquema básico hay una gran 1ª-7ª dimensión, pero por holografía, podemos entender que hay miles de pequeñas puertas de entrada Yin-Yang en todo el Rombo. Este concepto quedó reflejado hace ya mucho tiempo en un dibujo conocido como el Rombo de Rombos.
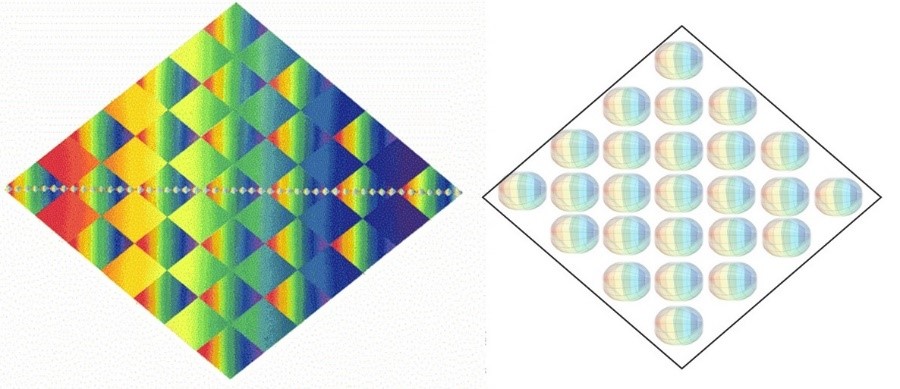
La elipse tridimensional holográfica
En el Rombo todo es simbólico y la información se encuentra escrita en un lenguaje geométrico y numérico muy esquemático. Pero detrás de esa aparente simplicidad aparece un mundo rico y complejo, donde de una manera sorprendente, cada vez los dibujos que inicialmente dentro de la geometría sagrada parecían estar separados entre si (la circunferencia, la elipse, el hexágono, el Rombo, la semilla de la vida, la estrella de David o la vésica piscis) empiezan a converger, a fusionarse y a dejar entrever la interconexión geométrica que existe en todo lo creado.