El Rombo tridimensional (1ª parte)

Introducción

Dicen que la figura bidimensional es más complicada que la tridimensional, porque en dos dimensiones, se deben plasmar tres y todo ha de pasar por un proceso de compresión que obliga a un ejercicio mental continuo para entender en dos dimensiones lo que ocurre en tres.

La segunda dimensión parece estar llena de efectos ópticos que te hacen percibir unas cosas que no existen y en cambio, te hace desaparecer de la vista, otros fenómenos que son muy evidentes.

Además, la figura dimensional, sólo es la expresión momentánea de un ángulo de rotación concreto de la figura en tres dimensiones. Por todo esto, resulta compleja, difícil de entender y puede llevar a confusiones.

Cuando, en cambio, utilizas la tercera dimensión, ves que la geometría es distinta y te parece muy difícil que en un dibujo bidimensional se pueda reflejar lo que realmente tiene lugar en el mundo tridimensional. Sucede que, aunque se pueda hacer una proyección, algunas líneas coinciden con otras, las tapan, las hacen desaparecer o dotar de un movimiento en el espacio que no tienen. Cuando estás en la tercera dimensión, ves que todo es mucho más libre y movible, lo que pensabas que era cierto, resulta que no lo es, y aquello que no existía, de repente, aparece de la nada. Por otro lado, resulta muy difícil localizar en tres dimensiones los dibujos geométricos que se han hecho en dos dimensiones. No sabes si esa circunferencia interior con la que estabas tan familiarizado está delante o detrás, y aquellas margaritas que tan preciosas, parecían adornar de vida una figura rectilínea, pierden su ubicación y no ves si se sitúan superficialmente o en profundidad. Da la sensación de que todo lo que habías visto, ahora, cuelga ingrávido en el aire, flotando, sin saber donde ir para poder descansar en geométrica paz. En un suspiro, te han quitado todo lo que tenías y te dan algo nuevo, vacío y con la vibrante necesidad de ser llenado. Te ha desaparecido el juguete de la infancia, el que habías volteado una y otra vez, y ahora, ves que debes jugar a algo distinto, pero no sabes exactamente como.

Me acuerdo de un artículo que escribí sobre la cuarta dimensión, inspirado en el cuento de Abbot que decía lo difícil que le sería a un ser bidimensional, el poder imaginar una tercera dimensión. En el artículo, se decía que si, por ejemplo, un ser tridimensional, entrara en la 2ª D, un habitante de Planilandia, sólo podría ver los puntos de contacto de la 2ª D con la 3ª D. Diría que los hombres de la 3ª D son dos manchas, asociadas a una voz que procede de todos los sitios.

Algo similar ocurre en el Rombo 2D y cuando lo ves en 3D, te das cuenta que todo lo que has pensado en 2D, es una apreciación parcial y susceptible de ser revisada. Estamos habituados a trabajar en dos dimensiones y parece que hay cierta dificultad inicial en ponerse a trabajar con figuras tridimensionales ya que exige una apertura del pensamiento, un desarrollo de la geometría espacial, y un aumento de la profundidad de la visión.

Siempre se nos ha recalcado la necesidad de hacer manualidades, pero este mensaje, tan repetido, ha quedado a menudo, relegado a una idea conceptual, depositada en el mar de las ideas. Así que para romper esta inercia aferrante bidimensional, y para aventurarme un poco en un mundo más libre, decidí hacer un trabajo partiendo de lo que había descubierto en el mundo bidimensional, y darle una realidad en una dimensión superior.

Iba a realizar una sencilla manualidad tridimensional. Tengo que decir que, de este ensayo artístico, nació una estructura totalmente distinta de la que quería hacer. Se ve que esto, forma parte de mi manera de iniciar. Casi siempre, cuando empiezo algo, me equivoco, creo una cosa distinta a la que buscaba y no encuentro lo que deseo, pero luego, para endulzar la amargura del error, y para mi sorpresa, resulta que el error está lleno de posibilidades y abre nuevas vías de pensamiento. En el caso concreto de esta manualidad, también me sucedió lo mismo, pero … prefiero no adelantarme. Empezaré por el inicio.

La idea de la búsqueda tridimensional del Rombo, partió del prisma hexagonal en el que suponía que estaba anclado el Rombo.

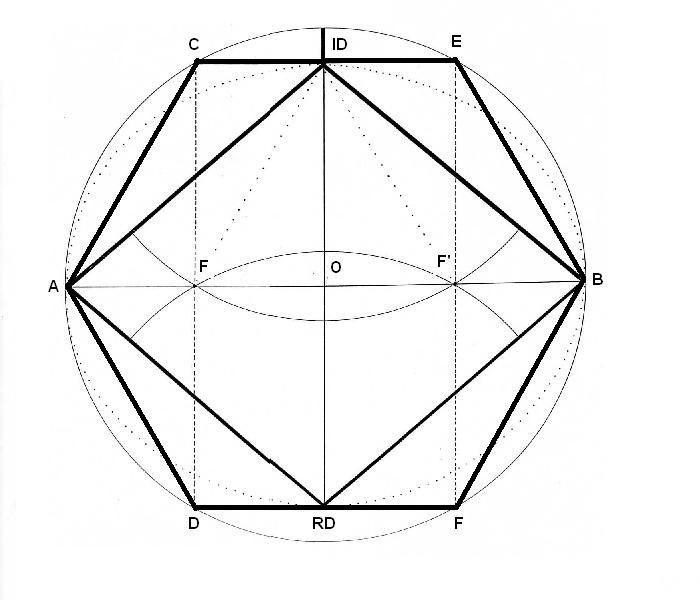
El Rombo dentro del prisma hexagonal

Así que, sin dudar, me armé de esferas de corcho, palillos de madera y empecé a desplegar el ingenio artístico. Pero cuando lo estaba montando, vi que la primera figura que me salía, no se ajustaba a lo el esperado. Yo esperaba un Rombo en proyección frontal, pero no en proyección lateral. Esperaba la figura de arriba, pero me encontré con las de abajo.

Todo fueron sorpresas

En ese instante, comprobé que acababa de demostrar de una manera palpable una sospecha que había intuido desde mi tierna infancia: ¡No me iba a dedicar a las artes plásticas!

Me había encontrado con esa sorpresa, y vi que tenía delante, más o menos lo que quería, que no era nada más y nada menos que el armazón del Rombo tridimensional. Cierto es que era una visión lateral, pero en ese momento, no importaba mucho. Había aparecido una estructura de soporte. Distinta a la esperada, (no lo puedo negar), pero también era real, y para algo podría ser utilizada.

Este prototipo, ya me podría servir para lo que quería hacer, que era iniciar cálculos matemáticos para determinar los valores que tendría el Rombo para los dos conceptos que habíamos manejado durante mucho tiempo. Eran dos palabras que teníamos tan asumidas como poco desarrolladas: Rombo 22 interior y Rombo 22 exterior.

Siempre habíamos hablado de ellos, pero nunca habíamos tenido la curiosidad de ver en que consistían realmente. Como que ya hace tiempo, me he dado cuenta que en este florido jardín, no crece nada que no haya sido plantado, pensé que quizás ya era hora de poner la primera semilla y ver que sucedía si la regábamos un poco.

Este artículo, intentará explicar a qué resultados geométricos elementales se llegó y que consideraciones se pueden desprender. Como veremos, los resultados del estudio abrirán muchas puertas y generarán muchas más dudas, haciendo palpable la idea general de que este juego, no tiene fin. Empecemos….

22 INTERIOR

Rombo 22 interior. El vértice violeta y el rojo están unidos por una línea que corre por el centro de la figura y que sigue el eje de los planos de conciencia.

Para entrar en el análisis del Rombo 22 exterior e interior, nos ayudará la figura que está un poco más abajo. Se trata de una lámina que apareció cuando hablábamos del 18-19. En este dibujo, queríamos plasmar como se ve el Rombo desde la 1ª o 7ª D. Visto desde estos vértices, la figura, haciendo un alarde de efectismo, parece un triángulo equilátero. En este caso, se representaron los dos triángulos, pero para lo que vamos a llevar a cabo, nos bastará con mirar el triángulo amarillo.

En concreto, estamos interesados en saber lo que mide la raya roja, que es un trocito de la mediana.

La verdad es que, sólo fijándonos un poco, veremos que la línea roja es la mitad exacta de la línea que va desde el centro al vértice C. Sabiendo que OC mide 11 cm., está claro que la línea roja, por construcción, mide 5.5 cm., lo cual será muy interesante para lo que vamos a llevar a cabo.

Si quisiéramos calcular matemáticamente esta cifra, deberíamos acudir a Pitágoras y aplicar la fórmula para el triángulo rojo. Conocemos dos lados y debemos hallar el tercero. (Suponemos 5.5)

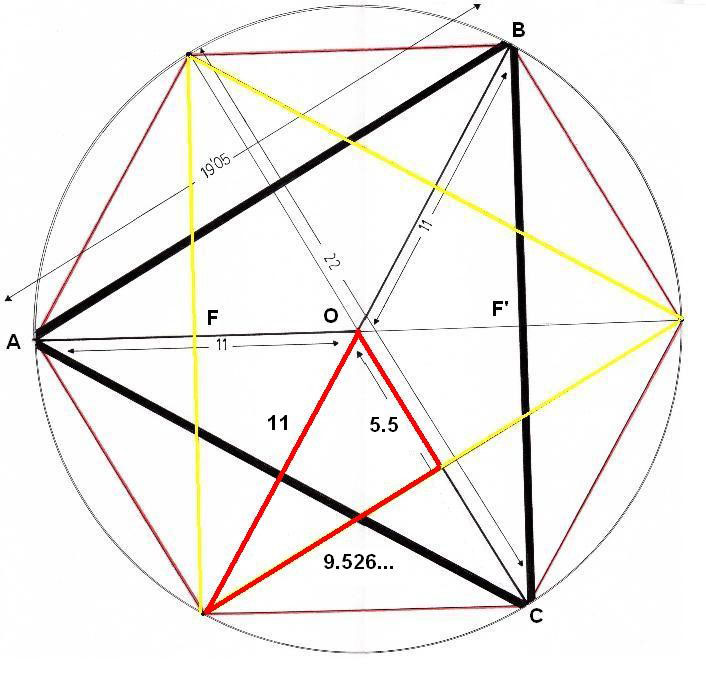
Dibujo de la serie 18-19

                            C² = H² - C²

                                      ____________
                             C = √ 11 ² - 9.526 ²

                                      _________
                             C = √30.255324

                                       

                              C = 5.50

Con esto, obtenemos un valor muy interesante, que ya conocíamos. Esta operación pitagórica, la podemos hacer en todos los triángulos en los que 11 ( la mitad de la DM ) es un valor constante y en el que solo varia 9.526 ( que es la mitad de la dm) . Para ir un poco más rápidos, buscaremos una fórmula ya conocida.

L            H =   ______                          __                     2 √3

Esta es la fórmula base que nos permitirá desarrollar más rápidamente todo el cálculo posterior. Su presencia no tiene más valor que el de poder hacer las operaciones con más celeridad, pero podemos emplear el sistema tradicional. No tiene mayor importancia.

Construcciones tridimensionales

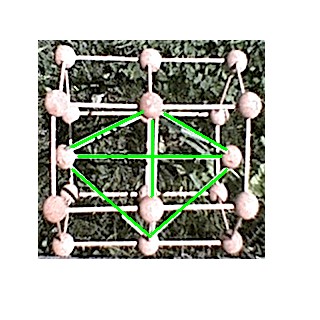
Miremos ahora el triángulo verde del Rombo. Observamos al triángulo y vemos como uno de sus vértices apunta a la izquierda. Desde allí, sale una arista hacia el centro de la figura, donde se halla la esfera central. Vemos que desde esta esfera hacia la derecha no hay nada. Ese espacio precisamente es el que hemos determinado y el que nos ayudará a realizar todos los cálculos para el tamaño del Rombo.

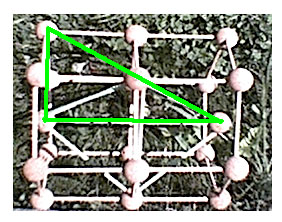
En la foto de la derecha, el Rombo apoyado, marca el triángulo superior, que será objeto de todo el estudio. Bueno, todo parece dispuesto. Podemos empezar con los números.

PRIMER SISTEMA DE CÁLCULO PARA DETERMINAR LA
APOTEMA EXTERIOR PARA 22 FIJO INTERIOR

Para entender mejor las cosas, deberemos acudir a otra fotografía. Aquí vemos al Rombo de lado, dentro del prisma hexagonal, apoyado en un equilibrio inestable sobre uno de sus vértices (gracias a la hierba)

Un vértice del hexágono toca el suelo. Como que es un poco difícil de ver, haremos una representación bidimensional de lo que queremos estudiar y trasladaremos a dos dimensiones lo que aparece en la foto. Conocemos dos catetos y nos falta hallar la hipotenusa.

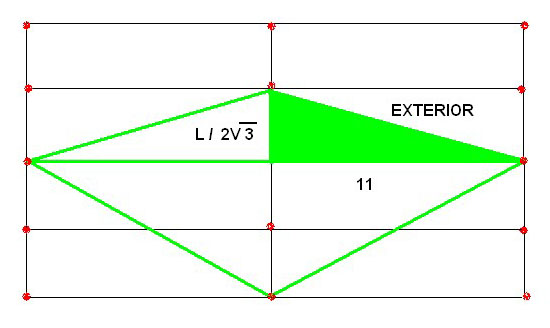
El Rombo tridimensional visto cuando uno de sus vértices está apoyado en el

suelo. El concepto “exterior” es la apotema y no los lados.

Haremos un ejemplo. Deseamos calcular cual es el tamaño exterior de un Rombo de 18 cm. de diagonal menor y de 22 cm interior.

                       __________________
Exterior = √ (18 / 2√3) ² + (11)²

                       _____________
Exterior =   √ 324/ 12 + 121

                     _____
Exterior = √ 148

Exterior = 12.16552506.

Como que el tamaño del Rombo son el exterior ascendente y el descendente, deberemos multiplicar esta cifra por dos, con lo que tendremos que:

Exterior total del Rombo = 24.331

Para determinar todos los otros valores posibles, iremos aplicando la misma fórmula. El único valor que irá variando será el del lado del triángulo que queramos estudiar

SEGUNDO SISTEMA DE CÁLCULO PARA DETERMINAR LA
APOTEMA EXTERIOR PARA 22 FIJO INTERIOR

Por sino teníamos bastante con un sistema de cálculo, buscaremos otro. Estoy seguro que como mínimo habrán media docena de formas de hallar lo que estamos buscando, pero estas dos, de momento, ya me han parecido suficientes. Bien. Utilizaremos primero la foto del Rombo tridimensional para situarnos.

En este segundo caso, que es muy parecido al anterior, utilizaremos el triángulo mayor. Es lo mismo calcular la parte exterior ascendente y luego multiplicarla por dos que hacerlo directamente con triángulo cuyo exterior ya mide el doble. En este caso, los catetos miden también por construcción y por cálculo el doble que en la otra figura.

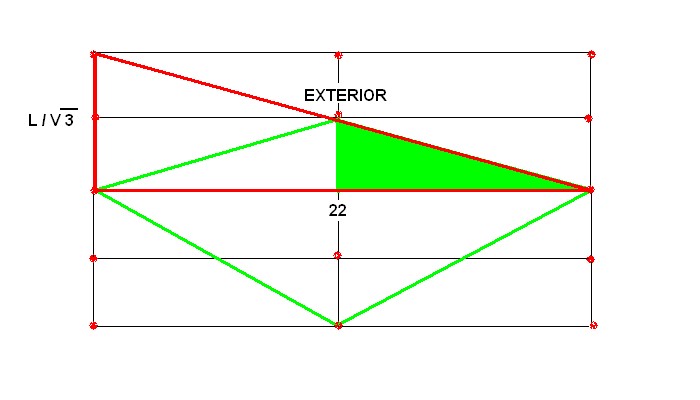
Dibujo del Rombo tridimensional con un vértice apoyado en el suelo.

Se trata más de un triángulo imaginario que real, pero para efectos de cálculo, tiene la misma utilidad. Calcularemos también el tamaño exterior de un Rombo cuya dimensión menor es de 18 cm.

           ______________
E = √ (L / √3)² + 22 ²

         ______________
E = √ (18 / √3)² + 484

           __________
E = √ 108 + 484

           ___
E = √592

Exterior total del Rombo = 24. 331

                          

El resultado como vemos es el mismo que en el anterior cálculo. Podemos hacer los cálculos comparativos con los dos sistemas y lógicamente, los valores encontrados son los mismos.

Bien, hacemos los cálculos y los exponemos en la tabla de medidas exteriores para 22 interior fijo. Veremos que los valores exteriores van variando según el tamaño de la diagonal menor del Rombo. A la izquierda aparece el valor de la diagonal menor y a la derecha, el valor de la apotema, que es lo que llamamos exterior.

TABLA DE MEDIDAS EXTERIORES (PARA 22 FIJO INTERIOR)

 

18.00	24.331		18.50	24.455		19.00	24.583		19.50	24.713
18.01	24.333		18.51	24.458		19.01	24.585		19.51	24.715
18.02	24.335		18.52	24.460		19.02	24.588		19.52	24.718
18.03	24.338		18.53	24.463		19.03	24.590		19.53	24.721
18.04	24.340		18.54	24.465		19.04	24.593		19.54	24.723
18.05	24.343		18.55	24.468		19.05	24.596		19.55	24.726
18.06	24.345		18.56	24.470		19.06	24.598		19.56	24.729
18.07	24.348		18.57	24.473		19.07	24.601		19.57	24.731
18.08	24.350		18.58	24.475		19.08	24.603		19.58	24.734
18.09	24.353		18.59	24.478		19.09	24.606		19.59	24.737
18.10	24.355		18.60	24.481		19.10	24.609		19.60	24.739
18.11	24.358		18.61	24.483		19.11	24.611		19.61	24.742
18.12	24.360		18.62	24.486		19.12	24.614		19.62	24.744
18.13	24.363		18.63	24.488		19.13	24.616		19.63	24.747
18.14	24.365		18.64	24.491		19.14	24.619		19.64	24.750
18.15	24.368		18.65	24.493		19.15	24.621		19.65	24.752
18.16	24.370		18.66	24.496		19.16	24.624		19.66	24.755
18.17	24.373		18.67	24.498		19.17	24.627		19.67	24.758
18.18	24.375		18.68	24.501		19.18	24.629		19.68	24.760
18.19	24.378		18.69	24.503		19.19	24.632		19.69	24.763
18.20	24.380		18.70	24.506		19.20	24.634		19.70	24.766
18.21	24.383		18.71	24.508		19.21	24.637		19.71	24.768
18.22	24.385		18.72	24.511		19.22	24.640		19.72	24.771
18.23	24.388		18.73	24.514		19.23	24.642		19.73	24.774
18.24	24.390		18.74	24.516		19.24	24.645		19.74	24.776
18.25	24.393		18.75	24.519		19.25	24.647		19.75	24.779
18.26	24.395		18.76	24.521		19.26	24.650		19.76	24.782
18.27	24.398		18.77	24.524		19.27	24.653		19.77	24.784
18.28	24.400		18.78	24.526		19.28	24.655		19.78	24.787
18.29	24.403		18.79	24.529		19.29	24.658		19.79	24.790
18.30	24.405		18.80	24.531		19.30	24.660		19.80	24.792
18.31	24.408		18.81	24.534		19.31	24.663		19.81	24.795
18.32	24.410		18.82	24.536		19.32	24.666		19.82	24.798
18.33	24.413		18.83	24.539		19.33	24.668		19.83	24.800
18.34	24.415		18.84	24.542		19.34	24.671		19.84	24.803
18.35	24.418		18.85	24.544		19.35	24.674		19.85	24.806
18.36	24.420		18.86	24.547		19.36	24.676		19.86	24.808
18.37	24.423		18.87	24.549		19.37	24.679		19.87	24.811
18.38	24.425		18.88	24.552		19.38	24.681		19.88	24.814
18.39	24.428		18.89	24.554		19.39	24.684		19.89	24.816
18.40	24.430		18.90	24.557		19.40	24.687		19.90	24.819
18.41	24.433		18.91	24.560		19.41	24.689		19.91	24.822
18.42	24.435		18.92	24.562		19.42	24.692		19.92	24.824
18.43	24.438		18.93	24.565		19.43	24.694		19.93	24.827
18.44	24.440		18.94	24.567		19.44	24.697		19.94	24.830
18.45	24.443		18.95	24.570		19.45	24.700		19.95	24.832
18.46	24.445		18.96	24.572		19.46	24.702		19.96	24.835
18.47	24.448		18.97	24.575		19.47	24.705		19.97	24.838
18.48	24.450		18.98	24.578		19.48	24.708		19.98	24.840
18.49	24.453		18.99	24.580		19.49	24.710		19.99	24.843

Lo que observamos es que siendo 22 interior fijo, a medida que la diagonal menor va aumentando, se va haciendo mayor el valor de la apotema exterior.

Sabemos que cuando la diagonal menor, tiene cifras altas, se relaciona con el ángulo rojo del arco iris, y cuando la diagonal menor tiene valores pequeños, está vinculada al color violeta del arco iris. Lo representamos en el dibujo.

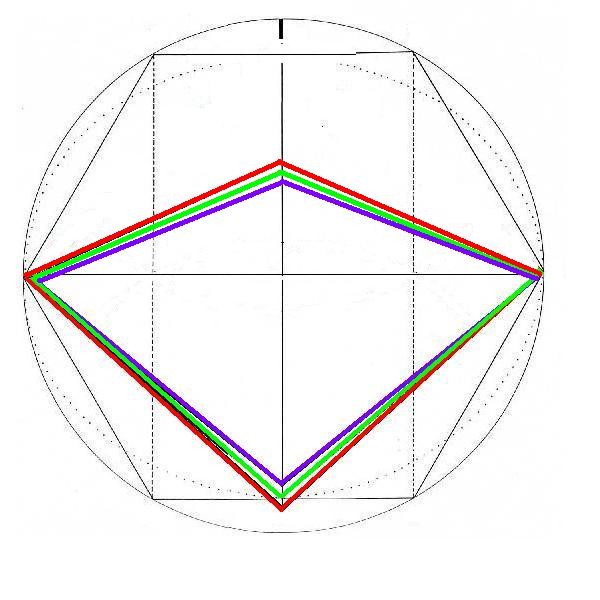
El Rombo rotado 45º para visualizar la apotema

El tamaño de la apotema, o exterior, se va haciendo mayor en la medida en que la línea ha de ir más hacia arriba y recorrer, por tanto, más trayecto. La línea roja es más larga que la violeta porque su trayecto es más largo. Es comprensible que, para 22 interior fijo, a medida que aumenta la diagonal menor, aumente la apotema.

Según se desprende de la tabla, tenemos que para 22 interior fijo y partiendo de una diagonal menor de 18, obtenemos una apotema de 24.331 y para una diagonal menor de 19.99, hallamos una apotema de 24.843. Es decir, que sólo existe una diferencia de 0.512 cm. Con lo que vemos que la oscilación del Rombo (18-19.99) provoca un cambio mínimo del tamaño del Rombo exterior.

22 EXTERIOR

Imagen del Rombo 22 exterior

Bien, ahora vamos a estudiar la otra posibilidad. Se trata del Rombo con 22 fijo exterior. En este caso, el tamaño exterior es fijo. Seguimos teniendo la diagonal menor que tiene su oscilación (18-19.99). De ello, resultará que la Diagonal Mayor será móvil también y tendrá un valor, que dependerá de los distintos valores de la diagonal menor. Hemos de determinar los valores interiores de los Rombos causados por la oscilación de la diagonal menor. Igual que antes, dispondremos de dos sistemas para hacerlo:

PRIMER SISTEMA DE CALCULO PARA MEDIDAS INTERIORES

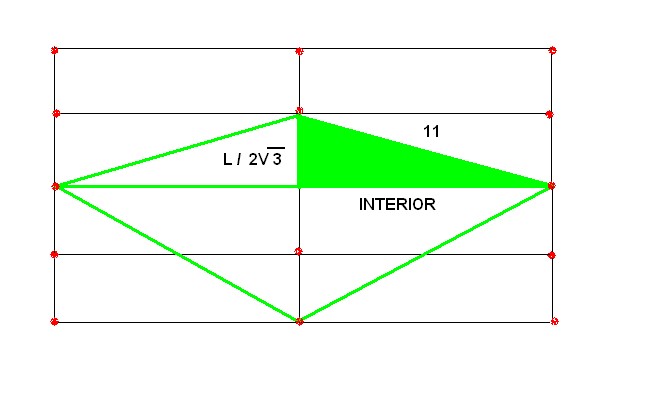
El problema es parecido al anterior. En este caso, tenemos que hallar uno de sus catetos. Queremos hallar la Diagonal mayor para un Rombo de 18 cm. De diagonal menor siendo 22 externo un valor fijo. Volveremos a la fórmula.

C² = H² - C²

                   ______________
Interior = √11 ² - (18 / 2√3) ²

                   ____________
Interior = √121 – (324 / 12)

                   ___
Interior = √ 94

Interior = 9.695

Como que el valor de la Diagonal Mayor del Rombo es el doble del hallado, debemos multiplicar por dos y obtenemos = 19.390

Para los otros valores de la diagonal menor, aplicaremos exactamente la misma fórmula.

SEGUNDO SISTEMA DE CALCULO PARA LAS MEDIDAS INTERIORES

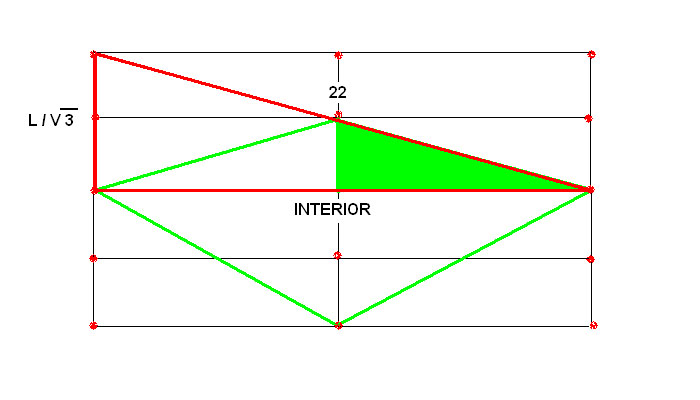
Se trata como en el otro caso de un triangulo imaginario. Volveremos a utilizar la misma fórmula.

C² = H²- C²

                   ____________
Interior = √ 22 ² - (18/ √3) ²

                   _____________
Interior = √ 484 – (324 / 3)

                     ____
Interior = √ 376

Interior = 19.390

Como vemos, es el mismo resultado que obtuvimos en el anterior cálculo.

Exponemos a continuación, la tabla de medidas interiores para 22 fijo exterior y valores de la diagonal menor.

TABLA DE MEDIDAS INTERIORES ( PARA 22 FIJO EXTERIOR)

18.00	19.390		18.50	19.233		19.00	19.070		19.50	18.901
18.01	19.387		18.51	19.230		19.01	19.066		19.51	18.897
18.02	19.384		18.52	19.226		19.02	19.063		19.52	18.894
18.03	19.381		18.53	19.223		19.03	19.060		19.53	18.890
18.04	19.378		18.54	19.220		19.04	19.056		19.54	18.887
18.05	19.375		18.55	19.217		19.05	19.053		19.55	18.883
18.06	19.372		18.56	19.213		19.06	19.050		19.56	18.880
18.07	19.369		18.57	19.210		19.07	19.046		19.57	18.876
18.08	19.365		18.58	19.207		19.08	19.043		19.58	18.873
18.09	19.362		18.59	19.204		19.09	19.040		19.59	18.870
18.10	19.359		18.60	19.201		19.10	19.036		19.60	18.866
18.11	19.356		18.61	19.197		19.11	19.033		19.61	18.863
18.12	19.353		18.62	19.194		19.12	19.030		19.62	18.859
18.13	19.350		18.63	19.191		19.13	19.026		19.63	18.856
18.14	19.347		18.64	19.188		19.14	19.023		19.64	18.852
18.15	19.344		18.65	19.184		19.15	19.019		19.65	18.849
18.16	19.340		18.66	19.181		19.16	19.016		19.66	18.845
18.17	19.337		18.67	19.178		19.17	19.013		19.67	18.842
18.18	19.334		18.68	19.175		19.18	19.009		19.68	18.838
18.19	19.331		18.69	19.171		19.19	19.006		19.69	18.835
18.20	19.328		18.70	19.168		19.20	19.003		19.70	18.831
18.21	19.325		18.71	19.165		19.21	18.999		19.71	18.828
18.22	19.322		18.72	19.162		19.22	18.996		19.72	18.824
18.23	19.318		18.73	19.158		19.23	18.993		19.73	18.821
18.24	19.315		18.74	19.155		19.24	18.989		19.74	18.817
18.25	19.312		18.75	19.152		19.25	18.986		19.75	18.814
18.26	19.309		18.76	19.149		19.26	18.982		19.76	18.810
18.27	19.306		18.77	19.145		19.27	18.979		19.77	18.807
18.28	19.303		18.78	19.142		19.28	18.976		19.78	18.803
18.29	19.300		18.79	19.139		19.29	18.972		19.79	18.800
18.30	19.296		18.80	19.136		19.30	18.969		19.80	18.796
18.31	19.293		18.81	19.132		19.31	18.965		19.81	18.793
18.32	19.290		18.82	19.129		19.32	18.962		19.82	18.789
18.33	19.287		18.83	19.126		19.33	18.959		19.83	18.786
18.34	19.284		18.84	19.122		19.34	18.955		19.84	18.782
18.35	19.281		18.85	19.119		19.35	18.952		19.85	18.779
18.36	19.277		18.86	19.116		19.36	18.948		19.86	18.775
18.37	19.274		18.87	19.113		19.37	18.945		19.87	18.772
18.38	19.271		18.88	19.109		19.38	18.942		19.88	18.768
18.39	19.268		18.89	19.106		19.39	18.938		19.89	18.765
18.40	19.265		18.90	19.103		19.40	18.935		19.90	18.761
18.41	19.261		18.91	19.099		19.41	18.931		19.91	18.758
18.42	19.258		18.92	19.096		19.42	18.928		19.92	18.754
18.43	19.255		18.93	19.093		19.43	18.925		19.93	18.750
18.44	19.252		18.94	19.089		19.44	18.921		19.94	18.747
18.45	19.249		18.95	19.086		19.45	18.918		19.95	18.743
18.46	19.246		18.96	19.083		19.46	18.914		19.96	18.740
18.47	19.242		18.97	19.079		19.47	18.911		19.97	18.736
18.48	19.239		18.98	19.076		19.48	18.907		19.98	18.733
18.49	19.236		18.99	19.073		19.49	18.904		19.99	18.729

Resumiremos el dato más relevante aportado por esta tabla:

Para 22 fijo exterior, observamos que para una diagonal menor de 18, la diagonal mayor mide 19.390 y que para una diagonal menor de 19.99, la diagonal mayor mide 18.729.

Diagonal menor 18	Diagonal menor 19.99
Diagonal mayor 19.390	Diagonal mayor 18.729

O lo que es lo mismo cuando aumenta una, disminuye la otra. En esta figura, se representa este proceso.

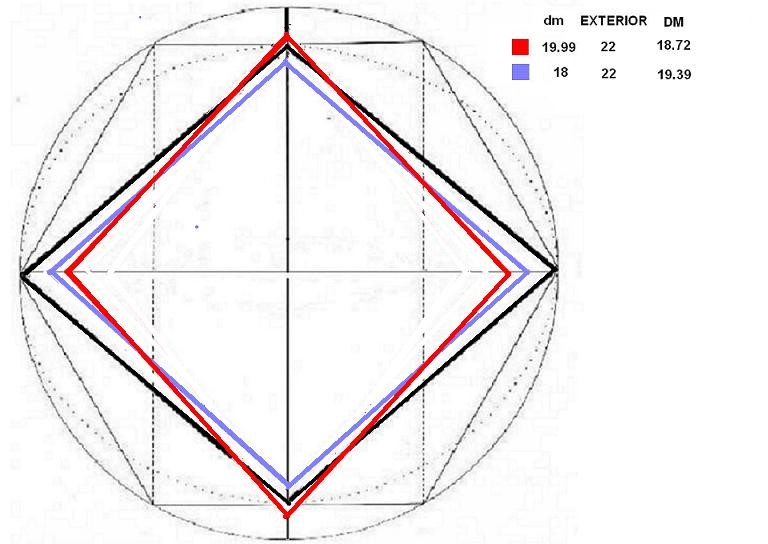
El movimiento de las diagonales

Si tenemos en cuenta que la medida exterior es fija (22), si la dimensión menor sube hacia arriba, ha de perder amplitud horizontal. Si la dimensión menor es pequeña y baja, la figura se puede hacer más amplia. Si el Rombo es alto, es estrecho y si el Rombo es bajo, es ancho.

En teoría, el estudio geométrico de las figuras tridimensionales 22 interior 22 exterior acaba aquí. Pero la geometría parece ser la plasmación tridimensional de ideas y conceptos abstractos, así que es fácil dejarse llevar por la imaginación y buscar esos conceptos una vez que se han encontrado unos números. Por esto, pienso que se pueden llegar a algunas consideraciones que seguramente no son más que el punto de partida de algún estudio posterior.

CONSIDERACIONES

1. Presencia de un punto critico.

En la siguiente tabla, que es un trozo de la anterior, situamos a la izquierda el tamaño de la diagonal menor y a la derecha, vemos el de la diagonal mayor. Como observamos, a medida que la diagonal menor se va haciendo más grande, el tamaño de la diagonal mayor se hace progresivamente más pequeño, pero siempre es mayor que el tamaño de la dimensión menor. Veremos que, en un momento dado, los valores de la derecha superan a los de la izquierda. Pero hay un instante crítico, un tamaño preciso de la diagonal menor que es exactamente igual a la diagonal mayor. Es solo un instante de equilibrio. La tabla de la izquierda y de la derecha, se igualan. Se trata de una diagonal menor muy conocida. De hecho, ha sido la cifra de la diagonal menor más estudiada y sobre la cual se han hecho más dibujos. Es la única diagonal menor que permite inscribir al Rombo dentro de un hexágono regular. Ella fue el motivo de todos los dibujos que se hicieron en el estudio sobre 18-19. Es un valor que más o menos recordamos.: 19.05255888

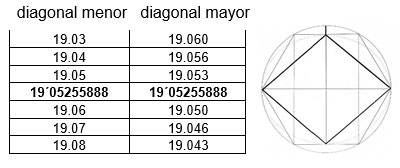
A partir de ese instante, como vemos, la diagonal menor supera a la mayor. Hay un antes y un después a partir de 19.05. Le seguimos llamando diagonal menor, pero, de hecho, se ha transformado en la mayor. No debe ser casual que ese Rombo sea el único que permite su dibujo en el hexágono. Es un Rombo particular y situado aproximadamente a medio camino entre el 18 y el 19.999

Ese instante crítico, ese momento, permite que la diagonal menor se transforme en mayor y viceversa. Se produce un cambio estructural muy importante, ya que hay un cambio de polaridad.

Estas inversiones, se dan continuamente, pero no tiene más importancia que la marcar el fin de algunas secuencias de la vida y de la naturaleza. Estos cambios de polaridad, pueden marcar el principio y el final de muchos procesos, y aunque desconocemos su mecanismo de acción, es lógico pensar que su importancia está relacionada con el lugar donde se produce este cambio. Esto ofrece la posibilidad teórica, si se conoce este proceso, de poder evitar ciertos cambios vitales que pueden ser no deseados.

2. Aparición del cuadrado crítico.

Bien, ese punto crítico lo podemos dibujar en la figura. Hemos de recordar que el dibujo que tenemos abajo es el de 22 interior. Sobre él, proyectamos este dato del punto crítico, basado sobre el 22 exterior

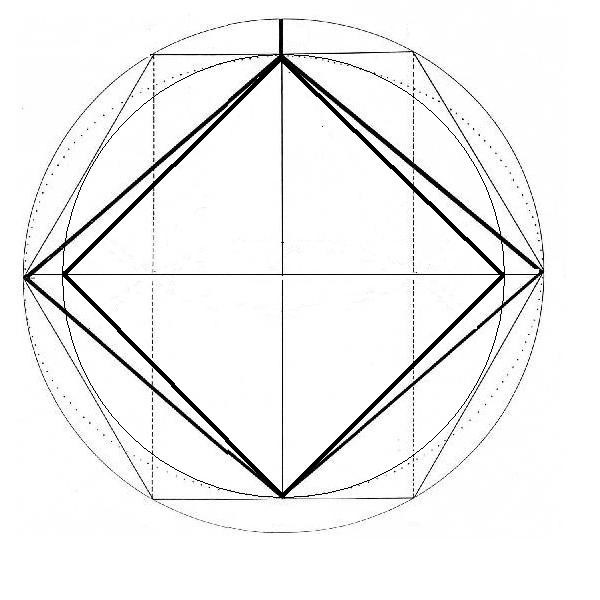
Ha aparecido el cuadrado dentro del Rombo

Aquí tenemos al cuadrado. Representa un momento crítico, una zona de equilibrio, de frontera y de transición. En la siguiente figura, el punto crítico lo señalamos en verde. Ahora plasmaremos los otros valores, para la diagonal menor 18, marcamos su valor, que es de 19.390 (violeta) y para la diagonal menor 19.99, representamos su valor que es 18.729 (rojo)

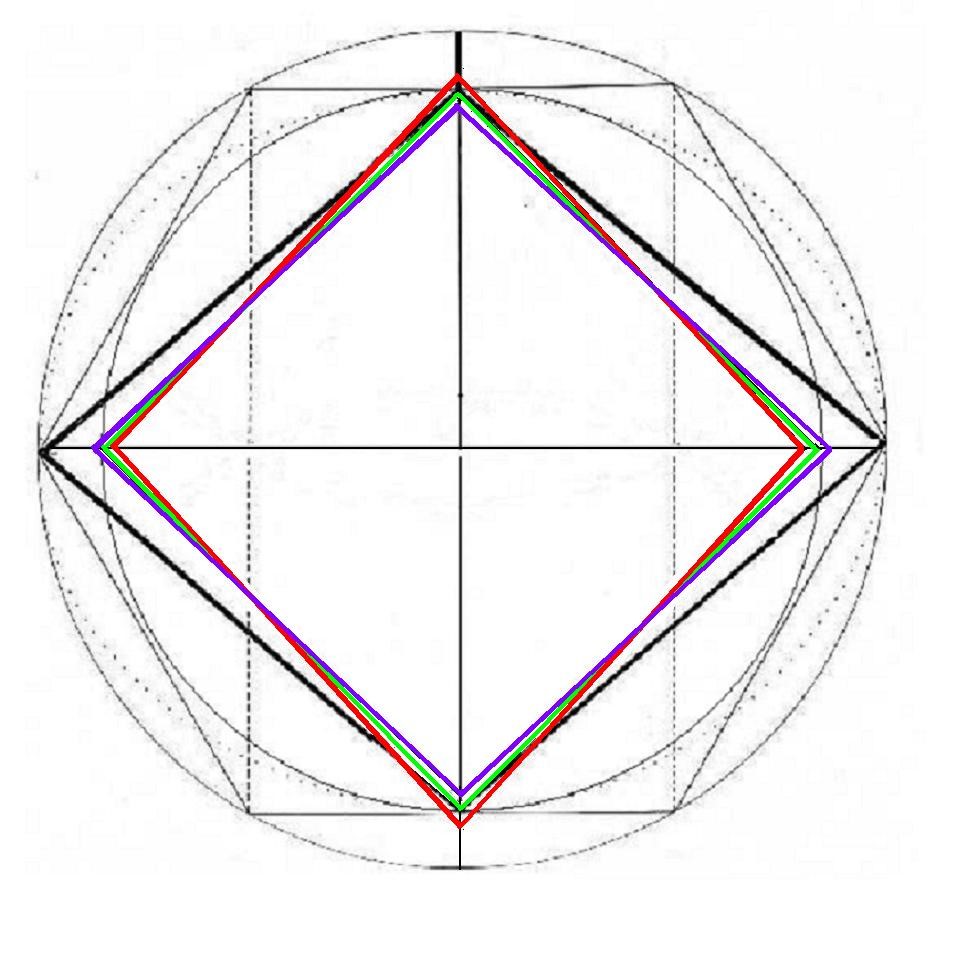
Antes y después del cuadrado crítico

El Rombo tridimensional 22 exterior respira y este movimiento fisiológico, se puede seguir en el eje de la diagonal menor y en el eje de la diagonal mayor

3. La media de las diagonales mayores para 22 exterior coincide con el punto crítico.

Este es otro dato curioso. Si de esta tabla de 22 exterior, hacemos la media aritmética de los 200 valores hallados tendremos la cifra media de la diagonal mayor para todos los valores comprendidos entre 18 y 19.99

19.90	18.761
19.91	18.758
19.92	18.754
19.93	18.750
19.94	18.747
19.95	18.743
19.96	18.740
19.97	18.736
19.98	18.733
19.99	18.729
200	3.813.468

El resultado es 3.813´468 / 200 = 19.06, un valor muy aproximado a 19.058…

Con ello quiero decir que la cifra encontrada en su día de diagonal menor única permitida en el hexágono regular está sorprendentemente cerca de la cifra media aritmética de la diagonal mayor para todos los Rombos posibles entre 18 y 19.99 para 22 exterior.

No quisiera caer en un error o en una alucinación, pero el valor hallado en su día era para la diagonal menor, y no para la media de la diagonal mayor del Rombo 22 exterior. Lo que sucede es que ambas cifras, se parecen demasiado, teniendo en cuenta sobre todo que solo he trabajado con 3 decimales y que la aproximación podría ser mayor, quizá casi total.

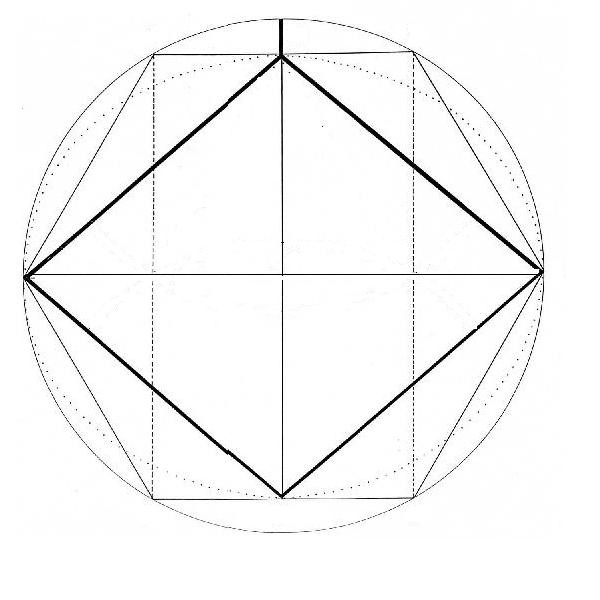
La media de las diagonales mayores para 22 exterior es aprox. 19.058

4. El aire de una pirueta antigua

Sin querer, se llega a conclusiones, que son de lo más obvias, pero que extrañan. Por ejemplo, 19.05 es la cifra de la única diagonal menor que se puede inscribir en el hexágono regular y que está calculada para un rombo de 22 interior, pero que al mismo tiempo es la media o de todas las diagonales mayores posibles para el Rombo de 22 exterior. Sería como decir que la diagonal menor y la mayor son una misma cosa. Aquí se debería hacer una gran pirueta para entender todo esto.

Me acuerdo de que ya hace un tiempo, apareció otra gran pirueta de las diagonales, cuando vimos que en un Rombo en giro e inscrito dentro de otro, la diagonal menor de un Rombo se transformaba en la diagonal mayor de otro.

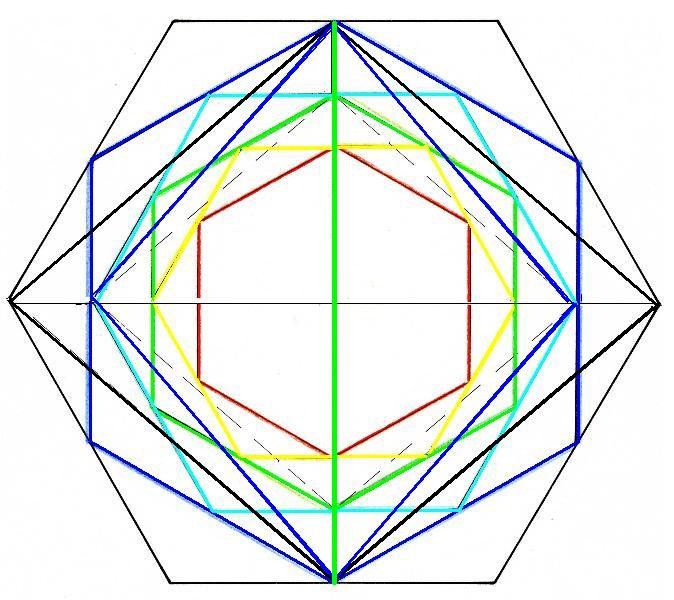
La diagonal menor del negro ha pasado a ser la mayor del azul

En el hexágono negro, tenemos el Rombo negro y dibujada en verde la diagonal menor. En el hexágono azul interior, tenemos al Rombo azul y aquí, la misma diagonal menor, ahora es la mayor. La diagonal menor y mayor se van alternando. Son la misma cosa, pero en un Rombo aparece como la diagonal menor y en el otro Rombo es la diagonal mayor.

Cuando apareció este dibujo, comprendí que existía un juego de alternancia con la 4ª D, y que quizá estábamos frente a una pirueta de significado oculto.

Podría ser que la cuarta dimensión estuviera vinculada con giros, movimientos, alternancias y otros fenómenos “ópticos”. Fue un momento en el que la 4ª D

(O lo que es lo mismo, la diagonal menor y la mayor) empezaron a permutarse y parecían decir: “Cuando me buscas a mí, encuentras a la otra”.

Ya nada parecía sólido y rígido. Parecía que todo fuera cambiante, formando parte de un juego parecido al escondite. Cuando creo que te tengo, te vas.

Ahora, vuelve a aparecer otra pirueta, quizá relacionada con ésta, pero vista desde otro ángulo, dibujada de otra manera, y tan curiosa como la otra.

Buscas la diagonal mayor de 22 exterior, y de repente parece que te encuentras con una diagonal menor. Esto parece un juego en el que intervienen dos Rombos jugando a mezclarse e inter penetrarse.

5. El porque de un STOP

 

El Rombo se ha de mover entre 18 y 19.999999, pero no puede llegar al 20. Ha de existir alguna regla matemática, alguna cifra que impida que se llegue hasta allí.

Volveremos a recordar el dibujo que nos permitió realizar el cálculo exterior.

La fórmula que hallamos para el cálculo era la siguiente:

                                            ______________
                                    E = √ (L / √3)² + 22 ²

Y en base a esto, elaboramos la gráfica de resultados de las medidas exteriores que enseñamos antes.

Ahora, quisiera ampliar esa gráfica un poco más y detenerme en algunos aspectos del cálculo. Esta gráfica que exponemos a continuación no es la completa (faltan valores) y he introducido asteriscos para señalar algunas curiosidades numéricas.

Para empezar, quisiera decir que la tabla tiene algunos detalles muy curiosos. Por ejemplo, el primer valor, el de 18, da como resultado un número natural, sin decimales. Todas las demás cifras tienen decimales. La segunda curiosidad se da al final de la tabla. A partir de 19.90, empiezan a aparecer cifras que en el cuarto o quinto decimales se vuelven periódicas y al final de la tabla, he querido desarrollar con más detalle la aproximación hacia el 20. Como vemos, a medida que van apareciendo nueves, nos vamos acercando a una fracción periódica pura, que aparece en el número 20.

	TABLA DE VALORES PARA 22 INTERIOR
L	h ² = ( L / √ 3) ²		E = √ h²+484
LADO TRIANGULO			EXTERIOR
18.00	108	*	24.331
18.01	108.120		24.333
18.98	120.080		24.578
18.99	120.206		24.580
19.00	120´3333333333333	**	24.583
19.01	120.460		24.585
19.02	120.586		24.588
19.88	131.738		24.814
19.89	131.870		24.816
19.90	132.003	*	24.819
19.91	132.136	*	24.822
19.92	132.268		24.824
19.93	132.401	*	24.827
19.94	132.534	*	24.830
19.95	132.667		24.832
19.96	132.800	*	24.835
19.97	132.933	*	24.838
19.98	133.066		24.840
19.99	133.200	*	24.843
19´999	133.320		24.845
19´9999	133.332		24.846
19´99999	133´3332		24.846
19´999999	133´33332		24.846
19 ´9999999	133´333332		24.846
19´99999999	133´3333332		24.846
20.00	133´3333333333333	**	24.846

En la cifra 20.00 se produce una fracción periódica pura. Es una vibración sostenida, sin cambio. Una sola nota que se repite una y otra vez hasta el infinito, causando una vibración peligrosa, sin oscilaciones, capaz de romper estructuras.

Puede que esta sea la causa matemática y vibracional por la que el Rombo no puede llegar a este punto crítico.

La misma situación, o parecida se da justo en la mitad matemática de la tabla, en el punto 19, hallazgo que da que pensar, naturalmente.

Curiosos datos, extraídos de una tabla, en la que vemos que el Rombo, parece ir del número natural a la fracción periódica pura.

Siempre nos sorprende cualquier hallazgo, por pequeño que sea, y es que como dice Rosa, el Rombo nos va dando perlas.

6. La intersección de Rombos a 90º

Cuando dibujé por primera vez el Rombo inscrito dentro del hexágono, apareció una figura ya muy conocida y luego, asomó la segunda otra.

Las dos figuras que aparecieron

La primera representaba al Rombo en proyección frontal, y la otra era una proyección lateral. Lo curioso es que ambas figuras, estaban inscritas dentro del hexágono regular. No lo esperaba. Ni lo primero, ni lo segundo. Se podía hacer coincidir las dos figuras. Nos hacía falta una figura más compleja que el hexágono. Aquí, debíamos recurrir al dodecágono. Aquí se veía perfectamente como el Rombo frontal y el lateral se ensamblaban uno dentro del otro.

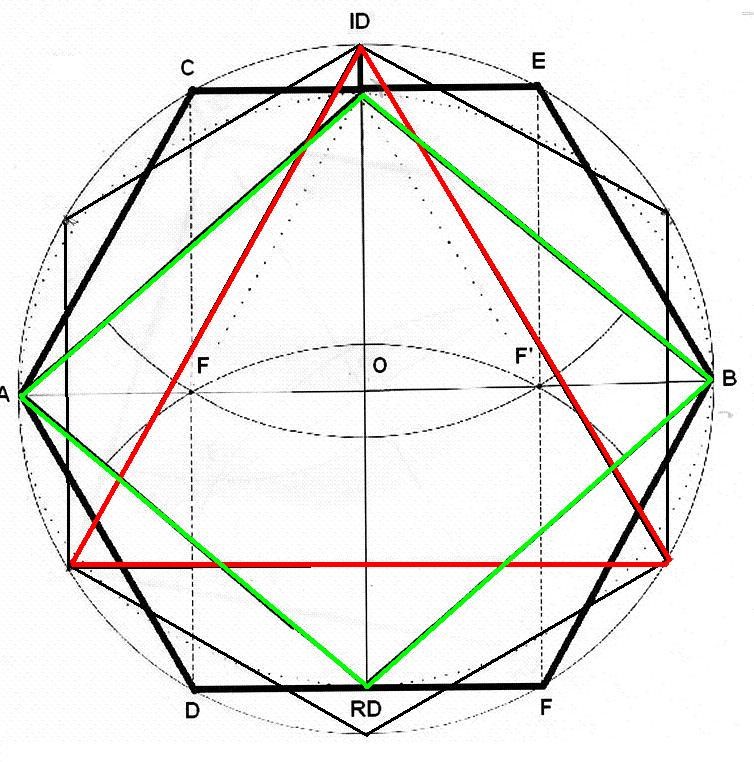
Una figura compleja

Esta imagen, curiosísima tiene muchas lecturas. La primera es que tenemos delante un Rombo verde, horizontal, que es atravesado por otro rombo que va de delante hacia atrás. Son dos Rombos fusionados, ensamblados perfectamente por la 4ª Dimensión, aportando un punto de simetría y de equilibrio, siempre necesario para el funcionamiento correcto del Rombo. De otra manera, se produciría un desequilibrio de todo el sistema.

Interacción

El punto central del chip (En rojo) se corresponde con la diagonal mayor, y se desplaza por el eje de la 4ª D. El chip de todas las leyes del universo se puede desplazar a cualquier dimensión Este gráfico representa como interaccionan la materia y la conciencia. Quizá por eso si la conciencia esta centrada en la 4º D, se puede interactuar de una manera eficaz sobre la materia, produciendo interacciones completas. Si el chip se encuentra en la 6ª D, y si la persona está viviendo en ese nivel, la interacción, puede dar, por ejemplo, la posibilidad de manipular las estructuras atómicas

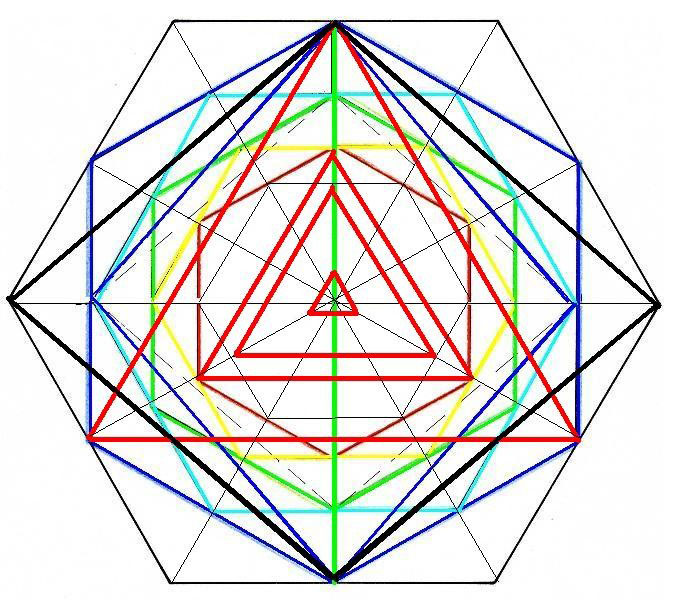
Interacción de chip y planos

El Rombo de planos de conciencia es atravesado por un chip universal. La interacción entre materia y conciencia será muy diferente según sea el lugar de la transacción.

Para cerrar esta consideración, que abre muchísimas posibilidades de estudio, me gustaría recordar que uno de los motivos que me sugirió la idea de los Rombos cruzados en perpendicular fue la forma que tienen las radiaciones electromagnéticas. Si la electricidad se mueve en un plano, el magnetismo, lo hace en otro plano perpendicular al anterior.

La idea, venía a sugerir que podría ser que un Rombo estuviera relacionado con cuestiones más físicas (chip universal) y el otro, tuviera una expresión más magnética (planos de conciencia).

7. Los cuatro arquetipos del Rombo

Repasemos y veremos que actualmente, hemos pasado de un solo arquetipo del Rombo a cuatro.

Rombo bidimensional 22 interior.

Es el primer Rombo que conocimos. Tiene la síntesis de todas las leyes del Rombo. Está relacionado con el ser humano.

                                     

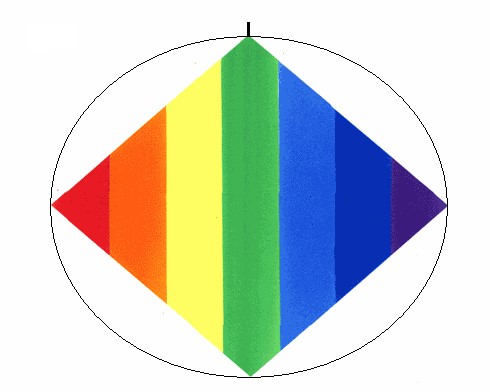
Figura bidimensional 22 interior

Rombo bidimensional 22 exterior

Es el Rombo que surge como resultado de la proyección del Rombo            tridimensional 22 exterior. Es la proyección en plano del chip universal.

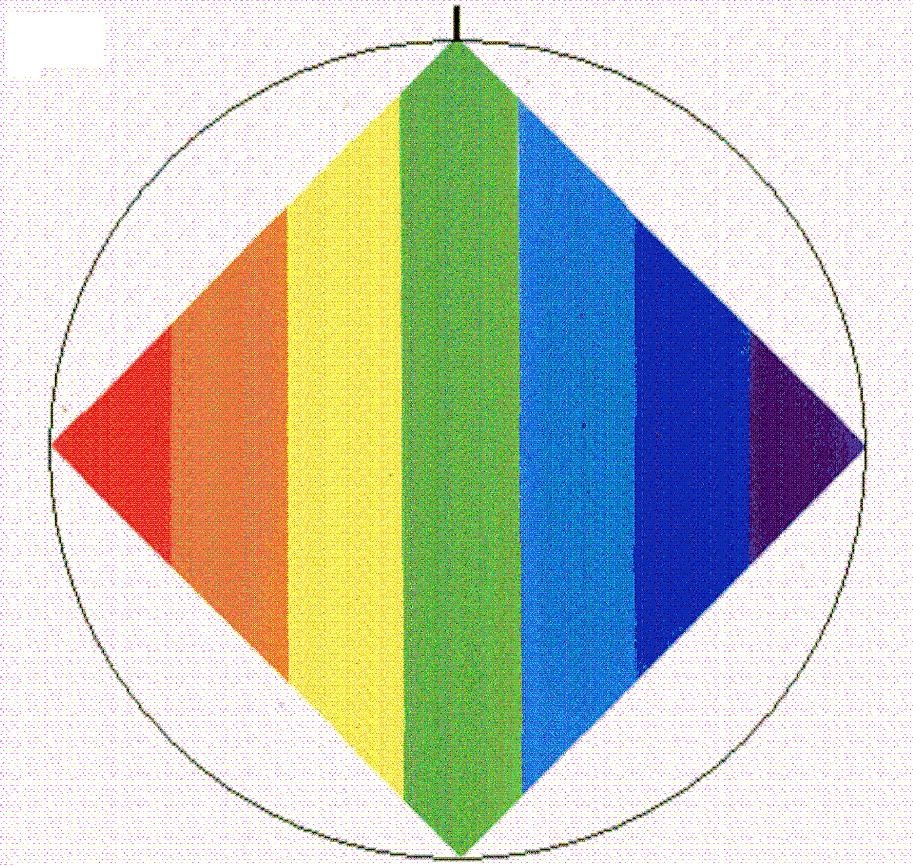
Figura bidimensional 22 exterior

Es un Rombo más variable que el anterior. Por un lado, tiene al igual que la otra figura plana, la movilidad de la diagonal menor (18-19.9) y además disfruta de la movilidad de la diagonal mayor (18.72 – 19.39).

Rombo tridimensional 22 interior

Es el Rombo interior del hombre. Con el sabremos encontrar y discernir los estados físicos y mentales del ser humano y que lo hacen crecer hasta convertirse en un criatura evolucionante cósmica.

Tridimensional 22 interior

Rombo tridimensional 22 exterior

Este Rombo, nos dará el conocimiento de las leyes universales exteriores al ser humano y de la belleza de estas estructuras. Es el chip universal de las leyes del universo.

Toda la creación, lleva incorporada dentro de sí las mismas leyes universales que están en el Rombo. Es el sello, la marca del creador, su firma. Todo se ha hecho de la misma manera, nada queda fuera y todo sigue el mismo patrón. El Rombo enseña cuáles son esas líneas maestras adaptables y leíbles en cualquier laboratorio en que se estudien.

Tridimensional 22 exterior

8. Las posibilidades

De momento, lo dejamos aquí. Parece evidente, que el tema es muy amplio y seguro que tendrá que ser estudiado y meditado. Hay cuestiones que asoman la cabeza, como la asimetría bascular que no dejan indiferente y que siempre aportan nuevos caminos, porque la asimetría siempre está presente y llena de contenidos en el Rombo.

22 fijo interior       24.843 – 24.331 = 0.512 22 fijo exterior     19.390 – 18.729 = 0. 661

Otros temas, comentados superficialmente, como la inversión del Rombo y la interacción entre el chip universal y los planos de conciencia, ofrecen un campo maravilloso de estudio. Todo ello, me parece un espacio vacío con necesidad de ser llenado. Pero bueno, seguramente, por hoy, tenemos bastante. La idea del artículo era iniciarnos en el Rombo tridimensional y empezar a darle cifras, contenidos y posibilidades. Creo que el primer paso está hecho. Ya daremos el segundo.