La figura bidimensional del Rombo

RAZONES GEOMÉTRICAS

Este escrito está orientado al estudio matemático y geométrico de este dibujo tan sencillo del Rombo bidimensional. Este dibujo, fue el que apareció primero y que generó toda la serie de diseños más complejos y mucho más elaborados que aparecieron con posterioridad.

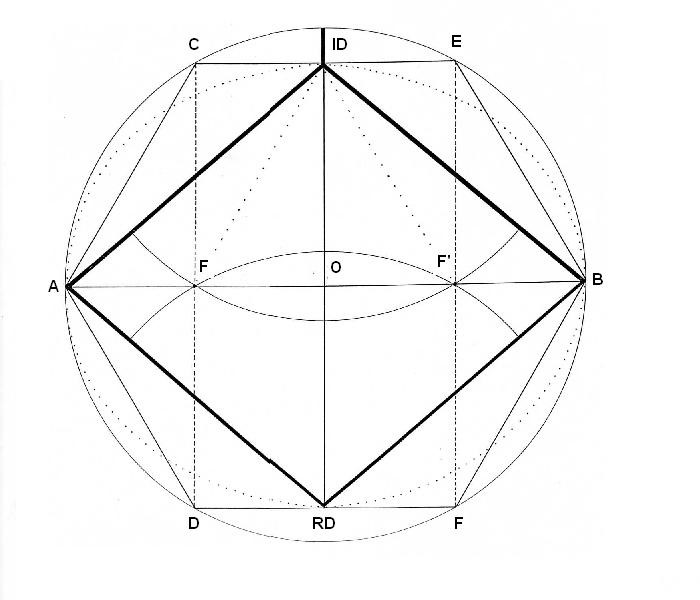
Figura. El primer dibujo de la serie

Para este estudio, tendremos la ayuda inestimable del teorema de Pitágoras, que nos ayudará a calcular los diferentes valores del Rombo a partir del hexágono regular. Veremos que son solamente 8 dibujos y cada uno de ellos tiene una explicación de las operaciones que se realizan.

1. DETERMINACION DE LA MEDIA DIAGONAL MENOR DEL ROMBO

Partimos de un hexágono. El punto central es el punto O. La circunferencia que ha permitido dibujar el hexágono tiene radio R, que es equivalente a cualquiera de sus lados. Ahora, estudiaremos el triángulo BOA. Intentaremos determinar la apotema OI. Esta apotema será la clave para entender todos los posteriores dibujos.

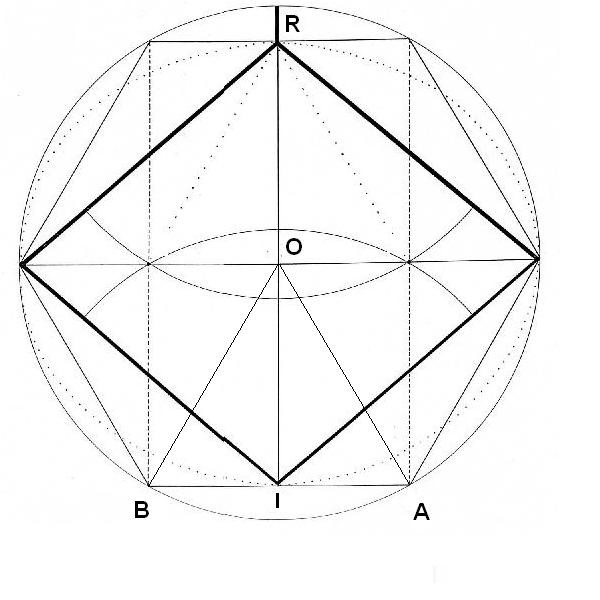
Figura. Determinación de media diagonal menor

Para buscar la apotema, aplicamos Pitágoras, y obtenemos:

___________

OI = √(AO)²-(AI)²

_________

OI =√R²-(R/2) ²

_________

OI =√ R²-R²/4

______

OI =√3R²/4

OI = R √3

_____

Que es la fórmula que relaciona el radio y la apotema del hexágono (que en nuestro caso es la mitad de la diagonal menor del Rombo). Para un Rombo construido con un radio de 11cm, la mitad de la diagonal menor valdría:

11 x √3

Media diagonal menor = ____________ = 9.526279442

2. LA DIAGONAL MENOR DEL ROMBO PARTIENDO DE LA APOTEMA

Si observamos el dibujo, veremos que la diagonal menor es por construcción el doble que OI, (la apotema hallada) así que deducimos:

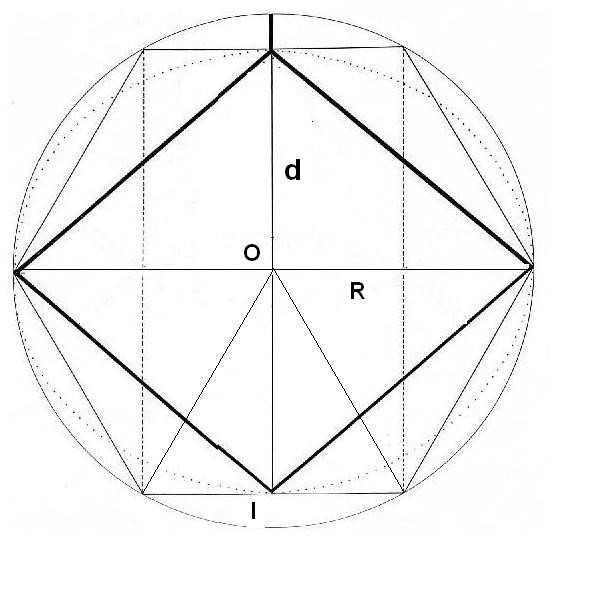
Figura. La diagonal menor del Rombo partiendo de la apotema

d = 2 OI

___

d = 2 R √3

_____

___

d = R √3

Que es la fórmula que nos relaciona el Radio de la circunferencia exterior y la diagonal menor del Rombo. En un Rombo hecho con un radio de 11 cm, la diagonal menor valdría

___

d = 11 √3 = 19.05255888

3. VALOR DE UN LADO DEL ROMBO

Disponemos de un triángulo en el que conocemos dos lados y queremos determinar el tercero. Conocemos un cateto, conocido como R, y el otro ,nombrado como d cuyo valor es

R √3

_____

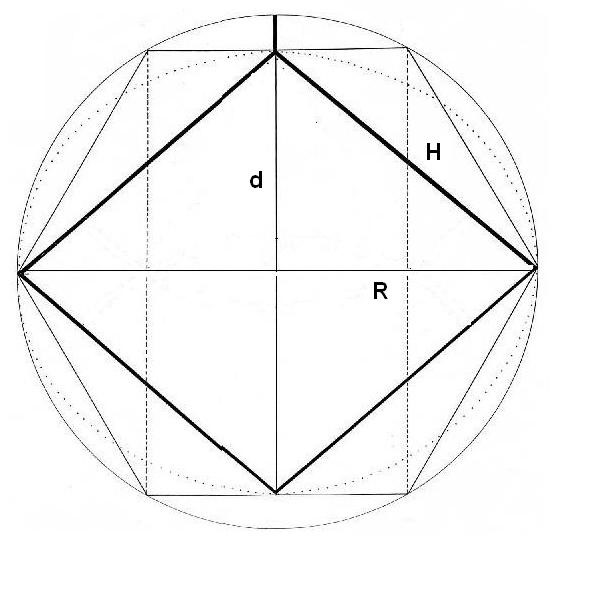
Figura. Valor de un lado del Rombo

Queremos hallar el valor h, que es la hipotenusa del triángulo y que corresponde al valor de todos los lados del Rombo. Por Pitágoras, tenemos que

______________

h = √R²+ )R √3 (²

____________________

2 ²

___________________

h = √ R² +) R √3(²

_______

_____________

h = √ 4 R² + 3R²

___________

_____

h = √ 7 R²

______

___

h = R √7

____

Con lo que obtenemos el valor que íbamos buscando. El valor de cada lado del Rombo está relacionado con el radio de la circunferencia de esta manera.

En nuestro Rombo, cada lado tiene este valor:

___

√7

Lado = 11 ____ = 14.55163221

4. HALLANDO LA DIAGONAL MAYOR DEL ROMBO

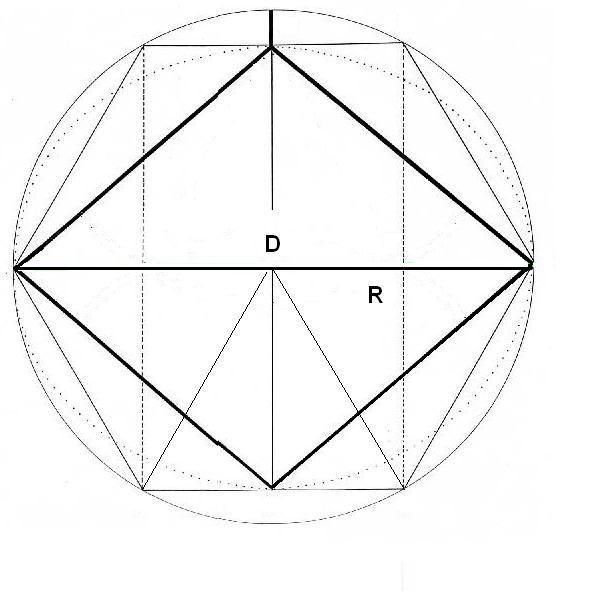
Figura. La Diagonal mayor del Rombo

Se trata de determinar la Diagonal Mayor del Rombo. Conocemos un lado del Rombo, que es la hipotenusa y un cateto, que es media diagonal menor. Intentaremos hallar el otro cateto, que es la mitad de la diagonal mayor

Sabemos que un cateto que en este caso es media diagonal menor mide:

____

R √ 3

‾‾‾

Y que la hipotenusa, que es un lado del Rombo vale:

____

R √ 7

‾‾‾

Por lo tanto, aplicaremos Pitágoras para hallar el cateto que nos falta.

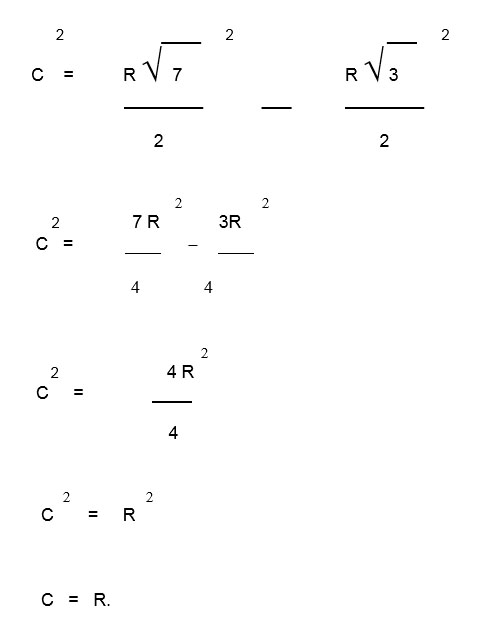
Es decir, el cateto es igual al radio. Como que la Diagonal mayor es igual a dos radios tenemos que

D = 2 R.

En nuestro Rombo, la Diagonal Mayor es igual a 2 x 11 = 22 cm.

5. RELACION ENTRE LAS DIAGONALES DEL ROMBO

Buscaremos una relación entre ambas diagonales. Partimos de dos datos ya conocidos. Por un lado, la Diagonal Mayor, que es igual a 2R y la diagonal menor, cuyo valor R√3

determinado fue determinado antes.

Diagonal Mayor = 2 R__

Diagonal menor = R√3

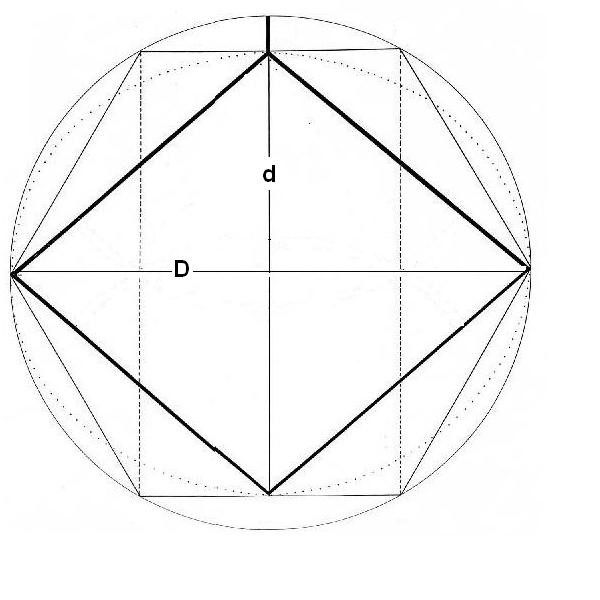
Figura. La razón entre las diagonales

Estudiamos la segunda ecuación:

Segunda ecuación

Con lo que obtenemos la Diagonal mayor a partir de la menor. Podemos ahora, realizar lo inverso e ir a determinar la diagonal menor a partir de la mayor. Partimos otra vez de las primeras igualdades.

Segunda ecuación

Con lo que obtenemos la diagonal menor a partir de la mayor. Vamos a realizar el cálculo práctico de los valores que hemos hallado. Veremos si coinciden los valores de la fórmula con las cifras conocidas: La Diagonal mayor se obtiene multiplicando la diagonal menor por el factor de expansión

Segunda ecuación

6. RELACION ENTRE DIAGONALES Y FOCOS DEL ROMBO

Intentaremos hallar la relación entre las diagonales y los focos

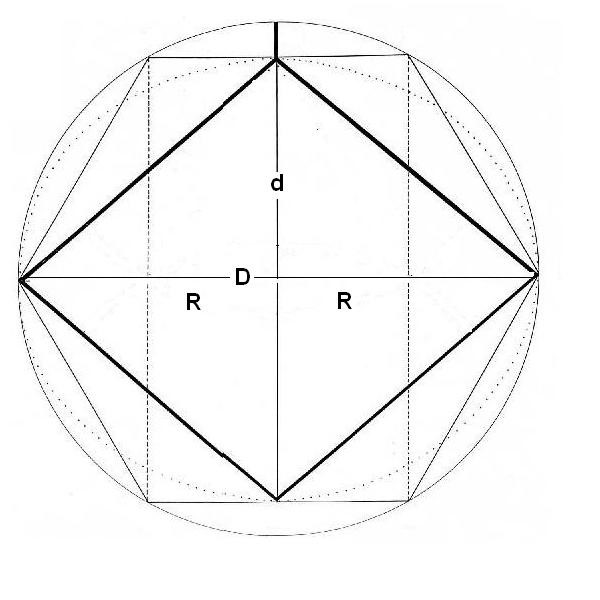
Figura. Relación entre diagonales y focos

La diagonal mayor es igual a dos radios

D = 2R

Como que el radio es igual 2 focos

D = 4F

Sabemos por haberlo hallado que la diagonal menor es igual a

d = R √ 3

y sustituyendo R por 2F, tenemos que

d = 2F √ 3

de donde obtenemos las dos fórmulas que relacionan diagonales y focos

D = 4F

___

d = 2F √ 3

En nuestro Rombo D = 4 x 5.5 = 22

d = 2 x 5.5 x √ 3 = 19.05255888

7. CALCULO DE LA DISTANCIA FOCO - ID

Determinaremos la distancia entre Foco e ID. Sabemos que la circunferencia exterior al hexágono está hecha con Radio R, que es igual al doble de OF. Entonces, OF = R/2. También conocemos a OID, cuyo valor hemos hallado al determinar la apotema y que era…

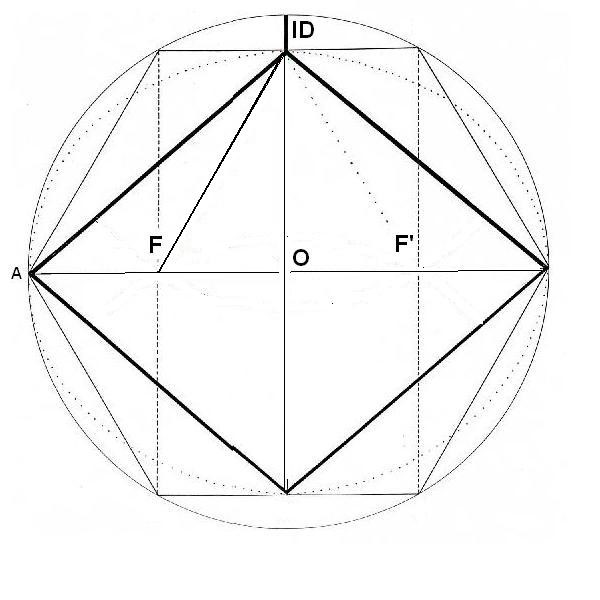
Figura. Distancia Foco - ID

√ 3

OID = R _____

Por Pitágoras sabemos

______________

FID = √ (OF)² + (OID)²

___________________

FID = √ (R/2) ² + (R √ 3 / 2)²

___________________

FID = √ (R²/4) + (3R² /4)

_________

FID = √ 4 R²/4

___

FID = √ R²

FID = R

Con lo que tenemos que la distancia desde el Foco a ID es igual al Radio. En el Rombo la distancia entre el Foco e ID es igual al Radio = 11

8. VALOR DEL FOCO DEL ROMBO

Partimos del triángulo ADO. Sabemos que la apotema AF, tiene el mismo valor que la mitad de la diagonal menor del Rombo. Según determinamos antes, el valor de AF era:

___

R√3

AF = _____

Queremos estudiar el foco FO. Por Pitágoras, sabemos que:

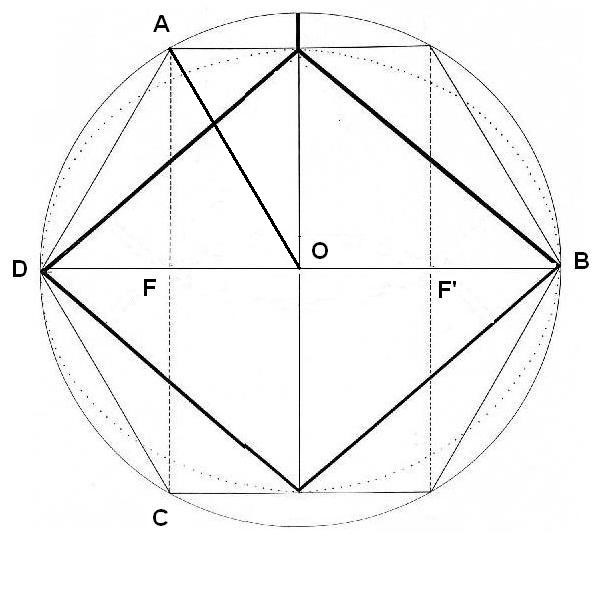
Figura. Valor del foco del Rombo

______________

FO =√ (AO)² - (AF)²

_______________

FO =√ R² -(R√3/ 2)²

_______________

FO = √ 4R²-3R² / 4

_________

FO = √ R²/ 4

FO = R / 2

Vemos que el Foco es la mitad del radio de la circunferencia. Entonces, tendremos que la distancia entre focos (F-F’) será igual a R.

F – F’ = R

En el Rombo, la distancia entre el foco y el centro es

FO = 11/ 2 = 5.5 cm.

Y la distancia entre focos:

F-F’ = 11 cm.

Y con estas razones matemáticas que acabamos de ver, finalizamos este pequeño estudio que tenía como motivo empezar a encontrar proporciones escondidas en la arquitectura interna del Rombo.

Nos gustó encontrar las proporciones que existían entre los diferentes componentes de la construcción del Rombo, y a ver la importancia que empezaba a cobrar la situación de los focos para la realización de las elipses. Empezamos a darle importancia al hexágono exterior y a familiarizarnos con él ya que aparecería posteriormente en muchos otros trabajos y en los que vimos que actuaba como un soporte estructural exterior a toda la arquitectura del Rombo. Toda esta matemática elemental nos sirvió para empezar a descubrir las maravillas geométricas que más tarde empezamos a desvelar. Esta geometría elemental, dio paso a la geometría sagrada.

LA GEOMETRIA SAGRADA EN EL ROMBO

Hacía mucho tiempo que debatíamos dentro del grupo acerca de la medida exacta de la diagonal menor del Rombo. Sabíamos que era un valor muy poco indefinido (18-19) así que pensamos que la única manera de resolver el enigma era acudir a la geometría. El primer paso que hicimos en el estudio de la figura fue situarla dentro del hexágono y el círculo. Dibujamos una circunferencia de 11cm. de radio. Con el mismo radio, dibujamos el hexágono. Unimos algunos puntos del hexágono y obtuvimos un Rombo. Desde ID y RD y con el mismo radio, obtenemos dos puntos de cruce en la diagonal mayor. Son los puntos F y F. (Focos de la elipse). Unimos los vértices C-D y E-F y también obtuvimos los focos. Trazamos la elipse a partir de estos dos puntos con el método del jardinero. Constatamos la aparición del triángulo (F-ID – F’). Observamos la línea de la ID. En este dibujo, tiene una longitud determinada, que es la distancia que va desde el Rombo a hexágono exterior.

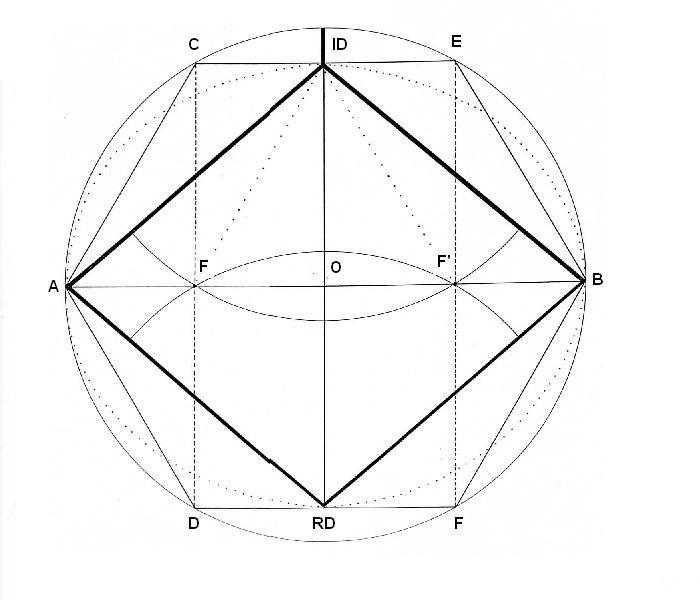
Figura. El Rombo dentro del hexágono

Con el radio, desde F y F, hacemos llegar curvas a la circunferencia exterior. Se crean los puntos A, A, B y B’. Desde estos nuevos puntos y con el mismo radio, se crean semicírculos que unen focos y centro. También se crean diversos puntos en la circunferencia exterior. Desde los focos se dibuja la elipse. Un punto cualquiera de ella (E), está unido por un brazo corto y uno largo a los focos. Su suma es constante e igual a 22 cm.

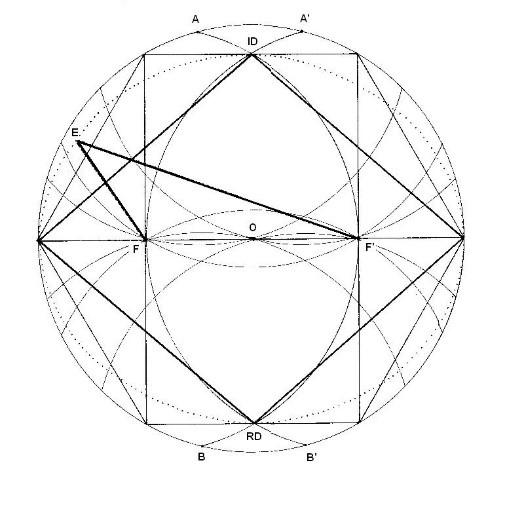
Figura. Características de los focos

Conocemos un cateto, que es el foco. También tenemos el valor de la hipotenusa (que es el valor del radio de la circunferencia). Sólo nos falta el valor del otro cateto. Lo determinamos por la fórmula del teorema de Pitágoras. Al final de la operación, su valor es 19,05255588…con este dato concreto, ya se podría haber acabado el estudio de los dibujos porque era el dato buscado, pero seguimos adelante estudiando más aspectos de la geometría.

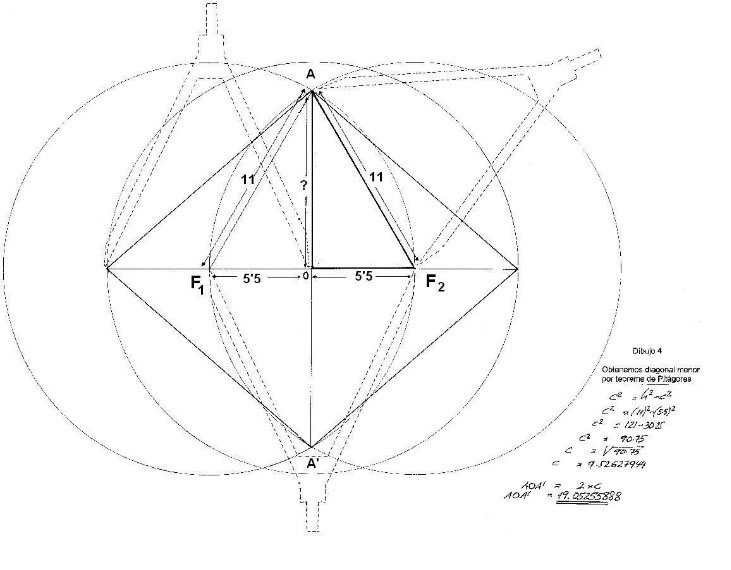
Figura. Diagonal menor en el Rombo inscrito en hexágono

Desde los vértices del hexágono, trazamos círculos que se unen en el centro formando una margarita. Vemos también como pueden aparecer en los extremos nuevas margaritas

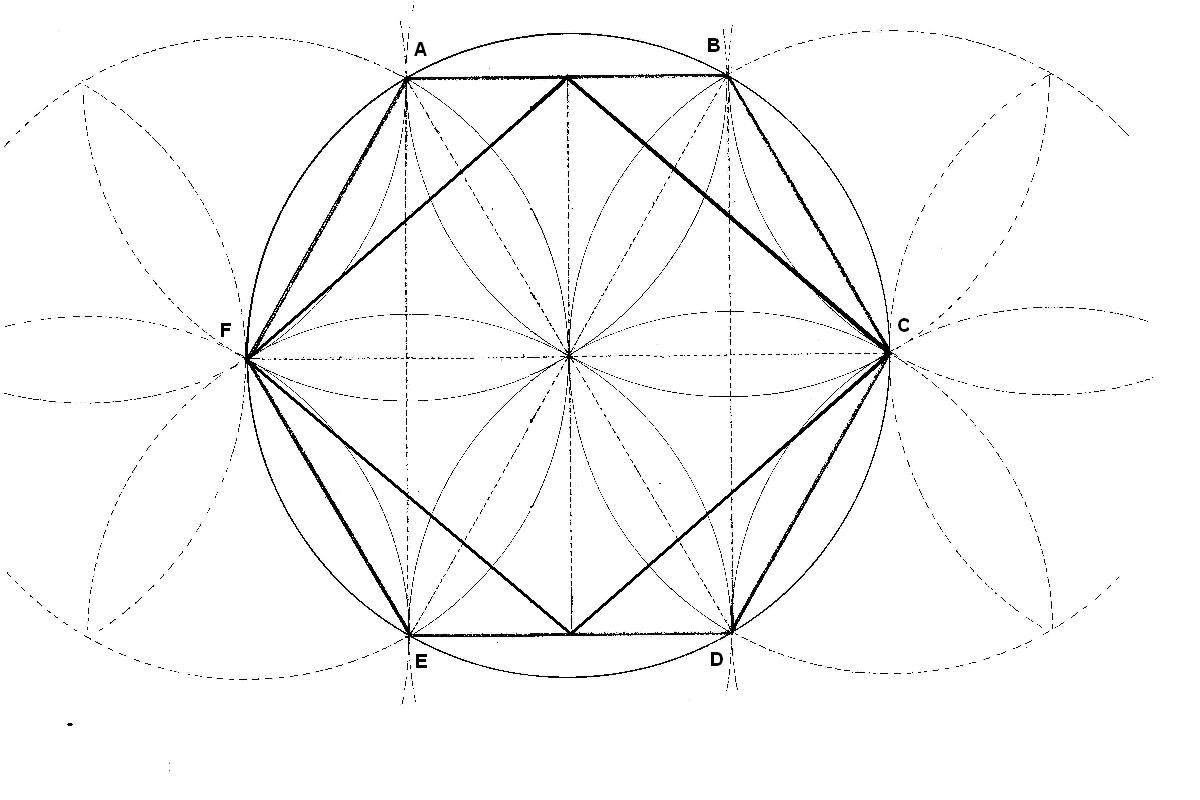
Figura. El centro radial y las margaritas

Dibujamos 2 hexágonos, uno dentro del otro. Ahora los centros de las margaritas están en los focos. El centro radial del hexágono se convierte en un foco. El foco tiene propiedades geométricas iguales a las del centro. El foco es un centro de equilibrio de la figura. De hecho, cuando estudiamos la cruz del Rombo, ya vimos que éste, se sustenta en tres puntos principales. Son el centro y los dos focos.

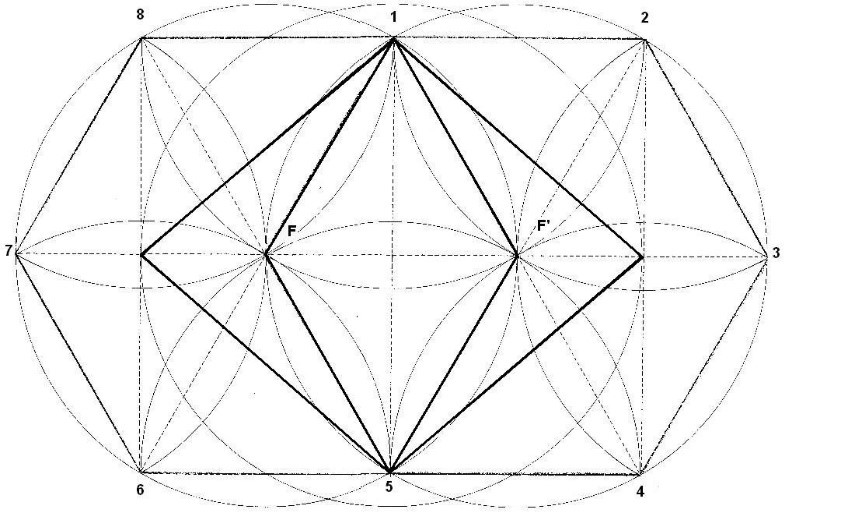
Figura. Los focos son también el centro

Se trata de una composición de dos los dibujos anteriores. Las margaritas están en el centro y los focos. Los dos focos parecen ser la separación del centro hacia un lado y otro de la creación. Si el centro, se desplazara a ambos lados, se crearían los focos. Si los focos se desplazaran hacia el centro, aparecería el centro O. Es inevitable querer ver una movilidad desde el centro a los focos y viceversa.

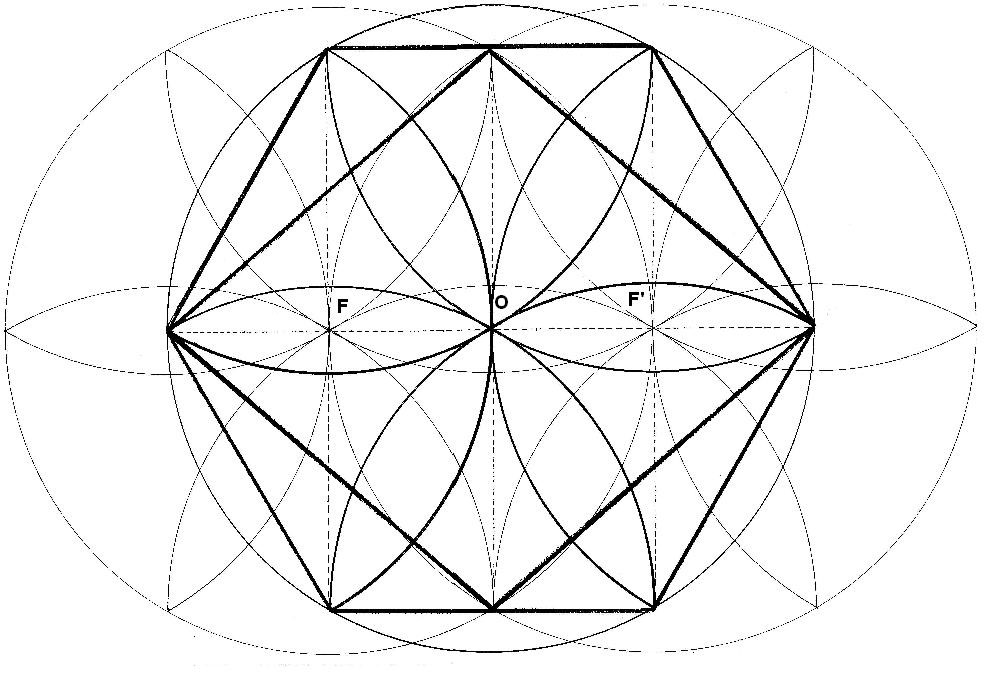
Figura. Las margaritas están en el centro y los focos

Hemos tomado 4 Rombos que aparecen formando un mosaico y obtenemos un Rombo mayor que los demás, con sus mismas proporciones. Si observamos los puntos centrales de las margaritas, obtendremos una figura que nos perseguirá continuamente en este ejercicio de dibujo. Se trata de un hexágono inscrito dentro del Rombo y que nos aportará datos muy curiosos. Vemos en este dibujo una margarita interior, y cada uno de sus vértices es un punto vital para la geometría del Rombo.

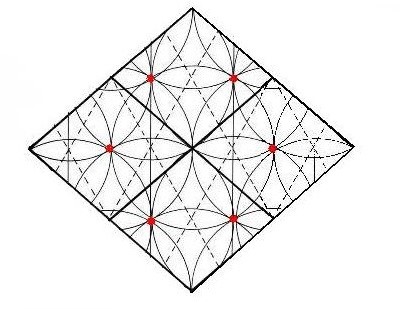
Figura. Mosaico de cuatro Rombos juntos y sus margaritas

Hacemos las 6 rotaciones posibles del Rombo dentro del hexágono (R1, R2, R3, R4, R5 Y R6). Se obtienen 3 Rombos. (Rojo, verde, azul). En cada posición del Rombo, obtenemos los dos focos ya conocidos. Al final obtenemos 6 focos que forman un hexágono interior. Dentro de este hexágono, a su vez, volvemos a obtener otro más pequeño, (Marcado con los números 1-6)

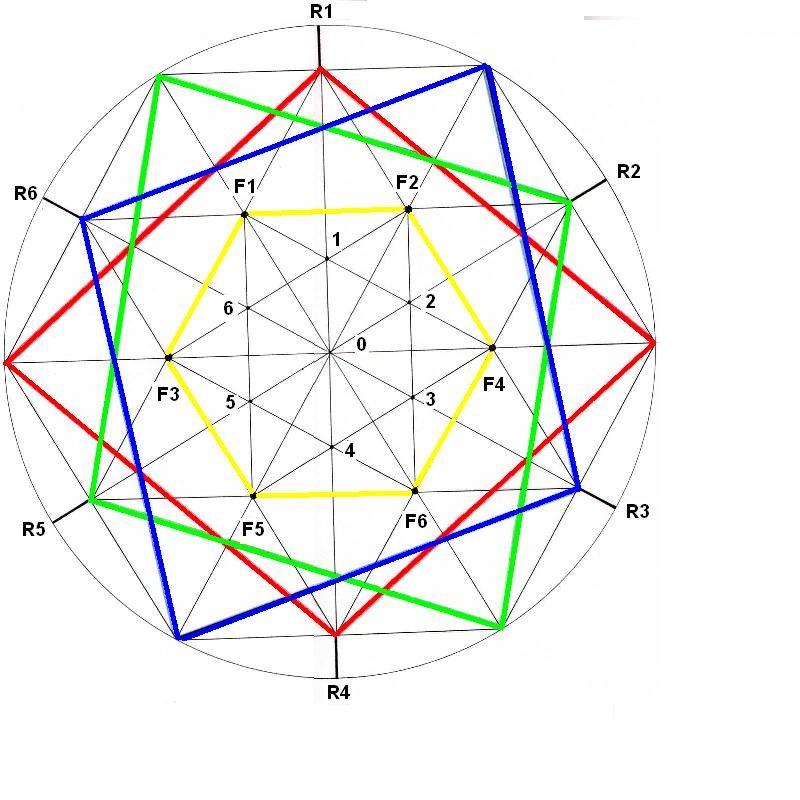
Figura. La Rotación del Rombo y el hexágono interior

Este hexágono interior, como veremos, puede aparecer muchas veces y con distintos ejercicios de geometría. En este caso, se hace patente al hacer semicírculos desde los puntos medios de los lados del hexágono exterior. (Desde los puntos 1, 2, 3, 4, 5, 6)

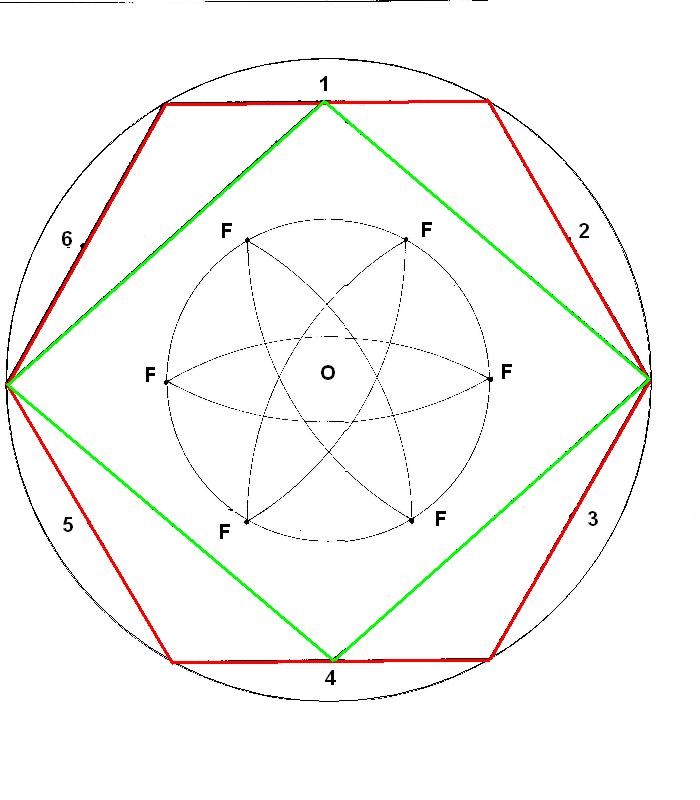
Figura. El hexágono interior del Rombo

Otro modo de obtener estos 6 focos es uniendo algunos puntos del hexágono. Unimos los vértices del hexágono y nos aparecen los seis focos. Si desde cada punto de este hexágono interior, y con radio 5´5 cm. es decir el foco, trazamos circunferencias, obtenemos puntos de corte en el Rombo. Estas intersecciones de las circunferencias y el Rombo se dan con simetría arriba-abajo, y si las unimos, aparecen las dimensiones. Aparecían las siete dimensiones, no por azar, sino por la misma construcción geométrica de la figura. Las dimensiones, se muestran como un resultado inherente a la geometría interna del rombo. Los focos, que son la excentricidad del centro, construyen las dimensiones.

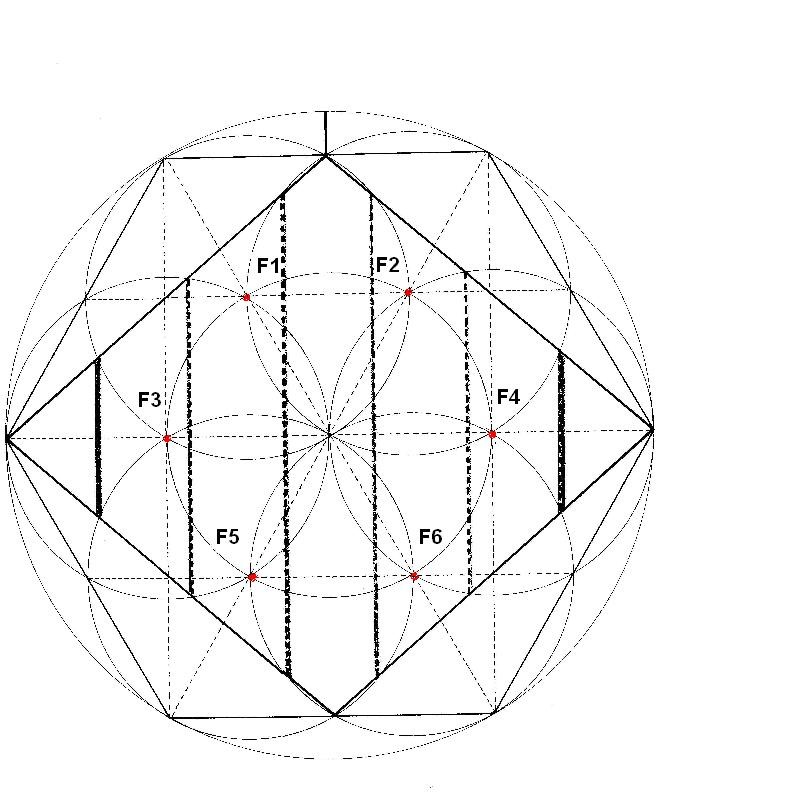
Figura. Los Focos originan las dimensiones del Rombo

En el dibujo de la izquierda aparecen unas líneas horizontales. Si dibujamos un Rombo amarillo interior al Rombo verde, las líneas horizontales se convierten en verticales y marcan los focos

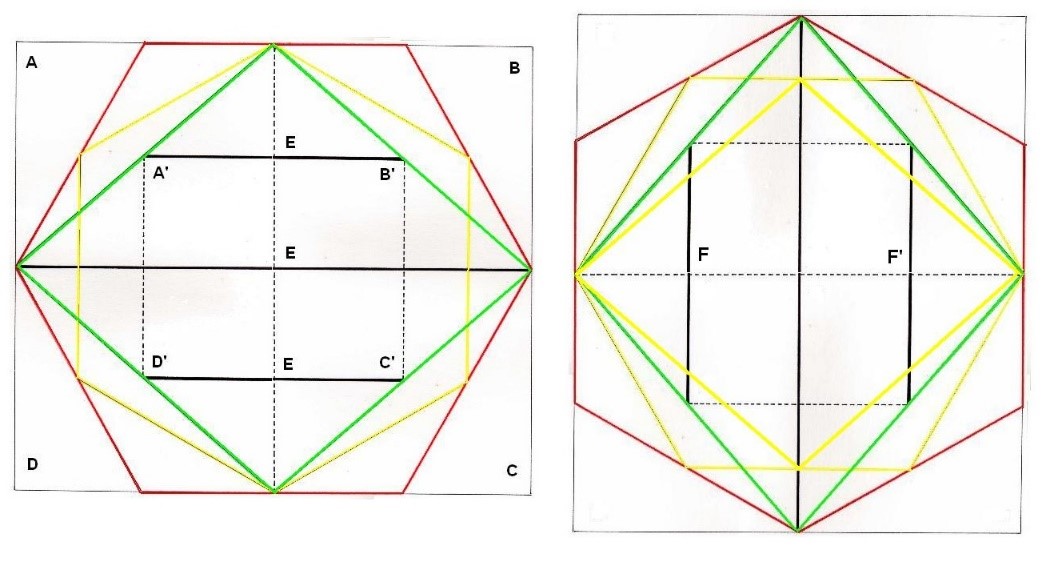
Figura. El rectángulo dentro del Rombo

El hexágono permite construir en su interior dos triángulos equiláteros muy interesantes. Si miramos un triángulo A, B, C, veremos que uno de sus lados, formará un foco F del Rombo. El otro foco, F’, lo hará el otro triángulo. Desde el punto central del triángulo, salen tres rectas de 11 cm. que forman las aristas de la figura tridimensional. El lado del triángulo (19.05) será, visto desde arriba, la diagonal menor del Rombo tridimensional. Desde el punto central del triángulo, salen tres rectas de 11 cm. que formarán las aristas de la figura tridimensional. Resulta interesante ver que dentro del mismo hexágono que permite construir el Rombo bidimensional, están las claves para hacer lo propio con el Rombo tridimensional.

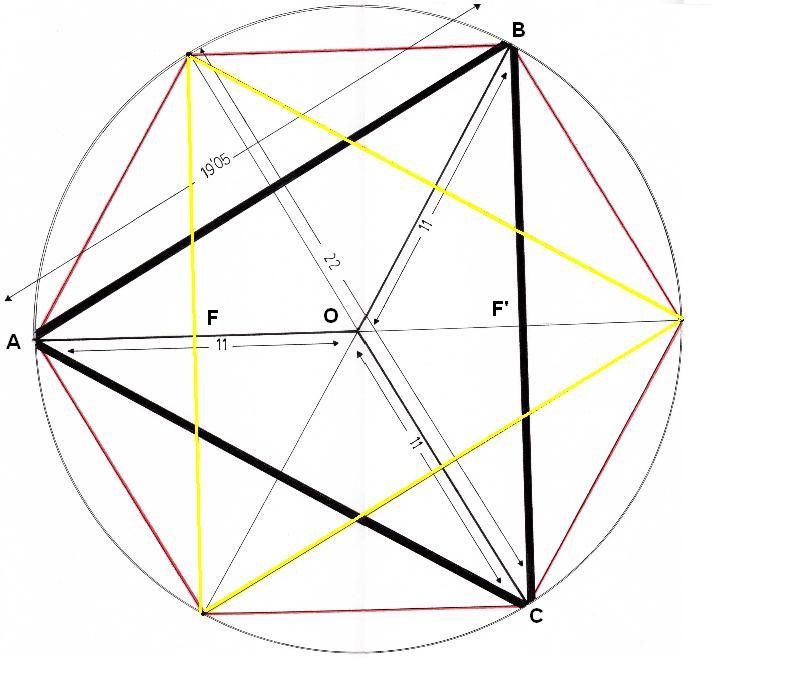
Figura. Esbozos de la figura tridimensional

Este dibujo de hexágonos interiores pone de manifiesto una relación matemática entre la Diagonal mayor y la diagonal menor del Rombo. Desde el primer hexágono (negro), se dibuja el Rombo. En el segundo hexágono (azul) se vuelve a dibujar. Vemos que la diagonal menor del primero es la diagonal mayor del segundo. Vemos también que el factor de crecimiento presente entre los hexágonos es igual a la misma relación que existe entre las diagonales, mayor y menor del Rombo.

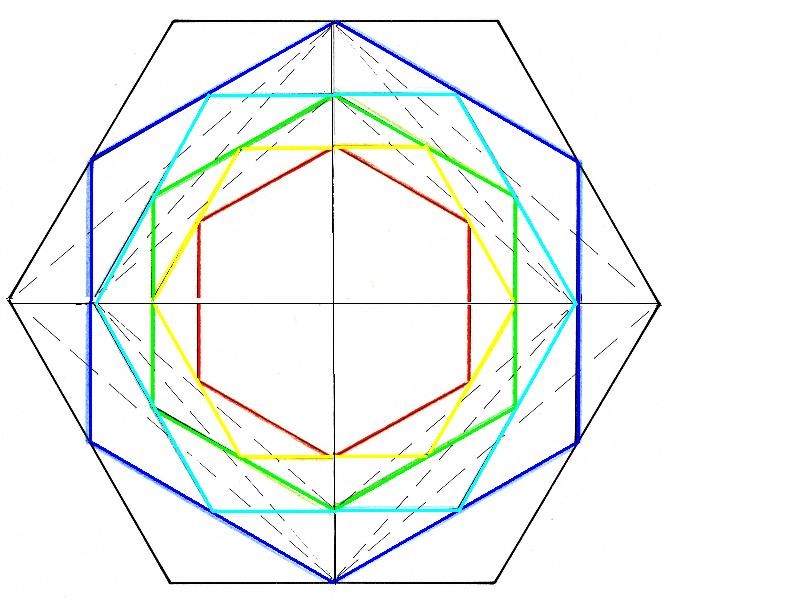
Figura. Las diagonales se transmutan al rotar 90º y varían según una constante

Un sencillo cálculo matemático nos puede dar la relación existente entre las dos diagonales. Sabemos que la Diagonal mayor = 22 y que la diagonal menor = 19.05255887. Si las relacionamos, veremos que existe una razón matemática entre ellas.

D = d ____ Factor de expansión = 1.154700539

√ 3

d = D ____ Factor de contracción = 0.866025403

Vemos los 5 Rombos interiores con sus hexágonos correspondientes. Desde las 12 posiciones exteriores hacemos círculos. También los realizamos en el interior, desde los 6 focos conocidos y desde los 4 vértices de cada Rombo menor. Cuando las circunferencias cortan los ejes horizontales, se originan diversas líneas de foco.

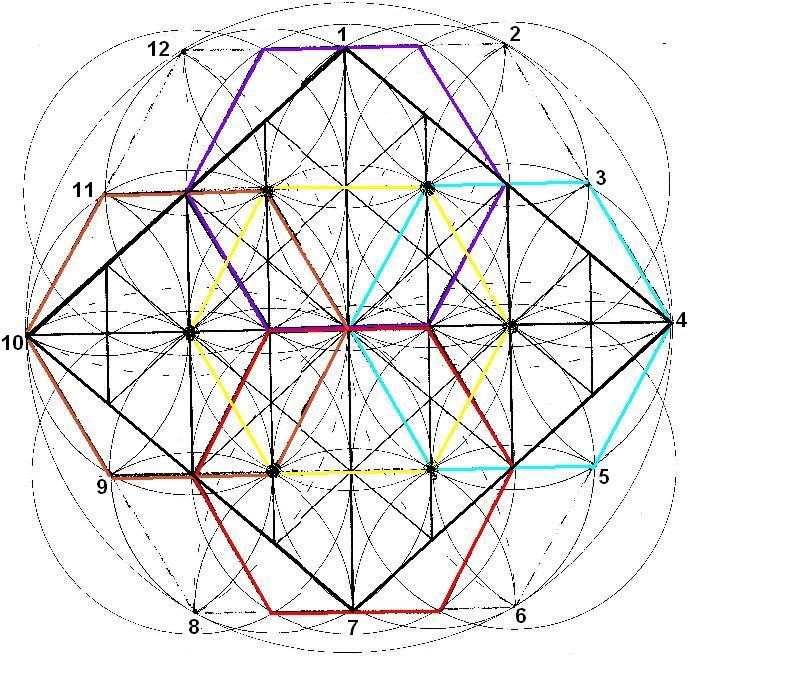
Figura. 5 hexágonos y 5 Rombos interiores

Trazamos semicírculos desde los 12 puntos exteriores, desde los 6 focos y desde los vértices de los pequeños rectángulos interiores. Es interesante observar las tres líneas horizontales que forman estas trenzas y que nos vuelven a remarcar estos ejes horizontales del rectángulo interior. Dentro de las trenzas, que son los caminos de la energía del foco, se ven líneas rectas y caminos semicirculares. Parece que la energía pueda correr en línea recta o siguiendo las funciones senoidales típicas de la radiación electromagnética

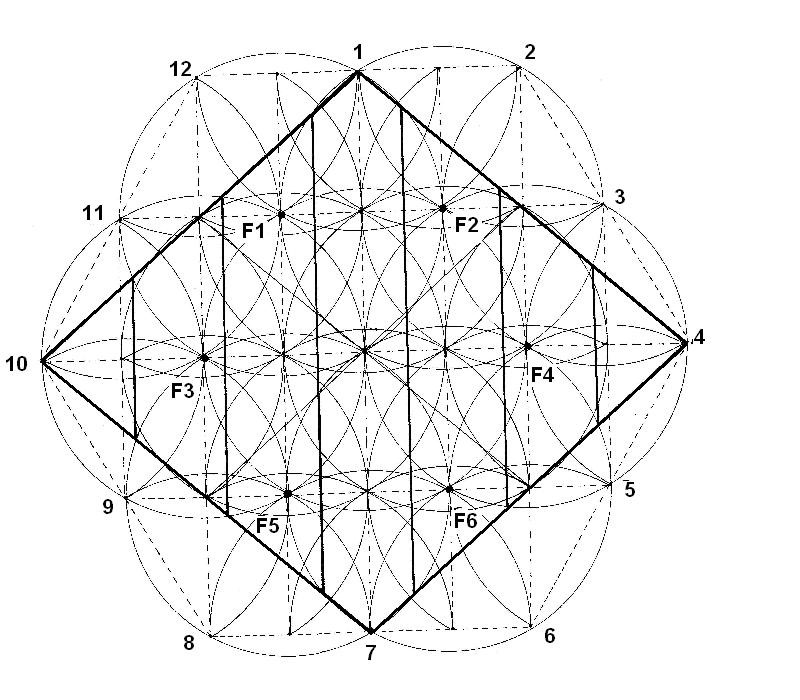
Figura. Las trenzas horizontales

Volvemos a estudiar las líneas de foco. Debe haber un número infinito de líneas de foco y estas deben ser las principales. Los puntos marcados dentro de las líneas tocan en algún punto las líneas de foco cuando estas se unen al Rombo. Se sigue entreviendo la estructura rectangular interna.

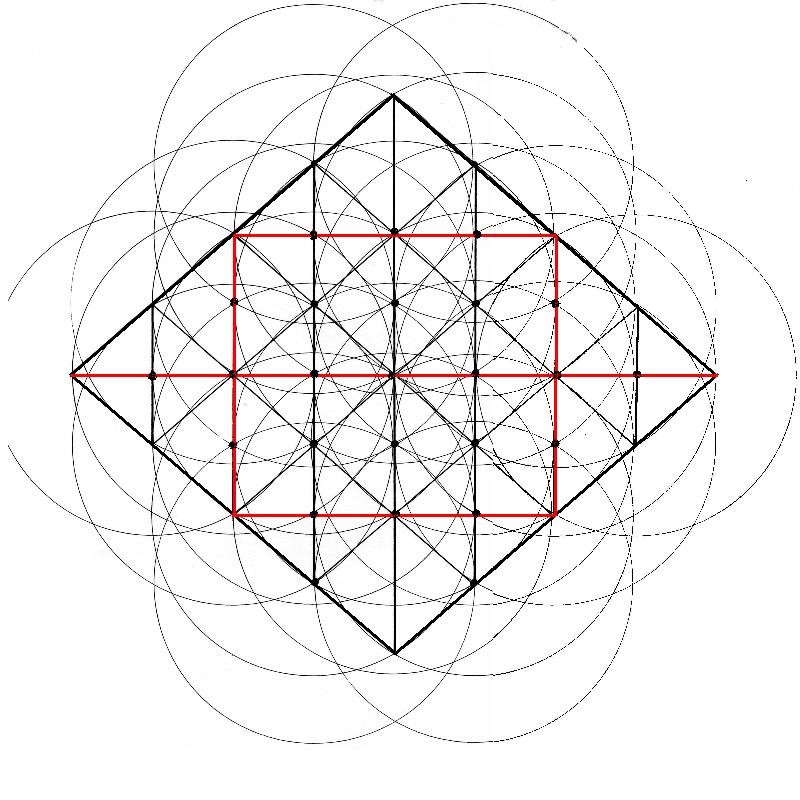
Figura. El rectángulo en la estructura interna

Dibujamos el rectángulo que enmarca al hexágono exterior. Vemos el rectángulo interior, con su hexágono y Rombo interior. Construimos las relaciones más importantes desde el rectángulo exterior. Notamos como aparecen en el Rombo interior todos los focos y el hexágono

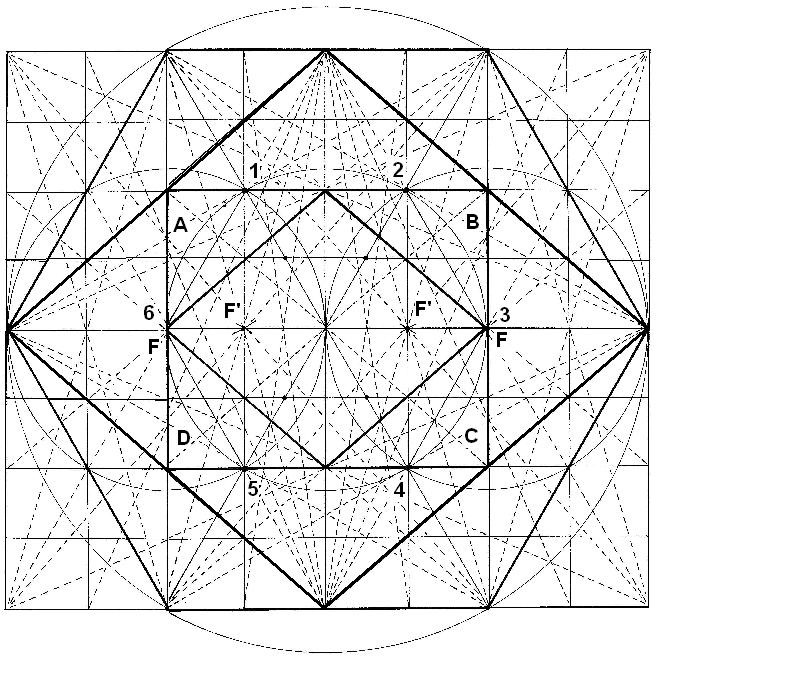
Figura. Hexágono, rectángulo y Rombo interior

Al acabar esta primera serie de dibujos, comprendimos la maravilla de la geometría interna del Rombo. Habíamos visto la posición y el valor construccional de los focos, el origen geométrico de las dimensiones, la relación entre las diagonales, la construcción del hexágono interior, las señales para la construcción de la figura tridimensional y un tamaño concreto para la línea de la ID. Como consecuencia de todo esto trabajo, se empezaron a levantar las dudas acerca de los valores de la diagonal menor y vimos que ésta podía medir sin ningún problema 19.05… este dato geométrico fue la puerta que permitió más adelante y en otros estudios posteriores desvelar un dato fundamental: La diagonal menor podía oscilar entre 18 y 19.999999 cm. lo que hacía posible que el Rombo pulsara rítmicamente del mismo modo que lo hace la vida, ya que esta, en su latir, en su pulsar continuo oscila armónicamente entre unos valores determinados.

Después de realizar esta primera serie de dibujos y desvelar la cuestión fundamental que habíamos querido encontrar, comprendimos que el resto de los dibujos que se hicieron algo posteriormente, habían perdido su valor esencial, pero en cambio estaban allí y podían hablarnos de algunos aspectos de la geometría sagrada que ignorábamos en aquellos momentos o quizá tan sólo representaban pequeños ejercicios de geometría. El tema quedó aparcado temporalmente y luego pensamos que era mejor exponerlos porque quizá en un futuro, podrían aportar nuevos datos.

El hexágono interior se puede encontrar por las bisectrices del hexágono exterior. También se puede hallar a partir de los puntos medios del hexágono exterior. Incluso desde las aristas del hexágono exterior, o desde la rotación del Rombo tridimensional visto desde arriba, y que está representado por triángulos equiláteros

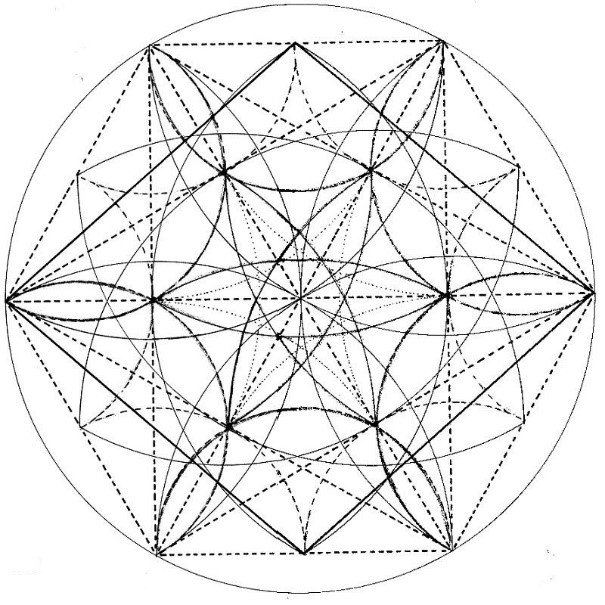
Figura. La estrella de mar

Creación del hexágono interior. Se puede conseguir desde el hexágono exterior y desde los triángulos que forma el rombo tridimensional visto desde arriba. Se observan también los ejes horizontales. Se construyen hexágonos concéntricos donde se puede construir el Rombo. Puede proporcionar una imagen de rombos concéntricos, crecientes o decrecientes.

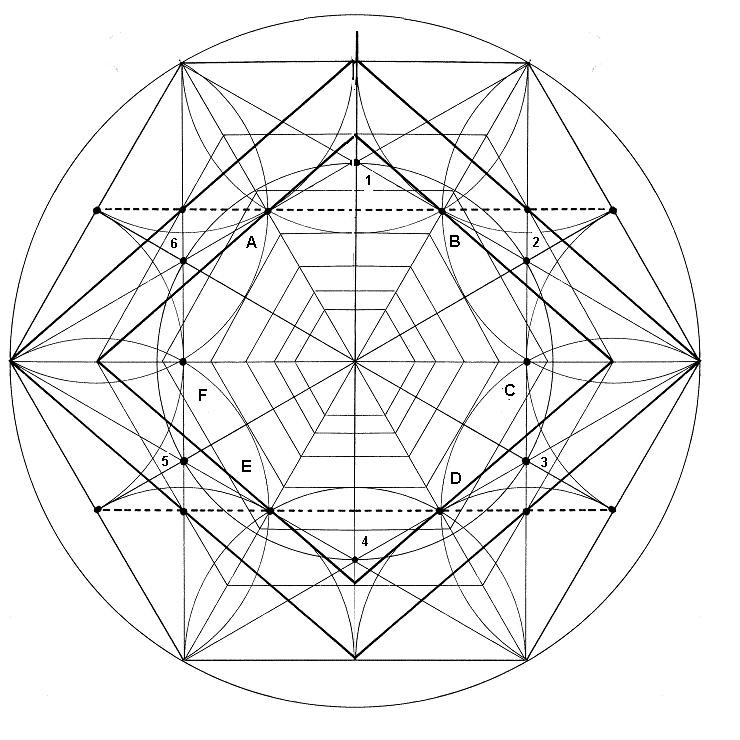
Figura. Hexágonos concéntricos

El color, intenta dar una idea de profundidad. A lo lejos, se ve el hexágono rojo, dentro del cual se puede dibujar un Rombo pequeño. A partir de aquí, por un crecimiento progresivo, se van desarrollando Rombos cada vez mayores, donde el más grande, abarca las informaciones de los más pequeños.

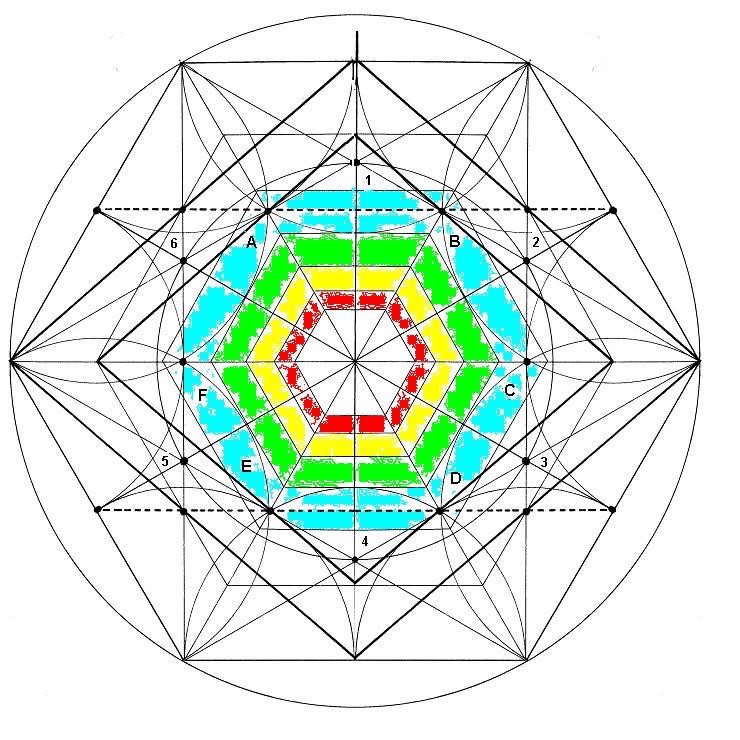
Figura. Hexágonos concéntricos con color

Desde las aristas del hexágono exterior, se marcan los puntos centrales de cada dimensión. Recordemos que los límites de cada dimensión se encontraban gracias a los focos, que están situados en las puntas de la margarita central. Es curioso observar que se puede encontrar por este sistema el punto medio de cada dimensión, a excepción de la primera y de la séptima.

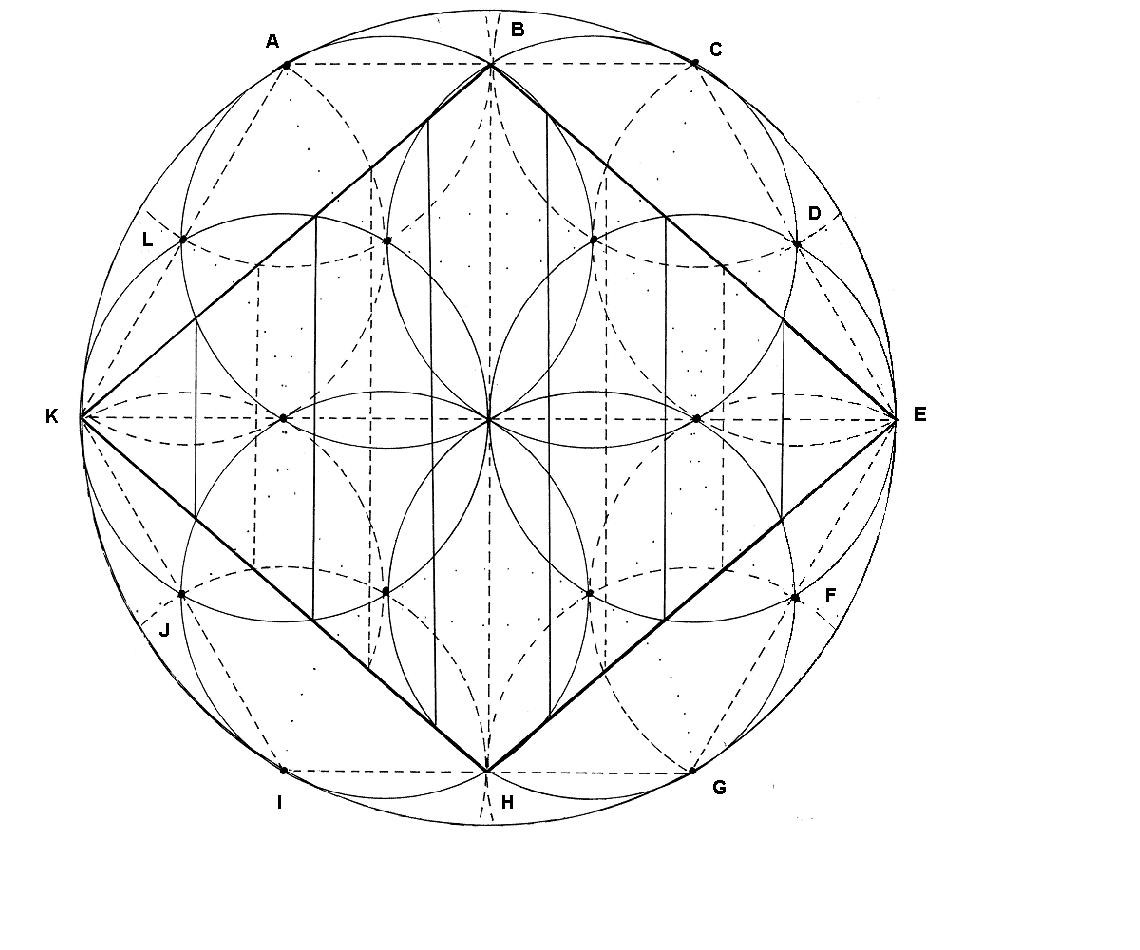
Figura. Los puntos medios de las dimensiones

No lo parece, pero es la figura anterior coloreada. Las margaritas están ya muy vistas, pero esta nueva flor de seis pétalos, con cierto aire oriental, ya no tanto. Las margaritas, nacen de la conjunción de dos pétalos consecutivos de la flor.

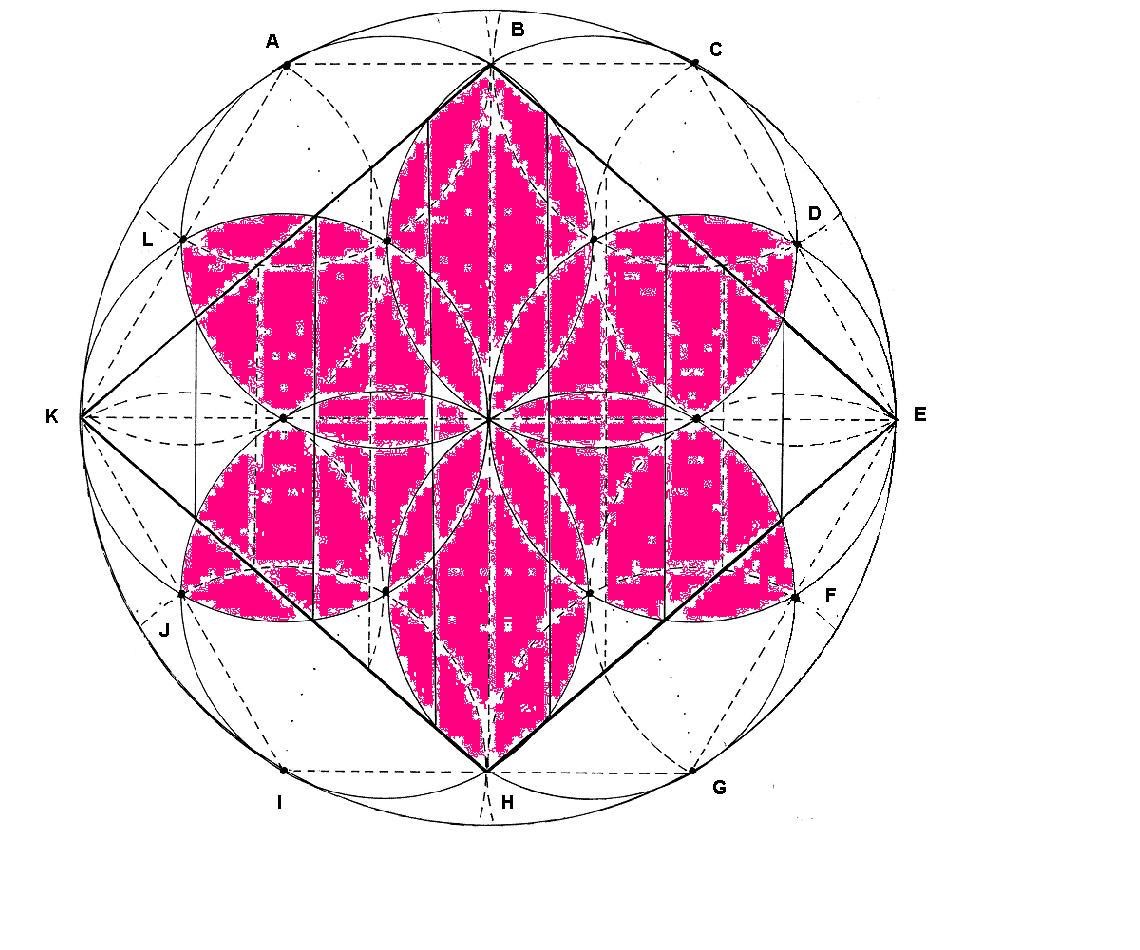
Figura. Los puntos medios de las dimensiones con color

Tenemos por fuera el hexágono ABCDEF, con sus aristas 123456. Dentro, observamos el hexágono interior hallado desde el punto central de los lados del hexágono. Se ven también los triángulos 135 y 246, que son las dos representaciones desde arriba del Rombo tridimensional. Observamos también como el hexágono interior se puede construir desde los vértices de los triángulos equiláteros 135 y 246. En el centro aparece una figura que parece un cometa o un timón

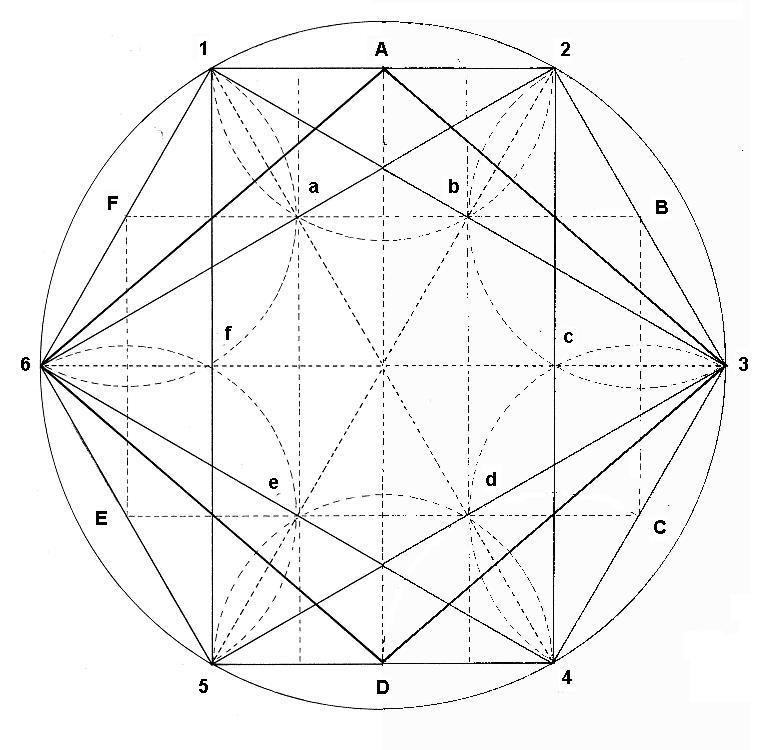
Figura. El timón

En la figura siguiente, veremos a la figura anterior coloreada de amarillo. Al pintarla de amarillo, se aprecia mejor la forma de timón o de cometa interior

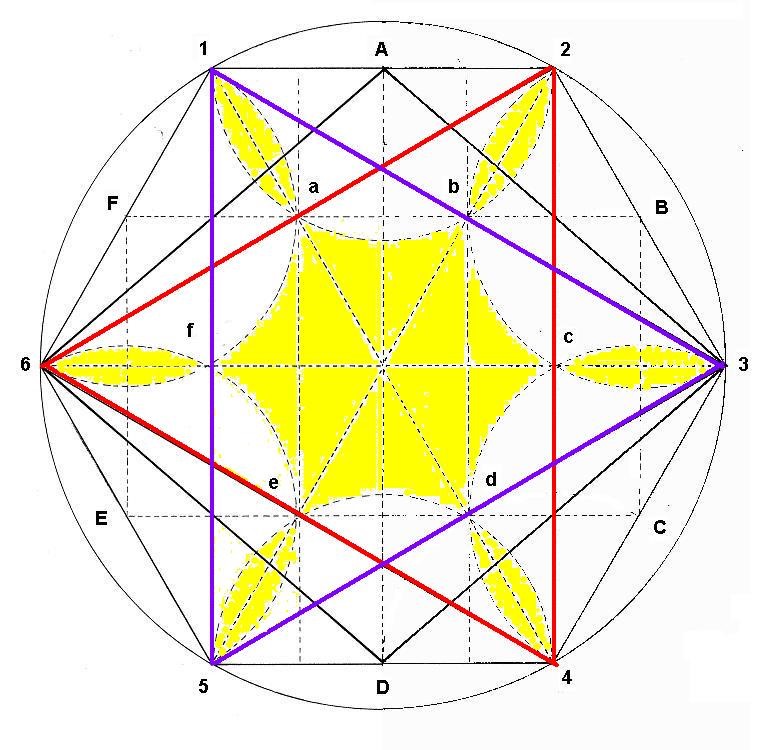
Figura. El timón coloreado

Dentro del hexágono, caben tres rombos posibles. Sus 6 focos son los vértices de las margaritas. Se observa cómo se comparten muchos puntos de límites de las dimensiones. En la figura en color, se observa con más detalle.

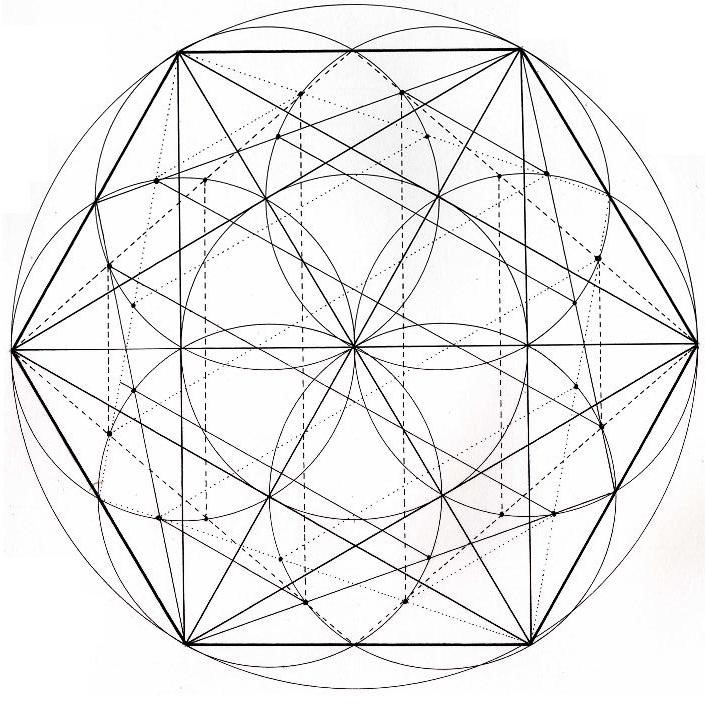
Figura. Los tres Rombos posibles

En rojo, verde y azul, los tres Rombos posibles. Si lo observamos con detenimiento, veremos que algunas líneas que marcan las dimensiones de un Rombo, están uniendo líneas de dimensiones de los otros dos Rombos. Los tres Rombos parece que están interconectados y se mantienen. Si miramos bien, también aparecerá la flor oriental de 6 pétalos. Cada uno de los pétalos, acaba en la 4ª D.

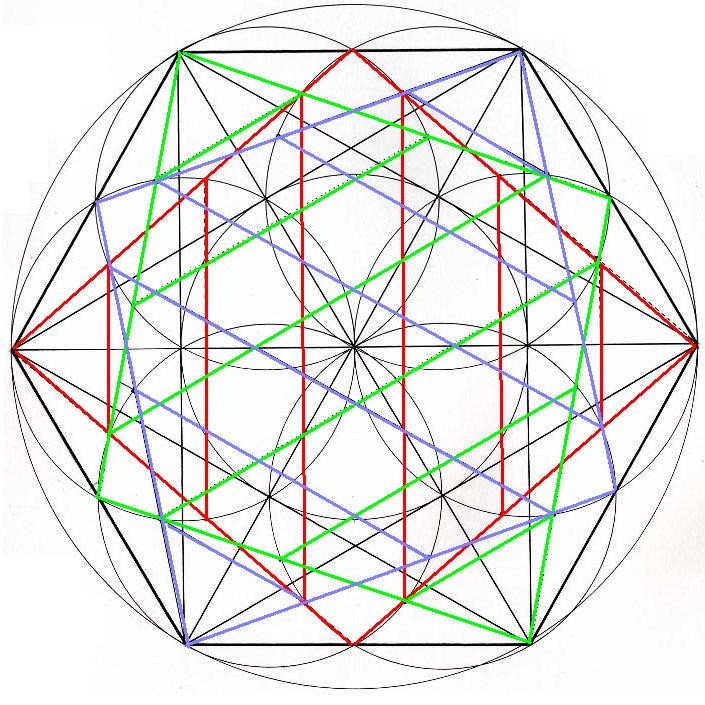
Figura. Los tres Rombos posibles coloreados

EL NUMERO ɸ EN EL ROMBO

Si el Rombo y en especial la figura con la que estábamos trabajando desde el inicio de las investigaciones, la de diagonal menor de 19,05…era armónica, y estaba relacionada con el universo, con la creación de los reinos de la naturaleza y con la evolución, el número ɸ debía estar presente en algún punto de la construcción de la figura. Pero para hallarlo, estaría bien que recordáramos como se originaba el número áurico y a partir de aquí, quizás podíamos hallarlo en el Rombo.

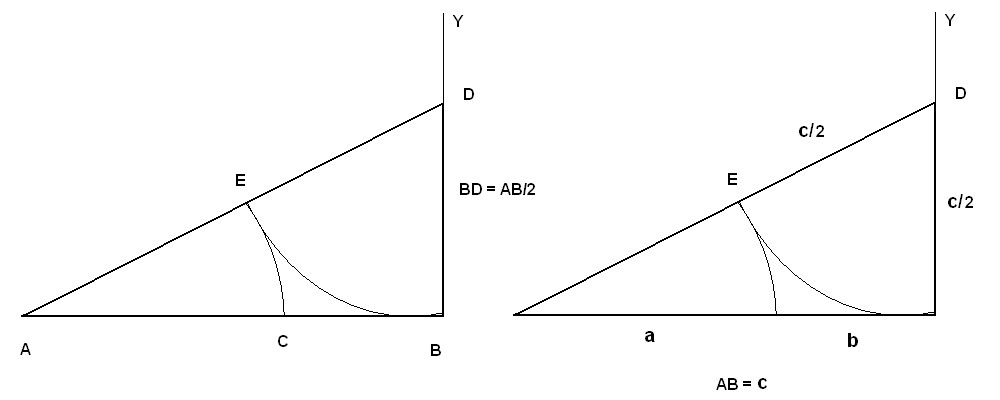
Figura. Origen del número áurico

Dibujamos la línea AB y proyectamos sobre BY otra línea de manera que BD sea la mitad de AB, con lo que BD = AB/2. Con un compás desde el punto D, hacemos un semicírculo BE. Desde A, realizamos otro semicírculo a partir del punto E. Nos queda la línea inferior del triángulo dividida en dos partes: El segmento AC (le llamaremos a), y el segmento CB (le llamaremos b). La suma de los dos trozos de la recta es la línea AB (a la que llamaremos c = a+b)

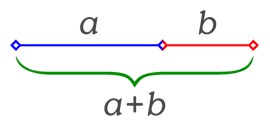
Tenemos un segmento c dividido en dos partes, a y b, de forma que la razón entre la totalidad del segmento y la parte a sea igual a la razón entre la parte a y la parte b.

Expresado matemáticamente:

A esta razón, que cumple la propiedad, se le denomina razón o número áureos.

Podemos obtener matemáticamente este número a partir de la resolución de la ecuación anterior:

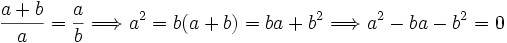
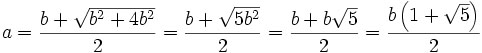
Dividiendo todo por b obtenemos:

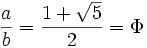
ɸ =1.618...

Aquí tenemos el nacimiento de una proporción y el del número. ɸ Nuestro objetivo era observar si en el Rombo en el que hemos estado trabajando, el de 19.05 de diagonal menor, aparecía esta razón áurea. Estaba claro que para poder encontrar a ɸ en el Rombo, teníamos que mirar atentamente a estos dos segmentos: a y b. Si eran tan importantes, posiblemente, todo el Rombo tenía que estar relacionado con el segmento a y también con el segmento b. Para verificar la hipótesis, teníamos que buscar si dentro de la construcción del Rombo, podíamos colocar en alguna zona, a estos dos segmentos. Pensamos que una de las posibles maneras de encontrar algo, era colocar directamente el triángulo áurico dentro del Rombo y ver que sucedía.

De entrada, observamos que el triángulo podía tener cabida física dentro del Rombo. Una vez colocado el triángulo en el Rombo, observamos el resultado y vimos que aparecían dos cosas que nos gustaban. Por un lado, el cateto mayor del triángulo del estudio podía situarse perfectamente sobre la parte izquierda de la diagonal mayor. El cateto mayor del triángulo rectángulo tendría 11 cm. y el cateto menor, y por construcción, justo la mitad de esa cifra, es decir 5,5 cm, y arrancaría desde el punto Hara del Rombo, siguiendo el trayecto ascendente de la diagonal menor.

Ambas cifras, sonaban muy bien, pues el número 11 es la mitad de 22 (Diagonal mayor) y 5.5 también, ya que es la distancia a la que se halla el foco desde el punto central del Rombo. Así que, siendo dos cifras muy importantes en la construcción de la figura del Rombo, había algo que, en principio, resultaba estético, parecía que otorgaba algunas posibilidades y con un poco de suerte, quizás podría encontrar algunas relaciones.

Para poder encontrar a ɸ , teníamos que mirar y estudiar mucho a los dos segmentos que originan la relación: a y b. Así que lo primero, fue transformar un concepto, una ecuación de ɸ, en números reales y concretos con los que poder trabajar matemáticamente y constatar las realidades acerca de las suposiciones.

CALCULANDO LOS VALORES NUMERICOS DEL TRIANGULO

Como si se tratara de un problema elemental de geometría, vamos a encontrar gracias al cálculo Pitagórico, los valores de este triángulo rectángulo.

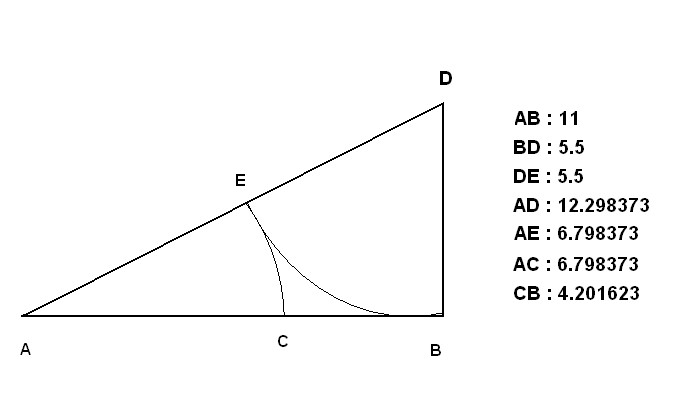
Figura. El triángulo áurico y sus medidas

__________

AD = √AB ²+ BD²

___________

AD = √ 121 +30.25

_______

AD = √ 151.25

AD = 12.298373

AE = AD – DE

AE = 12.298373 – 5.5

AE = 6.798373

AC = AE

AC = 6.798373

BC = AB - AC

BC = 11- 6.798373 = 4.201627

Estas cifras son las que nos ayudarán posteriormente a realizar cualquier tipo de comprobación que queramos hacer acerca de los resultados que hallemos. De esta forma, verificaremos si las conclusiones a las que llegamos bajo la forma de ecuaciones son correctas o no. Son cifras importantes y las deberemos mirar a menudo para saber si nuestras conclusiones matemáticas son exactas. Pasaremos ahora a estudiar las relaciones de las distintas partes constituyentes del Rombo con los dos segmentos AC (a) y BC (b) para ver de qué tipo son las relaciones encontradas.

COLOCACION DEL TRIANGULO AURICO DENTRO DEL ROMBO

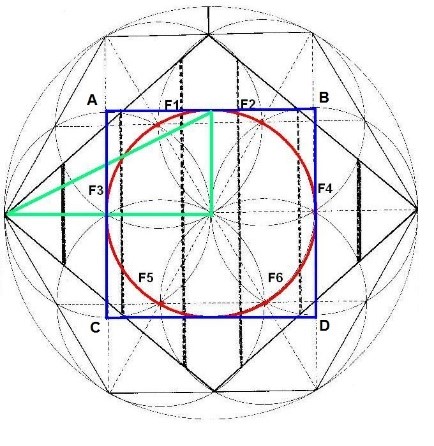
Figura. En color verde, observamos el triángulo áurico.

Vemos en la parte más exterior del dibujo, la circunferencia madre, hecha con un radio de 11 cm. origen a su vez del hexágono circunscrito. Visualizamos también el Rombo con sus 7 dimensiones, halladas geométricamente a partir del Rombo y de sus intersecciones con las circunferencias interiores hechas a partir de los focos, de radio 5.5 cm. Observamos el círculo rojo, que es vital para la construcción interior del Rombo, una especie de armazón, que unifica a todos los focos. En azul, observamos el cuadrado vinculado a la circunferencia interior y que nace también por las intersecciones de la construcción interna.

Para realizar el estudio matemático que vamos a llevar a cabo, partiremos de esta figura compleja y del triángulo áurico coloreado en verde que hemos colocado en su interior. Trabajaremos sobre este triángulo, que abarca la mitad de la diagonal mayor y un trozo de la diagonal menor, concretamente el segmento que va desde el centro hasta el punto de corte con el círculo rojo. Primero, trasladaremos el triángulo y los valores buscados a una figura más sencilla. Es el mismo dibujo anterior, pero sin tanto estudio geométrico.

Sobre la Diagonal mayor del Rombo que mide 22 cm, trazamos una recta AB de 11cm. Desde el punto B, trazamos hacia arriba otra línea BD, que, por definición del triángulo áurico, ha de ser la mitad de AB. Además, sabemos también que, por construcción, en este Rombo, BD medirá 5,5 cm. justamente la misma distancia que hay desde al centro al Foco.

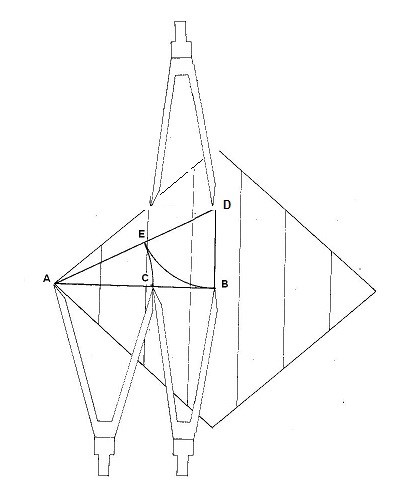
Figura. El triángulo áurico dentro del Rombo

Sigamos con la construcción de la figura. Desde el punto D, nos vamos hacia B y trazamos con un compás un semicírculo, que corta la línea AD en el punto E. Entonces, desde A, trazamos un semicírculo descendiente que partiendo desde E llega a la recta AB. En la intersección, aparece el punto C. Aplicamos la ecuación que hemos determinado anteriormente en el ejercicio algebraico y obtenemos la razón áurea que podemos seguir en la figura superior.

BC x ɸ = CA

CA x ɸ = AB

1. LA RELACION AURICA DEL FOCO

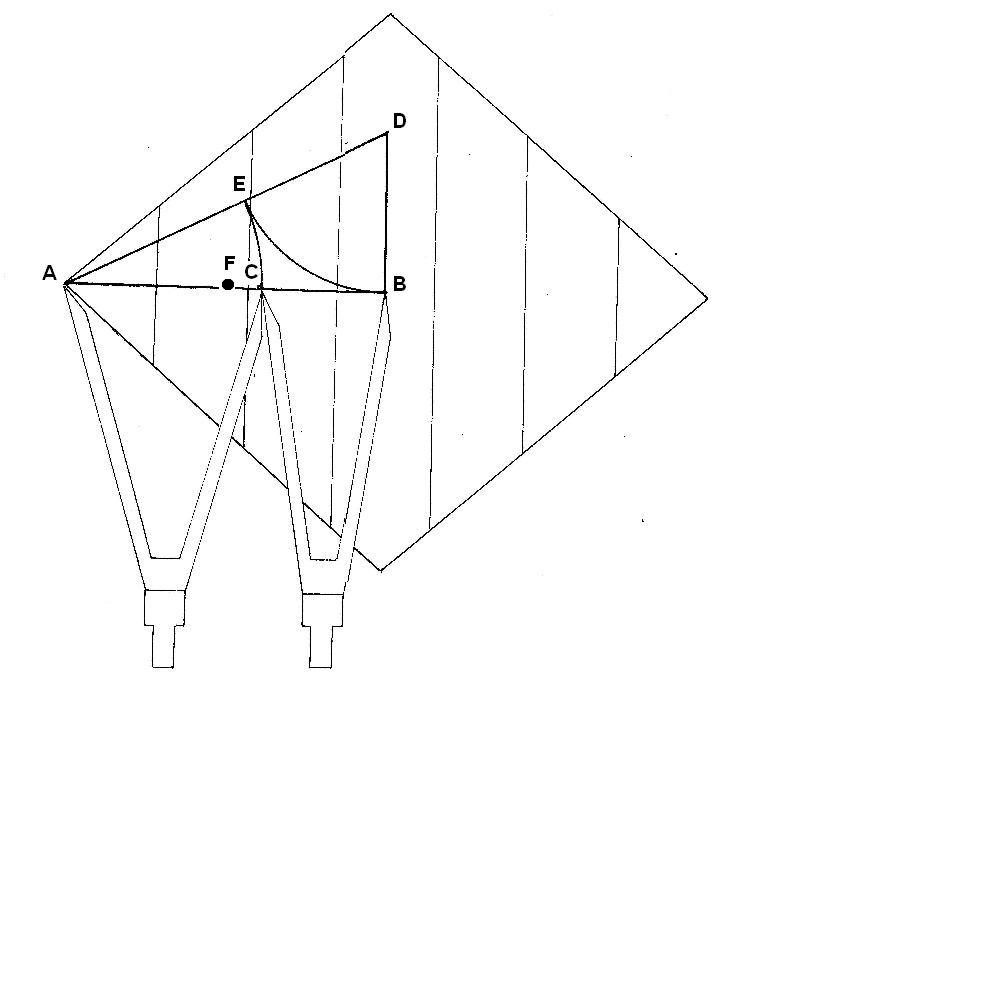
Figura. Relación áurica del Foco

Colocamos al Foco en su posición por construcción, es decir, en el centro de la línea AB. Tenemos las relaciones conocidas: BC x ɸ = AC y AC x ɸ = AB

Reemplazamos este segundo AC por el valor obtenido en la primera ecuación y podemos entonces, obviamente llegar a la conclusión que:

BC x ɸ x ɸ = AB o lo que es lo mismo BC x ɸ ² = AB

Como sabemos, el foco (5.5) es la mitad de AB (11), así que BC x ɸ ² = 2F

F = BC x ɸ ²

Sabemos que AB = AC x ɸ. Como que AB = 2F, sustituimos

2F = AC x ɸ Con lo que obtenemos F

F = AC x ɸ

Que son las razones áuricas entre el Foco y los segmentos. Este es un dato muy importante, porque el foco es el punto de equilibrio y de construcción de toda la figura. El foco guarda una relación áurica con los segmentos originales.

COMPROBACION DE LA RELACION AURICA DEL FOCO

F = AC x ɸ

Reemplazamos por los valores conocidos:

AC = 6.798373

ɸ = 1.618033

F = 6.798373 x 1.618033 = 5.5

Miramos ahora la otra fórmula:

F = BC x ɸ ²

Reemplazamos por los valores conocidos:

BC = 4.201627

ɸ = 1.618033

F = 4.201627 x 1.61803 ² = 5.5

2. LA RELACION AURICA DE LA DIAGONAL MAYOR

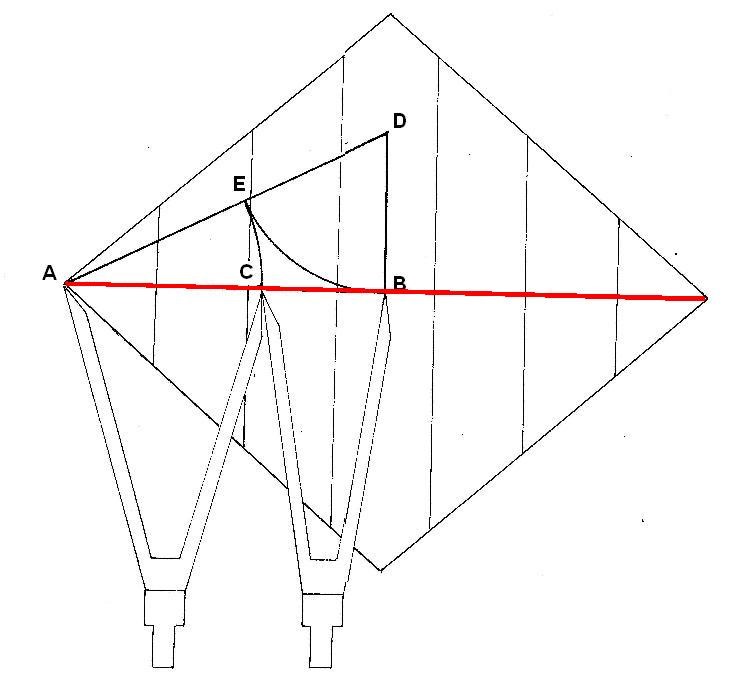
Figura. Relación áurica de la Diagonal mayor

Sabemos por construcción que 4F = Diagonal mayor, así que

D = 4F Reemplazando el valor de foco hallado anteriormente

D = 4 BC x ɸ ² o lo que es lo mismo

D = BC x 2 ɸ²

De igual manera, para obtener la otra relación, reemplazamos por el otro valor del Foco obtenido antes.

D = 4F

D = 4 AC x ɸ o lo que es lo mismo

D = AC x 2 ɸ

Lo que nos dice que la Diagonal Mayor del Rombo, está en relación áurica con los segmentos.

COMPROBACION DE LA RELACION AURICA DE LA DIAGONAL MAYOR

D = AC x 2F

Reemplazamos por los valores hallados:

AC = 6.798373

F = 1.618033

D = 6.798373 x 2 x 1.618033 = 22

D = BC x 2 ɸ²

Reemplazamos por las cifras conocidas

BC = 4.201627

ɸ = 1.618033

D = 4.201627 x 2 x 1.618033 ² = 22

3. LA RELACION AURICA DE LA DIAGONAL MENOR

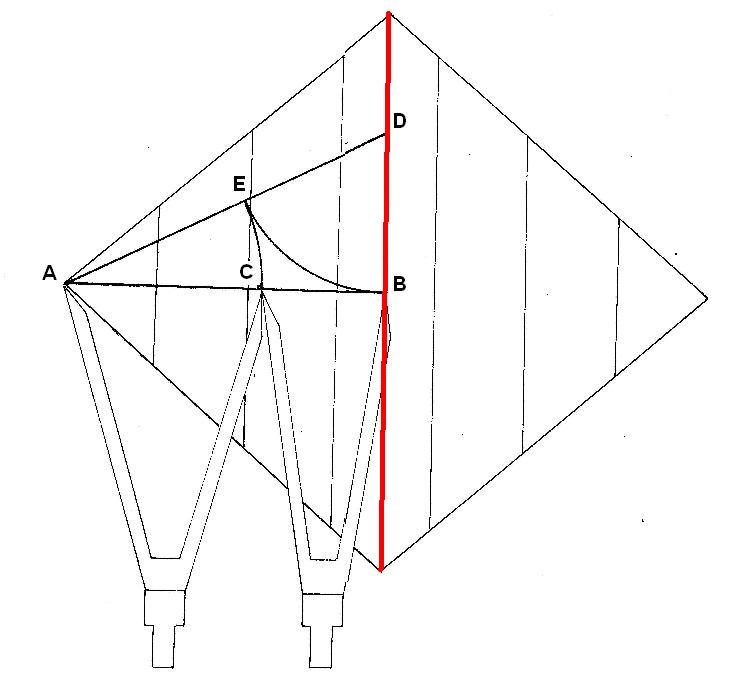
Figura. Relación áurica de la diagonal menor

Conocemos la relación matemática entre la diagonal menor y la mayor. Si lo recordamos, vemos que:

d = D √3_ substituimos el valor hallado de D y obtenemos

d = AC √3 ɸ

d = 2AC x ɸ √3

Si buscamos la relación con el segmento BC, obtendremos lo siguiente:

d = D √3_ substituyendo el valor hallado para D obtenemos

d = BC √3 ɸ ²

d = BC x 2ɸ ² x √3

Por lo que encontramos la relación áurica en la diagonal menor.

COMPROBACION DE LA RELACION AURICA DE LA DIAGONAL MENOR

Habíamos visto en el anterior artículo que la diagonal menor medía 19.05

Comprobaremos ahora este valor con el hallado con la relación áurica:

d = AC √3 ɸ

d = 6.798373 √3 ɸ = 19.05

Para el otro segmento:

d = BC √3 ɸ ²

d = 4.201627 √3 ɸ ² = 19.05

4. LA RELACION AURICA DEL LADO DEL ROMBO

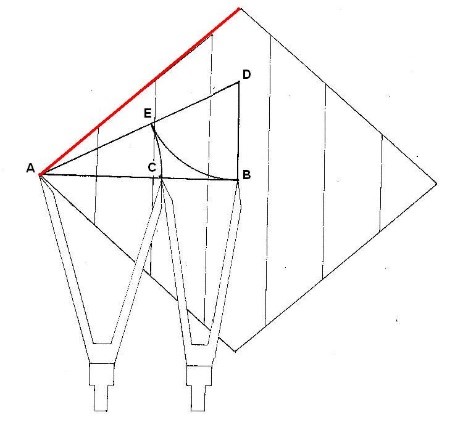
Figura. La relación áurica del lado del Rombo

Partimos de un triángulo del que conocemos los dos catetos (Media Diagonal mayor y media diagonal menor) Hallaremos la hipotenusa que es el lado del Rombo marcado en rojo.

H ² = C ² + C ²

__________________________

h = √ ( AC √3 ɸ/2) ² + ( AC ɸ) ²

√ 7

h = AC ____ ɸ

Ahora, repetiremos el cálculo para el otro segmento, el BC.

H ² = C ² + C ²

______________________________

h = √ ( BC √3 /2 ɸ ² ) ² + ( BC ɸ ²) ²

√7

h = BC ____ ɸ ²

Por lo que también vemos la relación áurica en los lados del Rombo.

COMPROBACION DE LA RELACION AURICA DEL LADO DEL ROMBO

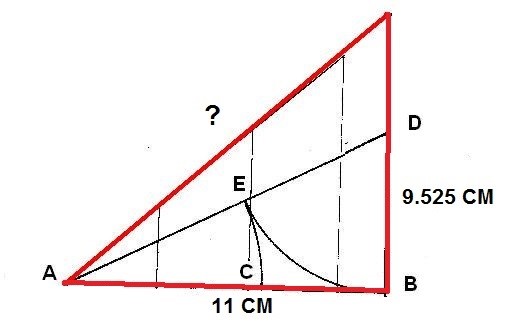
Figura. Comprobación de la relación áurica del lado del Rombo

Observamos en detalle el lado del Rombo que queremos estudiar. Conocemos los dos catetos y buscamos el valor de la hipotenusa.

__________________

h = √ ( 11 ) ² + ( 9.525)²

_____________

h = √ 121 + 90.725

h = 14.5

Reemplazamos los valores obtenidos:

√ 7

h = AC ____ ɸ

√ 7

h = 6.79 ____ ɸ = 6.79 x 2.645 x ɸ = 14.5

2 2

√7

h = BC ____ F ²

√ 7

h = 4.20 ____ ɸ² = 4.20 x 2.645 x ɸ² = 14.5

2 2

Por lo que también vemos la relación áurica en los lados del Rombo.

5. RELACIONES AURICAS DE LAS LINEAS INTERDIMENSIONALES

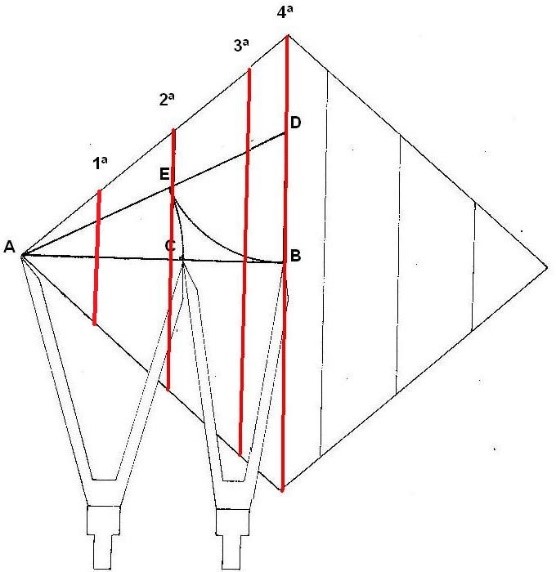
Figura. Relaciones áuricas inter dimensionales

El desarrollo algebraico de todas estas operaciones, es un poco aparatoso y no tiene demasiado interés, así que solo exponemos el resultado final:

_ _

Primera línea dimensional AC 2√3 ɸ BC 2√3 ɸ²

7 7

_ _

Segunda línea dimensional AC 4√3 ɸ BC 4√3 ɸ²

7 7

_ _

Tercera línea dimensional AC 6√3 ɸ BC 6√3 ɸ²

7 7

_ _

Cuarta línea dimensional AC √3 ɸ BC √3 ɸ ²

Por lo que vemos que cada línea ínter dimensional está relacionada con Phi.

COMPROBACION DE LAS RELACIONES AURICAS DE LAS LINEAS

INTER DIMENSIONALES

Al hacer el cálculo, obtenemos los siguientes valores:

_ _

Primera línea AC 2√3 ɸ 5.44 cm BC 2√3 ɸ²

7 7

_ _

Segunda línea AC 4√3 ɸ 10.88 cm BC 4√3 ɸ²

7 7

_ _

Tercera línea AC 6√3 ɸ 16.33 cm BC 6√3 ɸ²

7 7

_ _

Cuarta línea AC √3 ɸ 19.05 cm BC √3 ɸ ²

6. RELACION AURICA DEL AREA DEL ROMBO

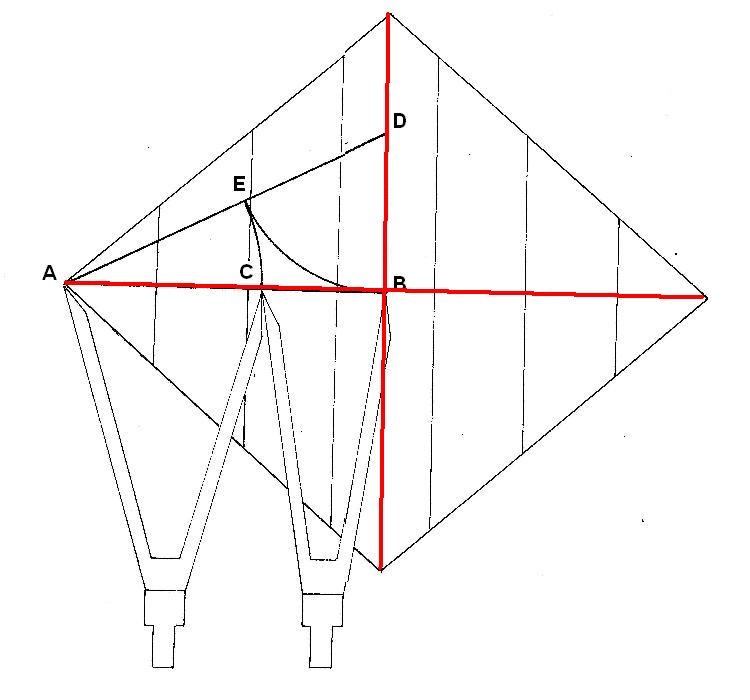
Figura. Relación áurica del área del Rombo

La fórmula del área del Rombo es

D x d

A = ____ =

Sustituimos los valores hallados

__ __

Area = (AC 2ɸ) X ( AC √3 ɸ) = AC ² √3 ɸ²

Para el otro segmento

__ __

Area= (BC 2ɸ²) x (BC√3 ɸ²) = BC ² √3 ɸ4

COMPROBACION DE LA RELACION AURICA DEL AREA DEL ROMBO

La fórmula del área del Rombo es

D x d 22 x 19.05

A = ______ = _________ = 209.5

2 2

Sustituimos los valores hallados

__ __

Area = (AC 2ɸ) X ( AC √3 ɸ) = AC ² √3 ɸ²

Área = 6.79 x 6.79 x √3 ɸ² = 209.5

Para el otro segmento

__ __

Area= (BC 2ɸ²) x (BC√3 ɸ²) = BC ² √3 ɸ4

Área = 4.20 x 4.20 √3 ɸ4 = 209.5

CONSIDERACIONES FINALES

El trabajo original del artículo era bastante más largo que este, porque incluía otros cálculos, como las relaciones áuricas de cada una de las dimensiones, pero posiblemente no venían a aportar demasiados datos nuevos, sino que, en cierta manera, eran una repetición matemática de todo lo visto hasta ahora.

En principio, después de haber realizado las primeras determinaciones matemáticas y haber visto que todo el Rombo, con sus partes primordiales, se podía construir con el segmento a y con el segmento b, podríamos dar por finalizado el estudio, ya que era evidente la presencia matemática de ɸ en toda la construcción del Rombo. Habíamos observado con los cálculos hechos, que cualquiera de estos dos segmentos, si se multiplicaba por algún factor de ɸ, originaba todo el Rombo, toda su geometría interna. Se creaban así las dimensiones, los lados, los focos, las líneas ínter dimensionales y las áreas. Todas las partes de la figura aparecían al multiplicar a o b por un factor numérico variable y por el número áureo. Si tomábamos el segmento a = 6.798373, o el segmento b = 4.201627 y lo hacíamos interactuar matemáticamente con algún factor variable y con ɸ, aparecían todos los distintos valores constituyentes del Rombo.

Todo el Rombo de 22 cm de Diagonal mayor y 19.05 cm de diagonal menor, se puede construir, por ejemplo, a partir del segmento a=6.79. Pero si por algún motivo, cambiamos, el valor inicial del segmento a por cualquier otro valor aleatorio, como por ejemplo a=1, obtendremos entonces un Rombo distinto en tamaño, pero con la misma proporción. En ese caso, la Diagonal mayor valdría D=1x2ɸ = 3.23 y el valor de la diagonal menor sería d= 1x√3ɸ = 2.80 pero la razón entre la Mayor y la menor seguirá siendo la misma: 2 / √3.

De hecho, no es la medida del Rombo lo más importante, sino la proporción entre todos sus constituyentes. Un Rombo armónico, se puede construir de cualquier tamaño, pero se ha de partir de un valor inicial determinado con el que vamos a trabajar. Este valor primario, este segmento constructor primigenio, puede ser cualquier cifra, pero si tiene el valor a = 6.798373, la Diagonal mayor, medirá 22. Con cualquier otra cifra, el valor de la Diagonal mayor será distinto, aunque el Rombo tendrá las mismas proporciones interiores y será idéntico en cuanto a leyes.

Podemos hacer un ejemplo para observar esto con más claridad. Estudiaremos el valor de las líneas ínter dimensionales con el valor inicial del segmento a = 6.798373 y luego, realizaremos el mismo cálculo, pero al segmento a, le daremos el valor de a=1. Observaremos los cálculos y veremos que los Rombos resultantes, aunque distintos en tamaño, tienen la misma proporcionalidad y razón.

COMPROBACIÓN CON LOS DISTINTOS VALORES DEL SEGMENTO a

Recordamos el ejemplo anterior en el que el valor de AC (a) era de

AC = 6.798373. Para este valor, obteníamos estas cifras:

Primera línea AC 2√3 ɸ 5.44 cm

Segunda línea AC 4√3 ɸ 10.88 cm

Tercera línea AC 6√3 ɸ 16.33 cm

Cuarta línea AC √3 ɸ 19.05 cm

Pero si dibujamos otro Rombo en el que el valor de a=1, entonces, obtendremos las siguientes cifras:

Primera línea 1 x 2√3 ɸ 0.80 cm

Segunda línea 1 x 4√3 ɸ 1.60 cm

Tercera línea 1x 6√3 ɸ 2.40 cm

Cuarta línea 1x √3 ɸ 2.80 cm

Este Rombo pequeño, mantiene las mismas razones entre sus distintos lados que las que tiene el Rombo mayor. Ambos Rombos, son distintos en tamaño, pero idénticos en proporciones. Son el mismo Rombo, pero su valor total es 6.798373 veces menor.

El valor de cada línea del Rombo, de cada área, resulta de la multiplicación del valor del segmento constructor primario, con los distintos factores de ɸ y con el mismo número ɸ .

Valor de una línea = Valor segmento constructor x Factor de ɸ x ɸ

El factor de ɸ, es el valor que multiplicará a ɸ, y será lógicamente lo que determinará las diferencias finales y las razones de los valores hallados. ɸ, es constante y está presente en todas las ecuaciones. Lo que determina realmente el valor final de las líneas, es la razón variable que multiplica a ɸ. Ese factor es siempre distinto para cada línea y es el que hará que una línea sea mayor o menor respecto a la otra, pero siempre un número racional ɸ de veces.

La idea inicial del trabajo era encontrar alguna presencia del valor ɸ en la construcción de la figura. Al final del desarrollo del ejercicio, se ha encontrado una clara relación áurica entre el segmento original constructor y todos los valores numéricos que resultan de la construcción de las distintas partes del Rombo. Todos los segmentos, todas las líneas, todas las áreas están relacionados entre ellos por un número ɸ de veces. Y este hallazgo, creo que es el punto clave del estudio. Seguramente, el contenido más importante. Creo que, con estos argumentos matemáticos, podemos decir con tranquilidad y certeza que la proporción áurea, se encuentra en todas las unidades constituyentes de la figura. El número ɸ está en todas las partes del Rombo. Allí está, agazapado, silencioso, sin apenas decir nada, inadvertido, escondido e invisible, como todo el conocimiento del Rombo. No se le observa dentro del Rombo a simple vista, pero a nuestra figura, hay que estudiarla, ver de lo que está hecha, razonarla, abrirla suavemente y entonces es cuando muestra contenta su inɸnito contenido.

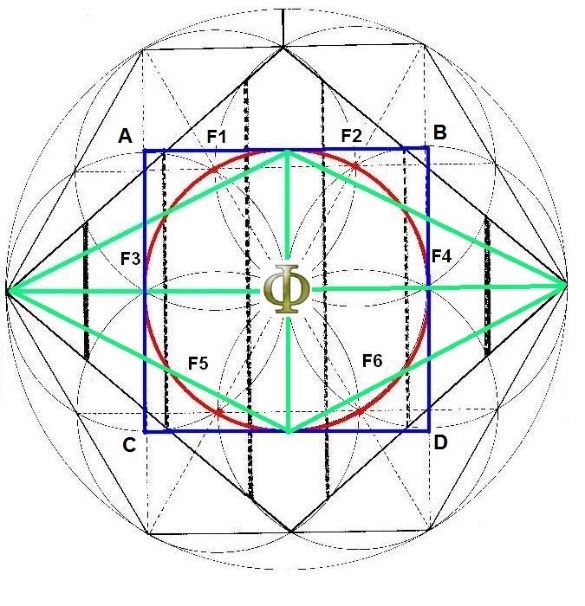
Figura. Phi en el Rombo

EL SUPER TRIÁNGULO

LA FUSIÓN DE DOS TRIÁNGULOS

Podemos imaginar que el Rombo surge de un entremezclamiento y de una fusión de dos triángulos energéticos que van el uno hacia el otro.

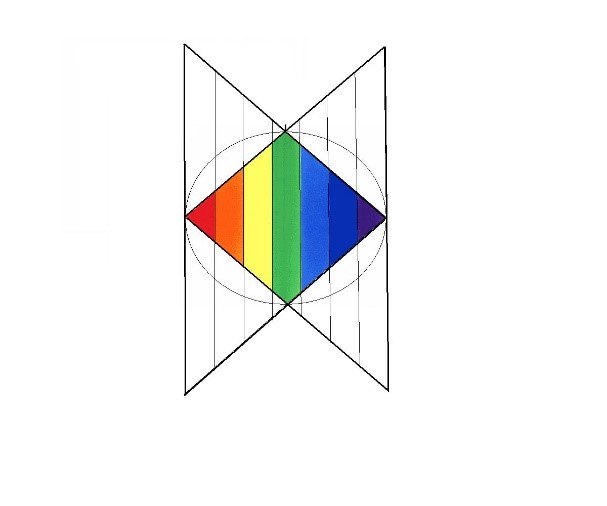
Figura. La fusión de dos triángulos

Partiendo de esta figura, nos vamos a centrar sólo en el triángulo que emerge desde la izquierda y a partir de aquí, empezaremos a estudiar el valor de las líneas y las áreas que se generan en este super triángulo.

LA MEDICIÓN DE LAS LÍNEAS

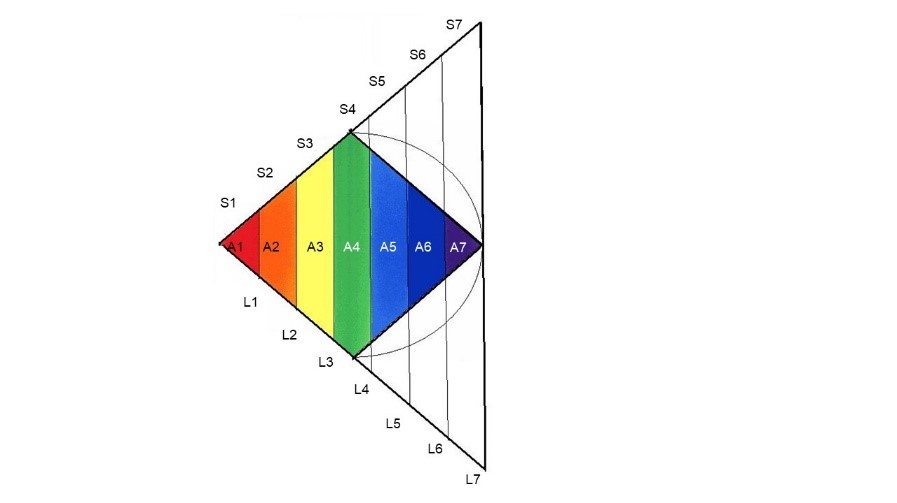
Figura. Áreas, Líneas y Superficies que aparecen en este super triángulo

Observamos en la figura un factor de crecimiento que se da en todas las líneas verticales del super triángulo. Si medimos los resultados obtenidos en la construcción geométrica de la figura, obtenemos las siguientes cifras, en las que vemos como el valor de cada línea dimensional del super triángulo, se obtiene multiplicando el número propio de la línea por 5.44, que es el valor por construcción de la línea inicial.

L1 L1 x 1 5.44

L2 L1 x 2 10.88

L3 L1 x 3 16.33

L4 L1 x 4 21.77

L5 L1 x 5 27.2

L6 L1 x 6 32.65

L7 L1 x 7 38.08

Podemos ver que el tamaño de una línea (L) está directamente relacionado con el orden en que va apareciendo y con el valor inicial de la primera línea hallada, que es 5.44.

Vemos también que el tamaño de una línea nueva es el de la línea anterior más el valor de la primera de las líneas. El crecimiento de las líneas se da en paquetes de 5.44. Es decir, el crecimiento de las líneas va de “paquete” en “paquete” o de cuanto en cuanto.

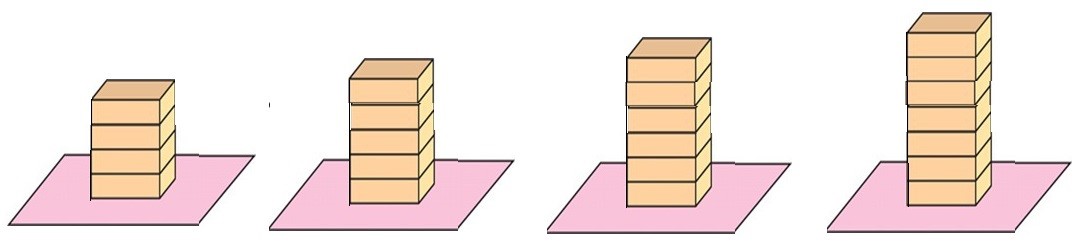
Figura. El incremento del valor de las líneas está cuantificado

LA MEDICIÓN DE LAS SUPERFICIES

Ahora vamos a medir las superficies generadas en este super triángulo. Los valores que matemáticamente obtenemos son los siguientes:

S1 8.54 x1 = 8.54

S2 8.54 x3 = 25.62

S3 8.54 x5 = 42.7

S4 8.54 x7 = 59.78

S5 8.54 x9 = 76.86

S6 8.54 x11 = 93.94

S7 8.54 x13 = 111.02

Donde vemos que la progresión de la medida de las superficies guarda una relación con la progresión 1.3.5.7.9.11.13.

LA MEDICIÓN DE LAS ÁREAS

Hemos hablado de Líneas y Superficies del Super triángulo, pero ahora vamos a hablar de las Áreas del Rombo. De la misma manera en que el valor las líneas ínter dimensionales se va incrementando en el super triángulo según una regla matemática, la superficie de las áreas correspondientes a las dimensiones pasa por un proceso parecido de crecimiento.

Para comprobar todo ello, podemos calcular las áreas de las superficies de las dimensiones. La anchura para todos los segmentos dimensionales es la misma: 22/7= 3.1428, y la altura de las líneas inter dimensionales por construcción es el que queda reflejado en la figura.

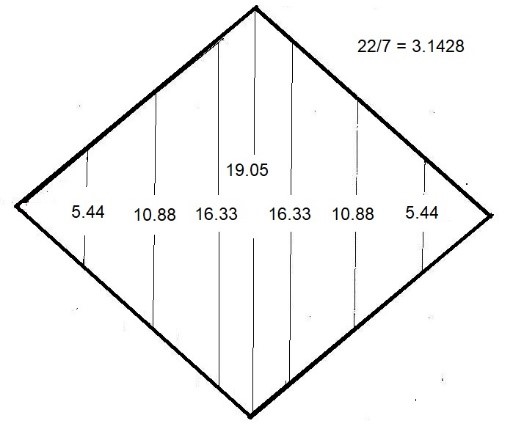
Figura. Figura del Rombo con medidas de las líneas

Vemos que la progresión del crecimiento de las áreas tiene lugar hasta llegar a la parte media de la 4ªD, donde el ascenso se detiene y se invierte, haciendo que, de este modo, se rompa la progresión que se había observado en las dimensiones previas. Con estos datos en la mano, vamos a calcular las áreas de todas las dimensiones.

Área 1ª dimensión: B x h = 5.44 x 3.14 = 8.54 cm²

Área 7ª dimensión: B x h = 5.44 x 3.14 = 8.54 cm²

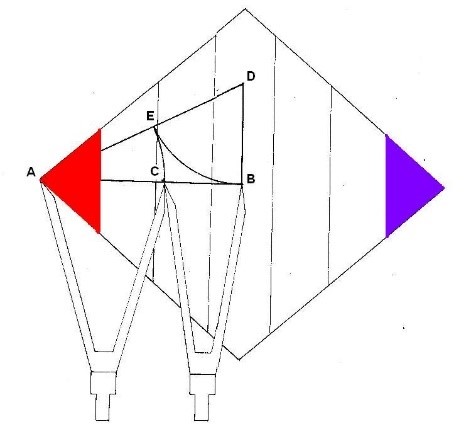
Figura. El área de la 1º y 7º dimensión

Y ahora vamos a calcular utilizando el mismo procedimiento matemático el área de la 2ª y 6ª dimensión:

Área 2ªdimensión: B + b x h = 10.88 + 5.44 x 3.14 = 25.62 cm²

2 2

Área 6ª dimensión: B + b x h = 10.88 + 5.44 x 3.14 = 25.62 cm²

2 2

Es decir, que en ambos casos el valor de la 2ªD y de la 6ªD, es el valor de la 1ªD multiplicado x3

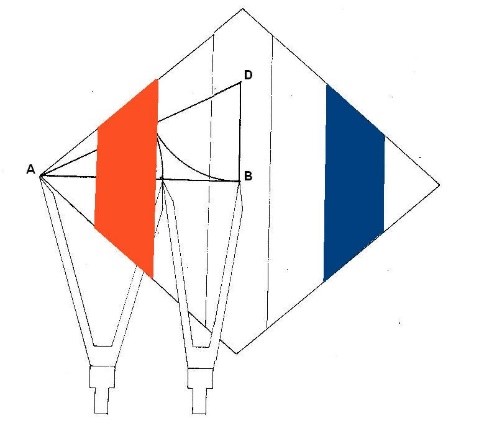
Figura. El área de la 2ª y 6ª dimensión

Y ahora lo mismo para las áreas de la 3ª y 5ª dimensión:

Área 3ªdimensión: B+b x h = 16.33 + 10.88 x 3.14 = 42.71 cm²

2 2

Área 5ª dimensión: B+b x h = 16.33 + 10.88 x 3.14 = 42.71 cm²

2 2

Es decir, el valor de la 3ªD y de la 5ªD es el valor de la 1ªD multiplicado por 5

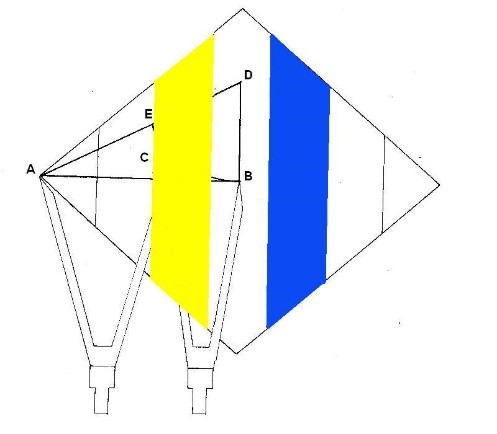
Figura. El área de la 3ª y 5ª dimensión

Pero en la cuarta dimensión ya no se cumple esta progresión 1,3,5,7 ya que sólo la primera parte de la 4ª dimensión es ascendente. La segunda parte es descendente. Esta área lógicamente no seguirá el mismo factor de crecimiento. Calculemos el área real de la 4ª D.

Área cuarta dimensión: B+b x h x 2 = 19.05+ 16.33 x 1.57 x 2 = 55.54 cm²

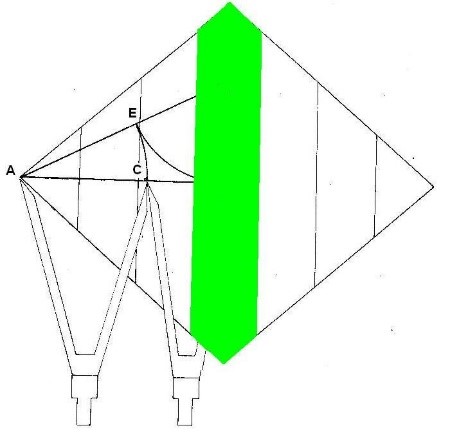
Figura. El área de la 4ª dimensión

Con estos datos, llegamos a unas conclusiones relevantes:

Las Líneas del super triangulo siguen unas leyes cuantizadas de crecimiento = 5.44 (x1, x2, x3, x4, x5, x6, x7)

Las áreas de las Superficies del super triángulo también siguen una fórmula cuantizada de crecimiento = 8.54 (x1, x3, x5, x7, x9, x11, x13)

Las áreas de las dimensiones del Rombo también crecen cuantizadas = 8.54 (x1, x3, x5) hasta que llegan a la cuarta dimensión, donde esa progresión se pierde ya que una parte es ascendente y la otra es descendente. A partir de la mitad de la 4ª D, la progresión de crecimiento se invierte (x5, x3, x1)

La idea del super triángulo bidimensional abre la posibilidad a la representación del super triángulo tridimensional o lo que es lo mismo a tener la posibilidad de llegar a tener en las manos una nueva perspectiva del Rombo. Después del Rombo bidimensional, llega el Rombo tridimensional, que es de lo que tratará el siguiente capítulo.

LA FLOR DE LA VIDA

INTRODUCCIÓN

La Flor de la Vida es el nombre por el que se conoce recientemente a un dibujo que se encuadra dentro de la familia de las figuras geométricas consideradas sagradas porque gracias a su lenguaje simbólico transmiten información relevante acerca del origen de la vida, de su ordenamiento e interconexión. Este dibujo ha sido empleado desde la remota antigüedad en todo el mundo, en épocas y culturas muy diferentes como un símbolo de las leyes universales.

Está formada por 19 círculos completos del mismo diámetro que están enmarcados dentro de un hexágono y una circunferencia. Los círculos crean al fusionarse patrones simétricos y ordenados que forman un conjunto armónico que recuerda a la forma de las flores.

Su geometría forma una red que representa la unidad del todo y muestra como todas las distintas manifestaciones de la existencia, por más alejadas que estén las unas de las otras, están interconectadas y regidas por el mismo principio creador.

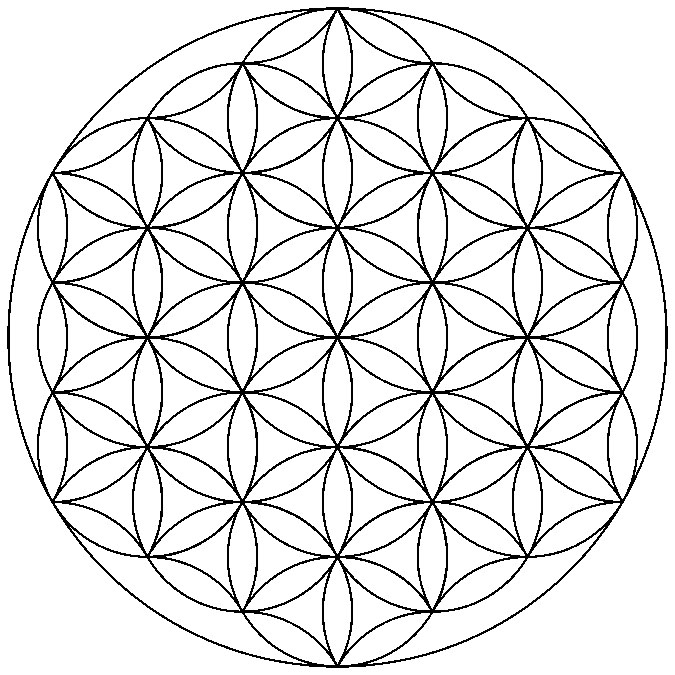
Figura. La geometría sagrada de La Flor de la vida

Al encontrarse presente en lo grande y en lo pequeño, se dice de este símbolo que contiene todas las manifestaciones del universo, todas las leyes físicas, las matemáticas, la armonía de la música, y las distintas expresiones de la vida biológica y atómica. Es también el patrón del amor, de la armonía, la coherencia, la interconexión, la integración y la información infinita que se da en todos los lugares de la existencia.

A esta figura, conocida también como roseta hexapétala, se la ha considerado también como un símbolo de los ciclos de la vida por la circunferencia que la envuelve, como el centro del origen de todo, el punto de partida, el de llegada, la inmortalidad y la luz eterna de Dios.

UN HALLAZGO GEOMÉTRICO: LOS FOCOS Y LAS MARGARITAS

En el año 2.000 y cuando aún no sabíamos de la existencia del dibujo conocido como la Flor de la Vida, buscando datos matemáticos relacionados con los valores de la diagonal menor dentro de la geometría interna del Rombo, realizamos un dibujo en el que se veía como dentro del Hexágono y del Rombo aparecían unas líneas onduladas a las que, en su día llamamos margaritas.

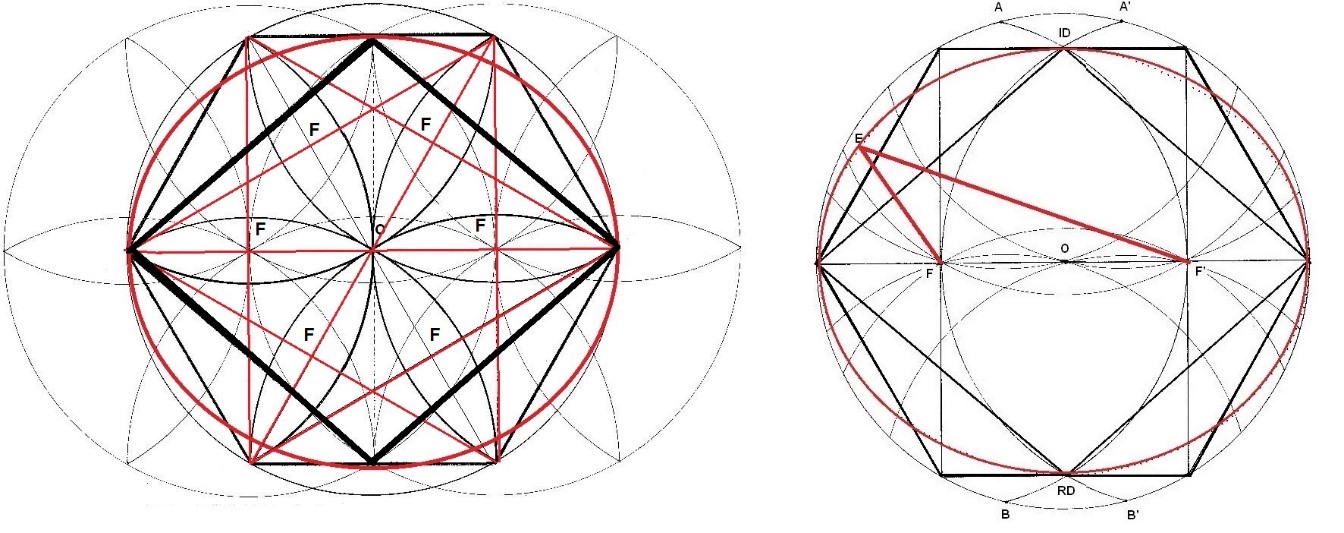
Figura. Las margaritas del Rombo y los Focos de la elipse

En este dibujo, que inscribía al Rombo dentro de un hexágono y un círculo, aparecía un Rombo cuyos valores de la diagonal mayor eran de 22 cm y los de la diagonal menor eran de 19.05… Aparte de este dato, que era de sumo interés y que podía esclarecer un dilema acerca de las posibles medidas de la diagonal menor del Rombo, aparecieron dos puntos geométricos muy importantes, que eran los Focos de la elipse (F) y que se encontraban en el punto medio de los pétalos horizontales de la margarita central. Estos puntos eran los que permitían dibujar a la elipse que circunscribía al Rombo utilizando el método tradicional del jardinero.

En los dibujos, observamos que aparecían también dos margaritas que parecían tener una parte fuera del Rombo y que sobresalían por la derecha e izquierda. En el centro de estas margaritas, se hallaban los Focos (F). Estos Focos, estaban situados en el punto central de las margaritas exteriores y al mismo tiempo, en el punto medio de las hojas derecha e izquierda de la margarita central.

En el centro del hexágono se podía ver una gran margarita central, que ocupaba todo el hexágono exterior y cuyo centro era el punto (O).

Y además de este dibujo en el que se veía esta gran margarita ubicada en el centro y que ocupaba todo el hexágono exterior, en un dibujo posterior, un poco más elaborado, se podía observar otra margarita central, más pequeña, que contactaba con el hexágono interior, y que aparecía cuando se hacían 7 círculos cuyo centro era cada uno de los 6 Focos y el punto central O.

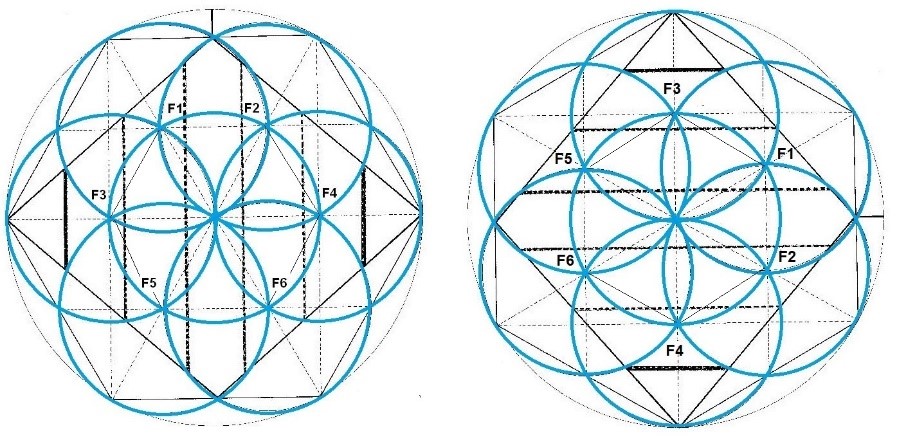
Figura. Dos Rombos a 90º. La margarita central pequeña y las dimensiones

El radio que permitía dibujar a estos círculos pequeños era la mitad del radio con el que se había dibujado la circunferencia exterior y el hexágono.

Este dibujo fue crucial para poder empezar a entender la geometría interna de la figura, ya que las líneas de contacto de cada una de las circunferencias pequeñas con las líneas exteriores del Rombo, generaba unas marcas en la parte superior e inferior del Rombo. Entonces sólo había que unir estos dos puntos de intersección y aparecían dibujadas las 6 líneas verticales que formaban las 7 dimensiones del Rombo.

LA RELACIÓN DEL ROMBO CON LA FLOR DE LA VIDA

En aquel momento, no lo supimos ver, pero ahora podemos observar una exactitud geométrica y matemática entre el dibujo de la pequeña margarita central del Rombo y lo que se conoce como la semilla de la vida (que es la parte central de la Flor de la Vida), una figura hecha con los mismos 7 círculos entrelazados que se encuentran también en la geometría interna del Rombo.

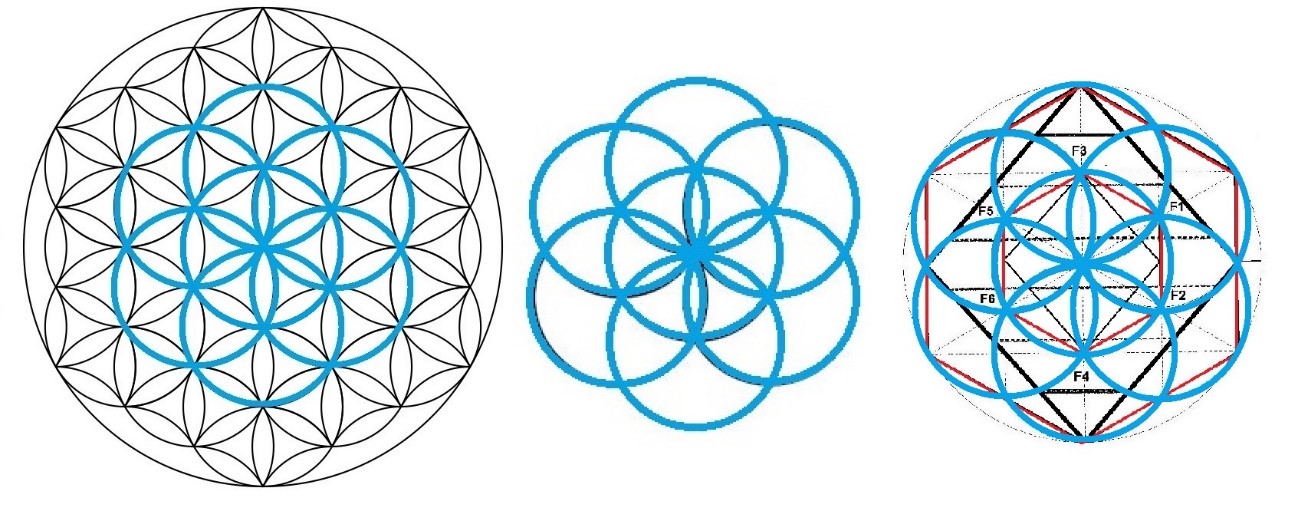
Figura. La Flor de la vida, la semilla de la vida y el Rombo

En aquellos primeros dibujos del Rombo, pudimos observar que las margaritas estaban presentes dentro de todo el tejido del Rombo y que podían aparecer de muchas maneras, dependiendo desde donde se trazaran las circunferencias. Esa estructura floreada no tenía una única manifestación. Al contrario, parecía un dibujo imposible de acabar porque el patrón geométrico de las flores aparecía de una manera u otra según se estudiara un aspecto determinado. Además, el dibujo podía ofrecer también una ilusión óptica consistente en el sentido de que las margaritas parecían desplazarse de izquierda a derecha, de arriba a abajo o en diagonal. Con todas estas observaciones, vimos en aquel momento que había ciertamente una relación directa entre la presencia de las margaritas y la estructura interna de la Sagrada Forma del Rombo.

Al mismo tiempo, y según observamos ahora, no parece existir una línea temporal única en la creación de una figura o de otra, ya que, si se parte de la circunferencia, del hexágono y de las circunferencias centrales, se puede construir el Rombo con sus dimensiones, pero si se empieza desde el mismo Rombo, se puede construir el hexágono, la circunferencia y las circunferencias centrales. Ambas figuras están unidas y se autogeneran y alimentan. Una es el sustento de la otra y viceversa.

En nuestro estudio, la figura inicial fue la circunferencia, y de ella nació el hexágono y el Rombo. Y estudiando la geometría del hexágono aparecieron los Focos, las margaritas y por último las dimensiones. Pero en la actualidad es posible reconstruir todo este rompecabezas siguiendo otro orden. No se puede decir con claridad que una de las dos figuras (el Rombo o la Flor) sea anterior a la otra y la genere. Parece que una crea a la otra y viceversa, o que la generación de las figuras tiene dos puntos de creación de distinto sentido que confluyen en una misma línea temporal.

EL CRECIMIENTO DE LAS MARGARITAS

En los primeros dibujos, se podía ver una aparente movilidad de las margaritas, pues éstas, podían desplazarse por el Rombo y formar una especie de trenzas en su desplazamiento y muy lejos de aparentar quietud, la imagen de las margaritas sugería la idea de desplazamiento y de movilidad horizontal, vertical y diagonal.

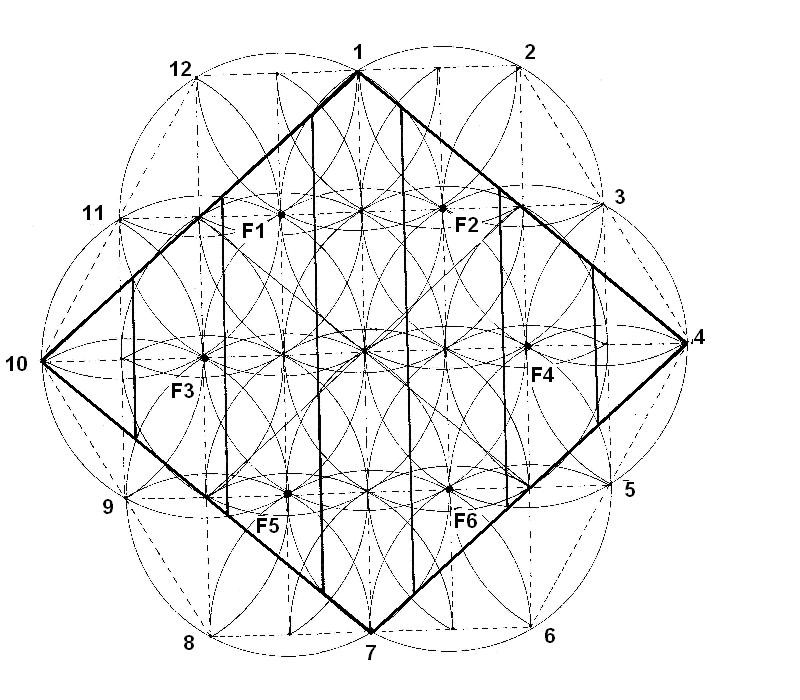
Figura. Las trenzas de margaritas horizontales

Vimos que las margaritas estaban dentro del Rombo y que éstas podían salir de él, expandirse mucho más allá de sus límites y formar un mosaico que se repetía continuamente y que tenía una cadencia y un orden muy armónico.

En aquel momento, se optó por hacer un estudio para observar ese mosaico y la progresión del número de margaritas (1,2,3,4,5,6) dentro de un triángulo equilátero para poder observar su crecimiento. Vimos que el mosaico podía ser infinito y que repetía continuamente la presencia de los 6 focos hallados en la geometría interna del Rombo. Vimos entonces que el mosaico estaba lleno de Rombos que se interconectaban los unos con los otros en un patrón que se repetía hasta el infinito. El Rombo, junto con las margaritas y los Focos, formaban un conjunto indisoluble que se propagaba en todas las direcciones de espacio y tiempo.

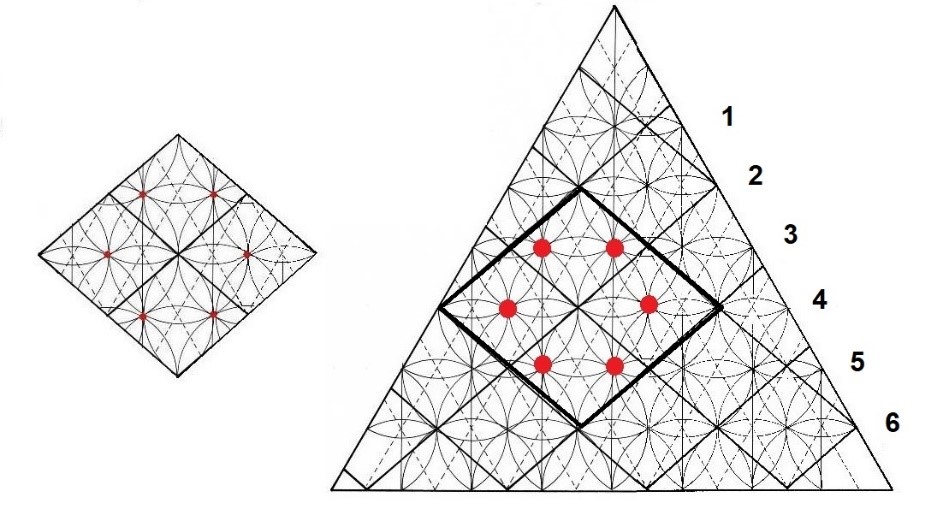
Figura. El crecimiento infinito del Rombo y las margaritas

El dibujo del triángulo permitía dar continuidad al mosaico y sólo hacía falta unir más triángulos para que Los Rombos y las margaritas se pudieran expandir más en todos los sentidos y originar una figura más amplia. El patrón de las margaritas se podía dilatar sin límite alguno en todas las direcciones del espacio tridimensional y podía ser delimitado por cualquier figura geométrica sobre la que se quiera realizar el estudio.

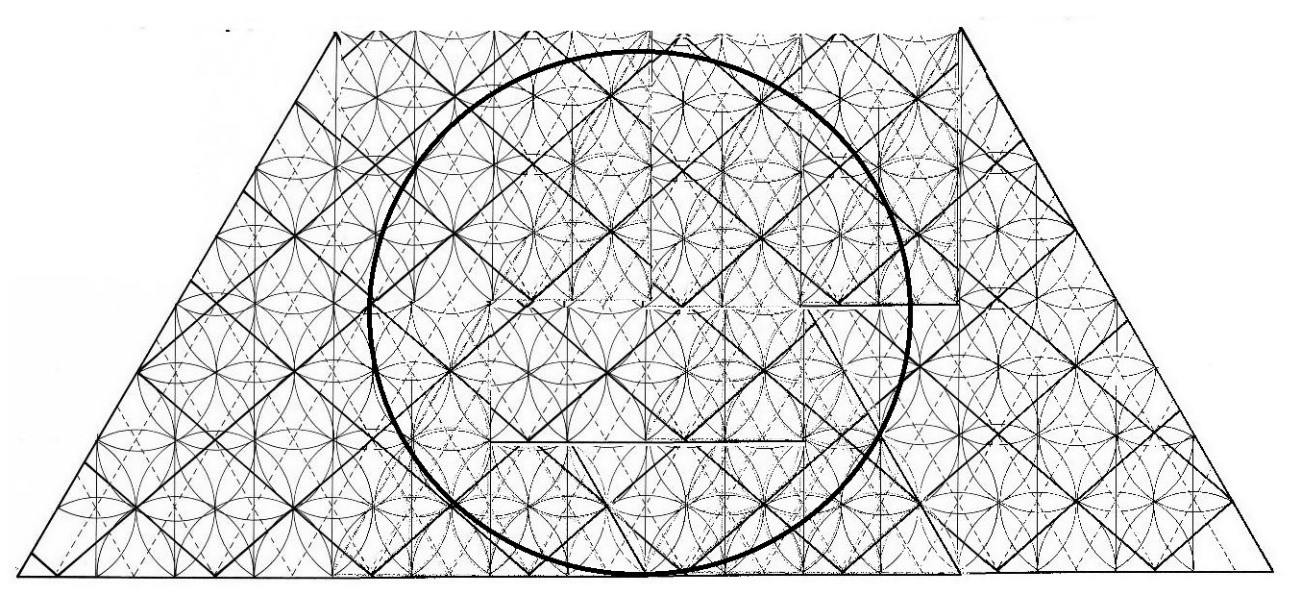
Figura. La unión de los triángulos da un mosaico más amplio.

En la actualidad, al haber conocido a la figura de la Flor de la Vida, hemos podido ver que lo que en aquel momento se dibujó, toda esa serie de Rombos y margaritas alineadas, tiene la misma disposición geométrica que la que se halla en la llamada Flor de la Vida.

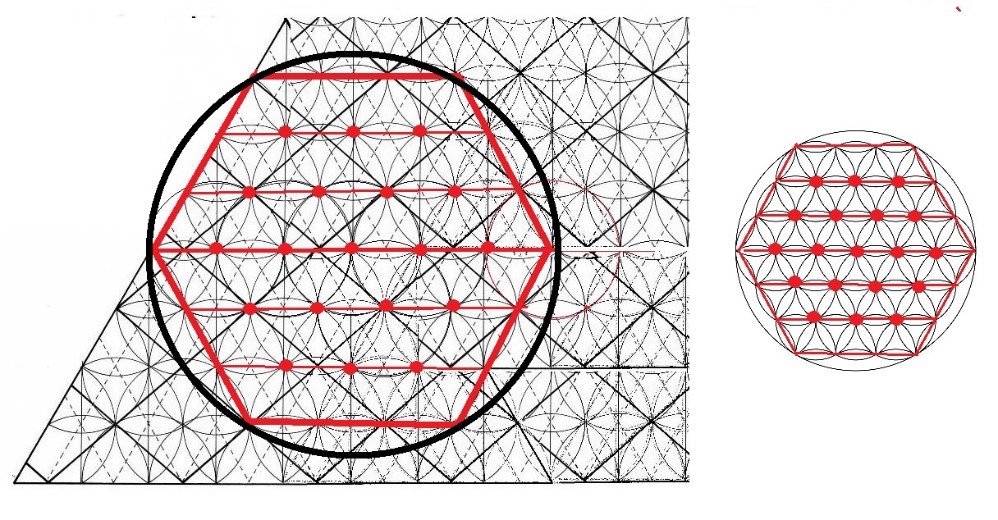
Figura. La misma geometría está en las margaritas y en la flor de la vida

En aquella época, experimentamos mucho más acerca de las posibilidades geométricas que se hallaban dentro del Rombo, y observamos como toda esa perfección y belleza de formas, nos llevaba a la conclusión de que el valor hallado de 19.05... para la diagonal menor, (que era un dato sobre el que teníamos muchas dudas y que nos había llevado a hacer este trabajo geométrico) tenía que ser un valor posible por puras cuestiones de construcción geométrica. Era impensable que tanta belleza y armonía no significaran nada y que la cifra hallada para la diagonal menor no fuera un valor posible ya que formaba parte esencial en la estructura de ese patrón armónico. De hecho, el estudio geométrico que se había puesto en marcha en busca de un valor posible para la diagonal menor finalizó con este hallazgo y con esta conclusión.

LA GEOMETRÍA SAGRADA

Como consecuencia del estudio, surgieron de una manera colateral muchas otras figuras vinculadas con este tipo tan especial de geometría. En su día, no se estudiaron en profundidad porque ya se había encontrado el dato que se buscaba, y todos los demás hallazgos quedaron clasificados como descubrimientos secundarios y no abrieron un camino de estudio por el que se debiera transitar en aquel momento.

En cualquier caso, el adentrarnos en la geometría interna del Rombo, nos abrió las puertas a un mundo de conocimientos y sorpresas de lo más agradable y enriquecedor. Todos los bellos dibujos y los hallazgos que surgieron decían que la geometría interna del Rombo era infinita y que expresaba unos conceptos primordiales y sagrados acerca del origen de la vida, de su orden interno y su interconexión. Las ideas filosóficas del Rombo podían ser expresadas en palabras, pero el lenguaje que se utilizaba en este caso y bajo la forma de la geometría era más sintético, simbólico y universal.

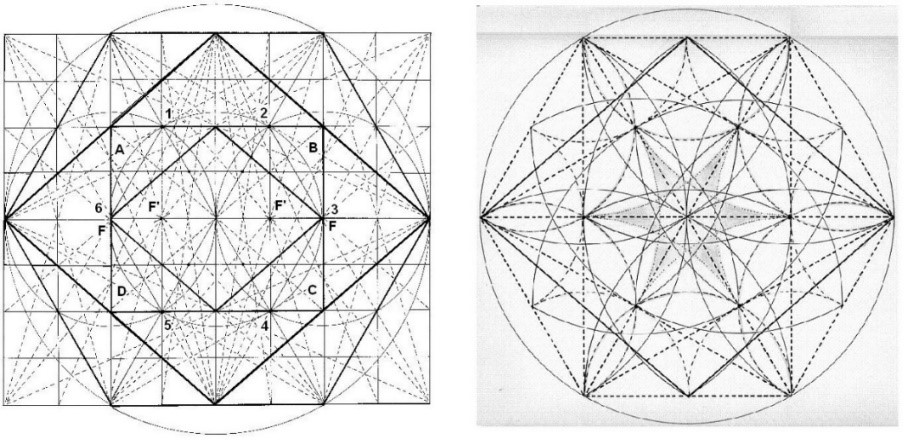
Figura. Las líneas y la estrella dentro del Rombo

Habíamos empezado con un juego de compás que bailaba y daba vueltas a ciegas buscando puntos de intersección con otras líneas (ya fueran lineales o circulares) y habíamos finalizado con un descubrimiento vital, con el hallazgo de unas propiedades y de una geometría interna sorprendente.

Y es que cuando se parte de una figura sagrada como es la circunferencia, con un poco de curiosidad, de imaginación y de tiempo, se pueden llegar a encontrar muchas otras figuras. Esto es seguramente lo que les sucedió a las personas que estudiaron la Flor de la Vida y que encontraron en el camino a otras figuras que están en su línea, como son la semilla de la vida y el fruto de la vida.

La misma figura del fruto, puede evolucionar a otras más complejas si se trazan líneas que unan las circunferencias. Aparece entonces otra figura que recibe el nombre de Metatron, en la que se adivina la presencia de los 5 sólidos platónicos.

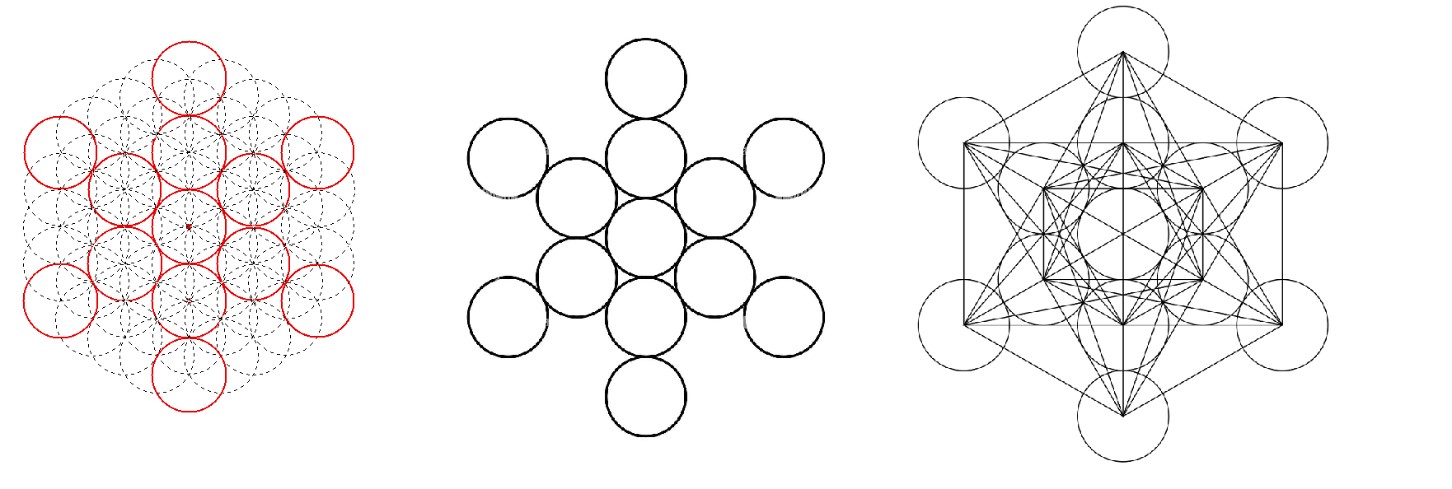
Figura. El fruto de la vida y Metatron

EL ROMBO Y LA FLOR DE LA VIDA

Si profundizamos un poco en el estudio de la Flor de la Vida, veremos que está enmarcada por una circunferencia exterior que contiene tres hexágonos paralelos y concéntricos.

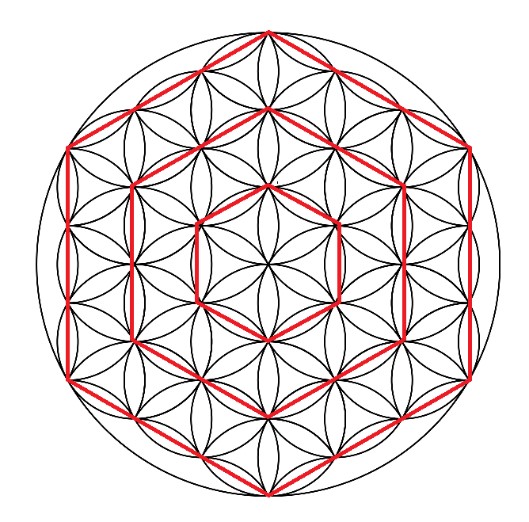
Figura. Los hexágonos de la Flor de la vida

Se puede observar como la creación de los tres hexágonos tiene lugar uniendo los puntos centrales de las margaritas que están alineadas.

En la figura siguiente, nos vamos a centrar en el primer y el segundo hexágono contando desde el interior y vamos a comparar el dibujo resultante con el que ofrece el Rombo.

Vemos como dentro del dibujo de la Flor de la Vida, en el hexágono interior, se observan los 6 puntos de las margaritas que contactan con los vértices del hexágono. A su derecha observamos el dibujo de la semilla de la vida, con los hexágonos y el Rombo. Y en el dibujo que está más a la derecha, aparecen los mismos puntos ya dentro del Rombo y que reciben el nombre de Focos: (F1, F2, F3, F4, F5, F6) que contactan también con el hexágono interior y que permiten construir las dimensiones del Rombo dibujado en negro.

Los hexágonos interiores y exteriores de las tres figuras son los mismos, y en todos ellos se puede dibujar un Rombo.

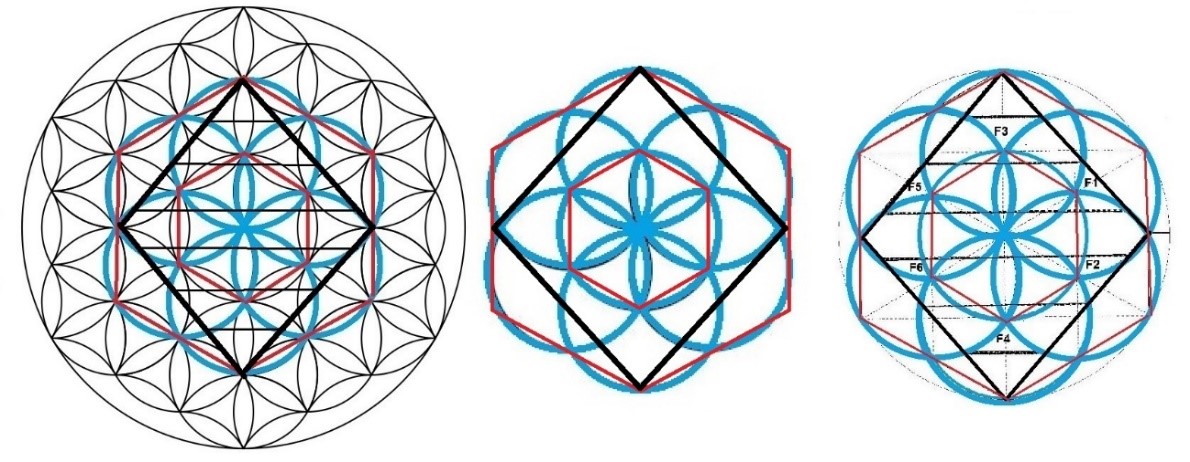
Figura. La flor de la vida, la semilla de la vida y el Rombo

Desde el hexágono pequeño y los vértices de las margaritas que contactan con él, se puede construir al Rombo que se enmarca en el hexágono siguiente, el mediano. De este hecho, parece surgir la idea de que para construir algo grande, se ha de partir de un principio que es previo, menor y necesario.

Si nos centramos en el hexágono del medio (en el que se inscribe el Rombo), observaremos que, por fuera del hexágono, se construye la circunferencia que contacta con el hexágono en cada uno de sus vértices y que, a su vez, contacta con el centro de las margaritas cada dos encuentros con ellas.

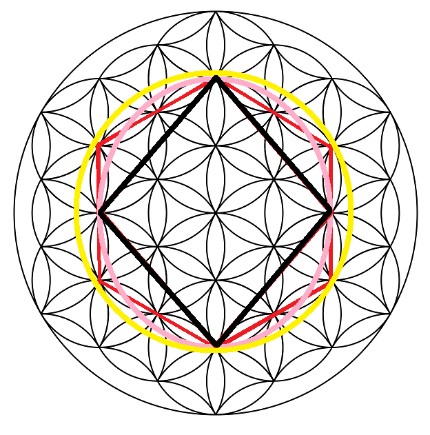
Figura. Las margaritas y su relación con la circunferencia y la elipse

La elipse corre por fuera y por dentro del hexágono y contacta con el centro de las margaritas en ciclos de 3 encuentros. Estas dos figuras circulares y que están totalmente unidas al Rombo, necesitan también como vemos, la presencia de las margaritas para su construcción. Tal como observamos, todos los elementos del Rombo necesitan para su construcción la presencia de estas flores.

Sino queremos dejar el hexágono exterior de lado en este estudio, podemos prestarle un poco de atención y observar que sucede con él. Podemos superponer la figura del Rombo con la semilla de la Vida incluida sobre la figura de la Flor de la Vida de manera que coincidan los hexágonos exteriores y veremos como también el Rombo se puede construir perfectamente sobre este tercer hexágono. Lo que sucede es que la margarita central, los Focos y el Rombo se han de expansionar. El único punto que no se mueve en la expansión es el centro, como es lógico desde un punto de vista metafísico, pues el centro es inamovible y permanece estable. Todas las demás estructuras se han de dilatar manteniendo sus proporciones para llegar hasta tercer hexágono.

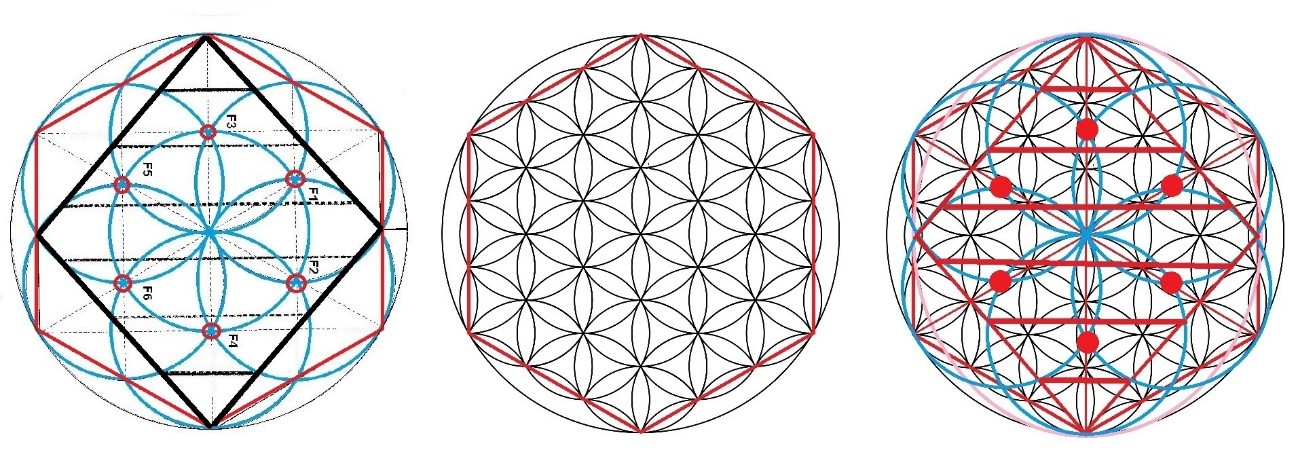
Figura. El Rombo sobre el tercer hexágono

El Rombo dentro del tercer hexágono, lo podemos construir por traslación directa desde la semilla de la vida o haciéndolo de nuevo a través de sus focos. Para ello, primero dibujamos el tercer hexágono. A continuación, encontramos los focos uniendo los vértices no contiguos del hexágono.

En el resultado final del dibujo, vemos que los Focos (marcados como esferas en rojo) no se sitúan en el centro de las margaritas que forman la trama de la Flor, sino en puntos intermedios.

Vemos que, para construir un Rombo enmarcado en el hexágono exterior, no sirven como punto de referencia los Focos de las margaritas pequeñas. En este caso, se ha de partir de la margarita pequeña central y expansionarla, dilatarla hasta que tenga la medida exacta para poder construir el Rombo y sus dimensiones.

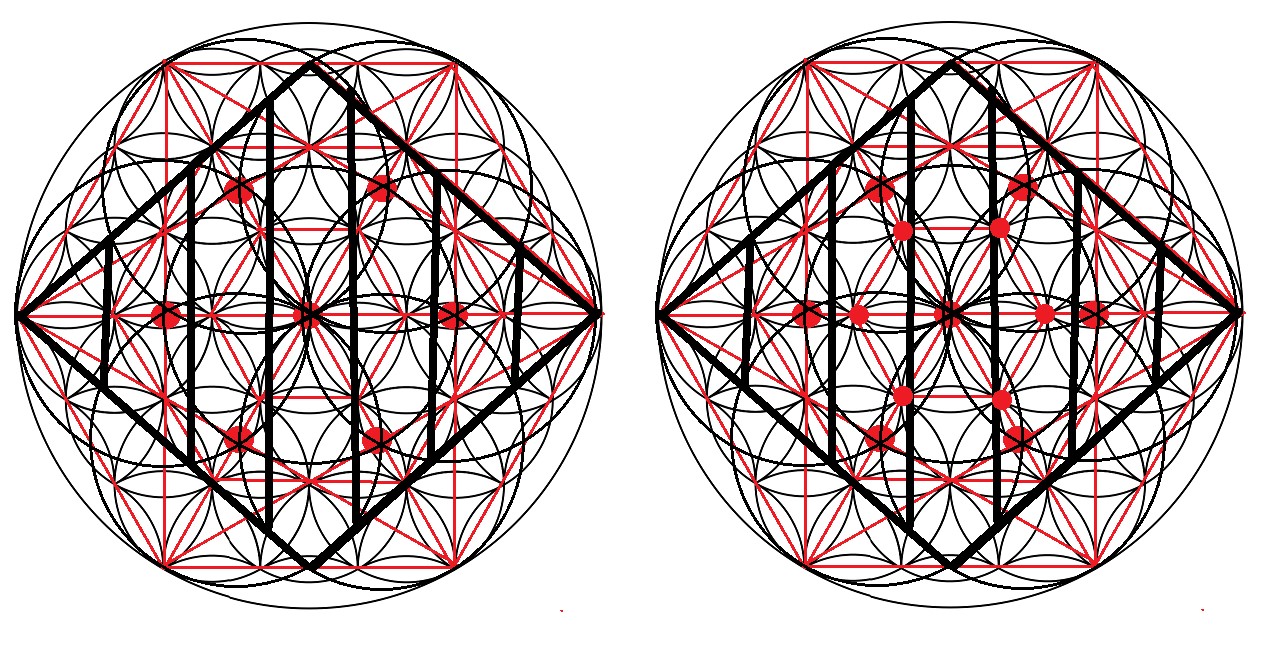
Figura. La construcción del Rombo en el tercer hexágono

Hay en el diseño de la Flor de la Vida un dato relevante y que se ha de considerar. Por algún motivo, el dibujo expansivo de la flor de la vida se detiene en un momento determinado (en el tercer hexágono) y no se permite que el último círculo de margaritas se exprese con totalidad, ya que la circunferencia exterior secciona por la mitad a la última fila de estas y sólo permite la expresión de la mitad del dibujo de las margaritas que forman la última hilera de flores. En cambio, la geometría repetitiva de la figura permite seguir indefinidamente esta expansión que nace desde el centro, lo que hace posible que podamos dibujar un cuarto hexágono y Rombo.

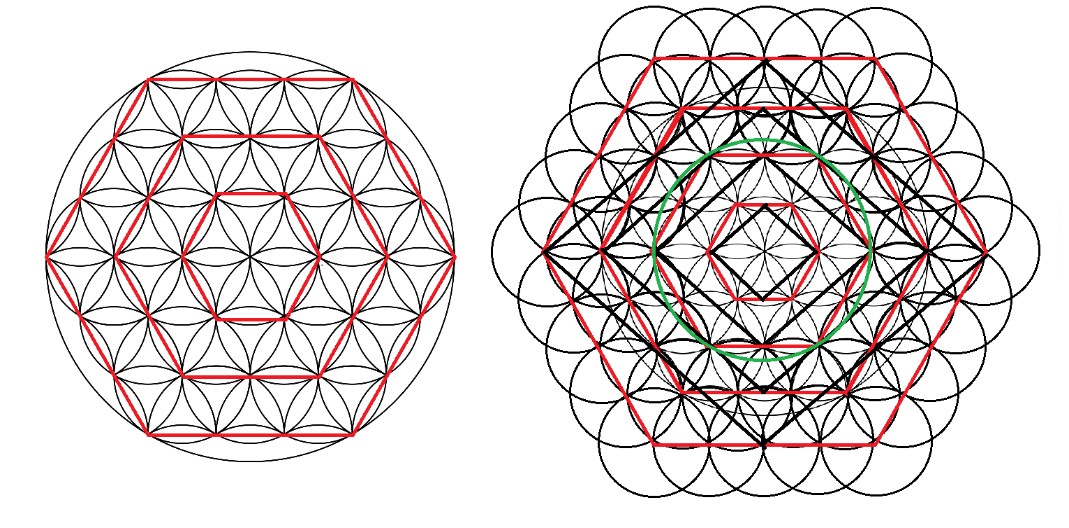
Figura. El cuarto hexágono

La Flor de la Vida permite ir añadiendo hexágonos exteriores y poder ir dibujando en ellos, distintos Rombos, cada vez mayores. El proceso geométrico es algo complejo y elaborado, pero se pueden ir construyendo Rombos sobre los que, por geometría interna, a través de los Focos, se pueden ir creando las 7 dimensiones.

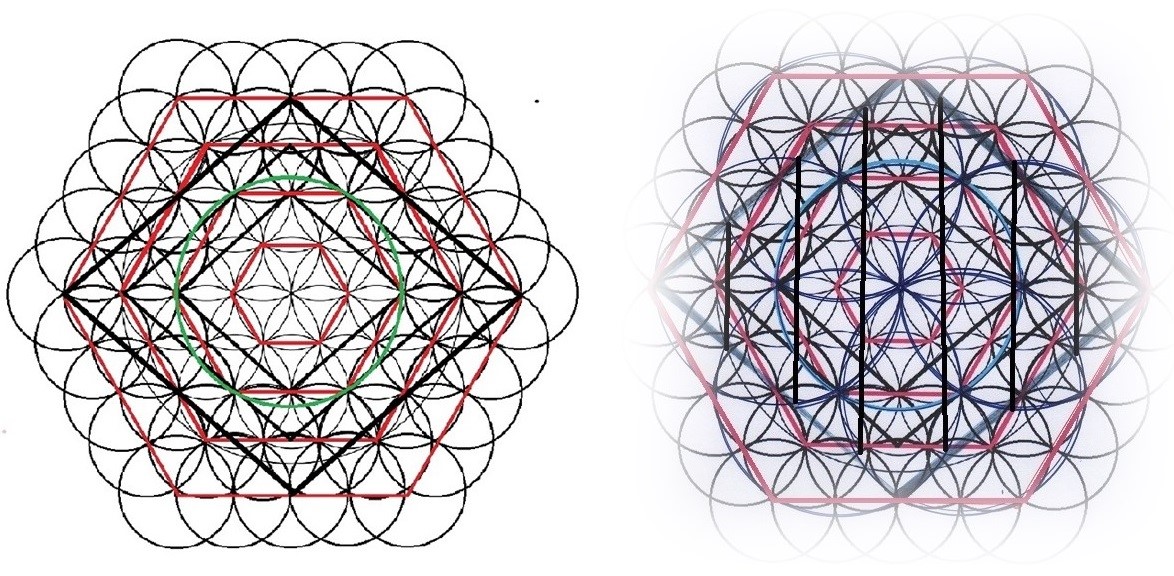
Figura. El cuarto hexágono y el Rombo interior.

Esto no hace más que recordar el hecho de que el Rombo se puede hallar en un hexágono pequeño, en uno mediano o en uno grande. Al dilatarse él, se mueve al mismo tiempo toda la estructura de la Flor de la Vida, pues es un arquetipo que permite la expansión o la contracción, ir hacia adentro o hacia afuera ya que se adapta a todos los tamaños, pudiendo manifestarse en lo microscópico o en lo macroscópico. El Rombo y la Flor bailan juntos y se contraen y expanden al mismo tiempo. Uno forma parte del otro y lo necesita. Son simbióticos.

Ambas figuras parecen dar la sensación de que mientras uno es el soporte inmaterial que lo abarca todo, el otro es la estructura firme que permite la concreción y la manifestación física de la vida.

CONCLUSIONES

Todos estos dibujos revelan como la estructura que subyace, soporta y sobre la cual se construye el Rombo es el conjunto geométrico de margaritas conocido como la Flor de la Vida. Toda la construcción de los elementos internos y externos que forman la estructura del Rombo se hace sobre la necesaria presencia de esta trama geométrica que abarca el espacio en todas sus infinitas direcciones y dimensiones.

Si este invisible tejido energético está en todos los recovecos del Rombo, es lógico pensar que todas las cualidades que se le atribuyen a la Flor de la Vida (patrón universal, coherencia, integración, interconexión, holografía, armonía, información infinita, eternidad y amor) estén presentes también en el Rombo. Y además el Rombo nos aporta todo el contenido de los conceptos albergados en él y que no se observan directamente en la flor de la vida: Yin-Yang, Rayos, elementos primarios, Ideación Divina, dimensiones, planos de conciencia, ciclos, holografía, movimiento armónico simple, movimiento circular uniforme, espacio interestelar, esfera generadora de energía, estructura Divina, leyes físicas de la luz y el conocimiento de las leyes evolutivas que permiten al ser humano convertirse en una criatura ascendente cósmica.

Todo ser evolucionado del universo llega a este conocimiento ancestral de la Flor de la Vida cuando le llega la hora en que su evolución mental y espiritual le llevan a un nivel que le permiten conocer y sentir el significado de este sagrado símbolo. Y al lado de la Flor de la Vida, formando parte de ella también y aportando un contenido extra de conceptos y riqueza, está la figura de la Sagrada Forma del Rombo, una figura construida sobre arquetipos sagrados y que pone de manifiesto verdades universales que expresan todo su contenido a través del lenguaje de la geometría sagrada. Ambas crean la Unidad en la dualidad.

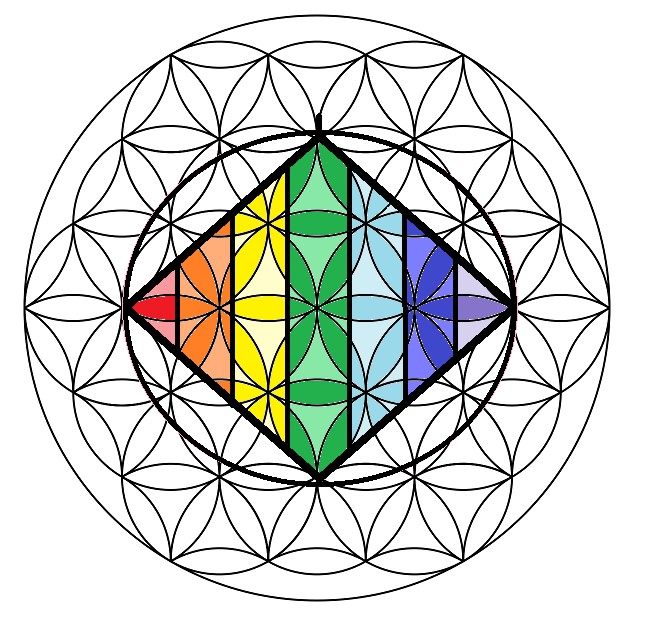
Figura. La SFR y la Flor de la vida

Apartados SFR

La figura bidimensional del Rombo